Алгоритмы построения обратной матрицы
1. Вычислим 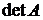 и убедимся, что он не равен нулю. Это будет означать, что существует
и убедимся, что он не равен нулю. Это будет означать, что существует 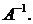
2. Построим так называемую присоединенную матрицу 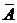 . Для этого алгебраические дополнения элементов, расположенных в строках данной матрицы А, поместим в столбцы с соответствующими индексами, т. е. присоединенная матрица имеет вид:
. Для этого алгебраические дополнения элементов, расположенных в строках данной матрицы А, поместим в столбцы с соответствующими индексами, т. е. присоединенная матрица имеет вид:
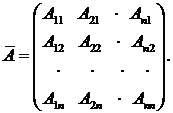
3. Составим матрицу 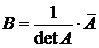 и проверим, что
и проверим, что 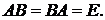 Это означает, что мы построили обратную матрицу
Это означает, что мы построили обратную матрицу 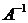 . Итак,
. Итак, 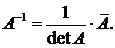
Свойства обратной матрицы
1. 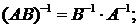 2. (
2. ( 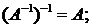
3. 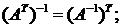 4.
4. 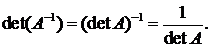
Решение матричных уравнений
С помощью обратной матрицы легко решаются матричные урав-нения вида АХ = В (1) или УА = В (2), где А и В – данные матрицы,
det А ¹ 0, Х, У – неизвестные матрицы:
1) 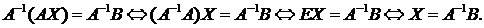
2) 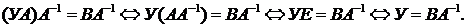
Пример. Решить матричное уравнение 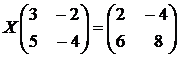 или
или 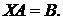
Решение. Если 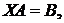 то
то 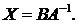
Определим 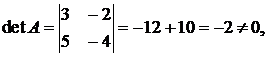 значит, существует обратная матрица
значит, существует обратная матрица 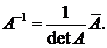 Найдем
Найдем 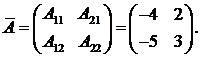
Итак, 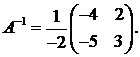 Следовательно,
Следовательно, 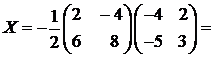
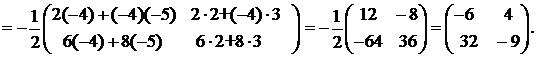
Системы линейных уравнений
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Систему уравнений вида 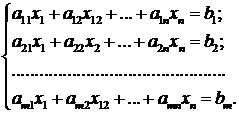 (2.1)
(2.1)
называют системой m линейных уравнений с n неизвестными. Коэффициенты при неизвестных 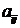 образуют матрицу
образуют матрицу 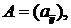 где
где 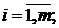
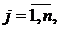 которая называется основной матрицей системы. Если эту матрицу дополнить столбцом свободных членов
которая называется основной матрицей системы. Если эту матрицу дополнить столбцом свободных членов 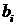 , то получится расширенная матрица
, то получится расширенная матрица 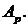
Решением системы называется любое множество чисел
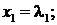
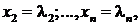 которые обращают каждое уравнение системы
которые обращают каждое уравнение системы
в тождество.
Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая решений, называется несовместной. Совместная система может иметь одно или множество решений. Система, имеющая единственное решение, называется определенной, и неопределенной, если она имеет более одного решения.
Линейная система (2.1) называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, то такая система называется однородной. Однородная система всегда совместна, т. к. она всегда имеет нулевое решение.
Исходя из геометрического толкования линейного уравнения с двумя и тремя неизвестными соответственно следует:
1) решение системы двух линейных уравнений с двумя неизвестными есть точки пересечения прямых, заданных соответствующими уравнениями системы. Причем:
– 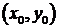 – единственная точка пересечения прямых, если система имеет единственное решение;
– единственная точка пересечения прямых, если система имеет единственное решение;
– множество точек (прямые совпадают), если система имеет бесчисленное множество решений;
– нет точек пересечения (прямые параллельны), если система несовместна.
2) с геометрической точки зрения единственное решение системы трех линейных уравнений с тремя неизвестными означает, что плоскости пересекаются в одной точке 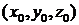 ;
;
3) однородная система всегда совместна, т. к. каждая плоскость (прямая), уравнение которой не содержит свободного члена, проходит через начало координат и, значит, х = 0, у = 0, z = 0 всегда является решением однородной системы.
Две системы называются эквивалентными или равносильными, если любое решение одной из них является также решением другой и наоборот, т. е. если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Решить систему уравнений – это значит выяснить:
1) совместна она или несовместна;
2) в случае совместности – найти все ее решения.
ПРАВИЛО КРАМЕРА
Если число n неизвестных системы линейных уравнений (2.1) совпадает с числом m уравнений, т. е. n = m, то существует определитель 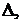 элементами которого являются коэффициенты при неизвестных. Этот определитель называется главным определителем системы. Обозначим через
элементами которого являются коэффициенты при неизвестных. Этот определитель называется главным определителем системы. Обозначим через 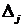 определитель, получающийся из главного определителя
определитель, получающийся из главного определителя 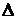 заменой j-го столбца столбцом свободных членов, и назовем его вспомогательным. Например, вспомогательные определители
заменой j-го столбца столбцом свободных членов, и назовем его вспомогательным. Например, вспомогательные определители
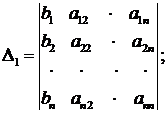
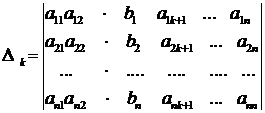
Теорема Крамера. Если главный определитель системы 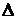 отличен от нуля, то система имеет единственное решение:
отличен от нуля, то система имеет единственное решение:
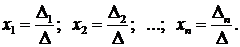
Следствия.
1) Если главный определитель и все вспомогательные определители системы равны нулю, то система имеет бесчисленное множество решений.
2) Если главный определитель системы равен нулю, но хотя бы один из вспомогательных определителей отличен от нуля, то система несов-местна.
Пример. Решить систему уравнений 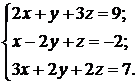
Решение. Найдем главный и вспомогательные определители системы:
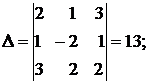
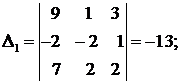
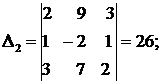
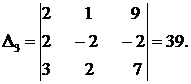
Так как 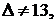 то система имеет единственное решение:
то система имеет единственное решение:
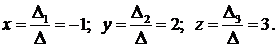
С геометрической точки зрения полученное решение означает, что три плоскости, заданные соответствующими уравнениями системы, пересекаются в единственной точке