Проверка адекватности однофакторной регрессионной модели
Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным.
Адекватность регрессионной модели при малой выборе можно оценить F критерием Фишера:
,
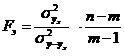где m – число параметров модели;
n - число единиц наблюдения;
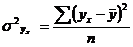- факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака фактора, включенного в модель;
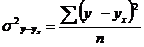- остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих, неучтенных факторов;
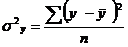- общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию:
.
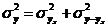Эмпирическое значение критерия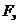 
сравнивается с критическим (табличным) 
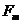с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m).
Если 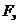> 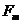, то уравнение регрессии признается значимым.
Проведем оценку адекватности регрессионной модели 
, выражающей зависимость среднего объема привлеченных средств банков от собственных средств, с помощью F критерия Фишера:
;
;
;
.
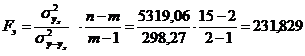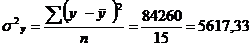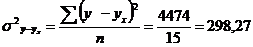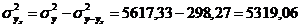Табличное значение Fт с уровнем значимости 0,05 и числом степеней свободы (2-1), (15-2) равно 4,68. (См. Приложение 7). Так как >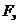 
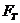, то уравнение регрессии можно признать адекватным.
При численности объектов анализа до 30 единиц (при малой выборе) возникает необходимость испытания параметров уравнения на их типичность (значимость). При этом осуществляется проверка, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатами действия случайных причин.
Для проверки значимости параметров уравнения регрессии используется t – критерий Стьюдента. Вычисляются фактические значения t критерия:
Для параметра 
:
;
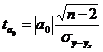для параметра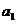 
:
,
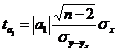где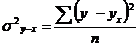 
- среднее квадратическое отклонение результативного признака от выравненных значений 
;
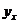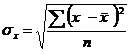- среднее квадратическое отклонение факторного признака хот общей средней 
.
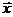Полученные фактические значения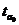 
и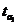 
сравниваются с критическим 
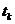, который получают по таблице Стьюдента с учетом принятого уровня значимости а (а=0,01 или а=0,05) и числа степеней свободы k=n-2.
Параметр признается значимым (типичным), если эмпирическое значение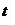 
больше критического табличного :
> < .
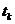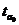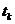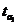Оценим значимость параметров уравнения регрессии с помощью t – критерия Стьюдента:
;
;
;
.
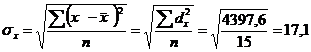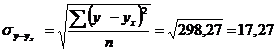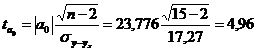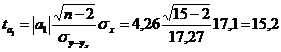Табличное значение t – критерия с уровнем значимости 0,05 и числом степеней свободы k=n-2=15-2=13 равно 2,161 (Приложение 6).
Сравним фактические значения 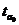и 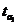с критическим ( 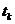=2,161), получаем:
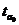= 4,96 > 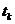= 2,161< 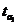=15,2.
Следовательно, вычисленные по уравнению регрессии параметры и 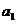признаются значимыми.
Измерение тесноты корреляционной связи.
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Теснота связи между двумя признаками может измеряться линейным коэффициентов корреляции (r), корреляционным отношением ( 
) и индексом корреляции (R).
Линейный коэффициент корреляции определяется по формулам:
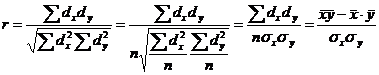
или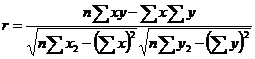 
.
Линейный коэффициент корреляции характеризует степень тесноты только при прямолинейной корреляционной зависимости. С коэффициентом регрессии 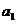связан таким соотношением: 
.
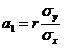Величина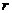 
принимает значения в интервале: 
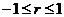. Отрицательные значения указывают на обратную связь, положительные – на прямую. При 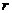=0 линейная связь отсутствует. Чем ближе 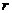по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при 
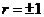, связь функциональная.
Квадрат линейного коэффициента корреляции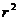 
называется линейным коэффициентом детерминации, показывает удельный вес влияния данного фактора в общей сумме всех факторов, определяющих уровень результативного признака.
Линейный коэффициент корреляции предложили в конце XIX века английские ученые Ф. Гальтон и К. Пирсон.
При наличии криволинейной корреляционной связи 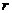недооценивает тесноту связи и в некоторых случаях может дать неверное представление о степени тесноты связи.
Теоретическое корреляционное отношение ( ) и индекс корреляции ( 
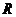) служат для измерения тесноты связи как при прямолинейной, так и при криволинейной корреляционной связи.
Теоретическое корреляционное отношение определяется по формулам:
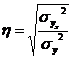или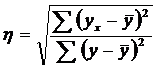 
.
Корреляционное отношение в квадрате 
показывает, какую часть всей вариации результативного признака составляет вариация, вызванная факторным признаком.
Для упрощения расчетов степени тесноты связи часто применяется индекс корреляции. Индекс корреляции определяется по следующим формулам:
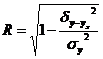или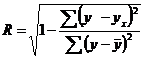 
.
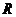Абсолютные размеры линейного коэффициента корреляции, корреляционного отношения, индекса корреляции колеблются от 0 до 1. Направление связи (знак перед и ) определяется непосредственно по исходным данным.
Для качественной оценки тесноты связи можно воспользоваться также шкалой Чеддока:
| Величина показателя тесноты связи | Характеристика тесноты |
| 0,1- 0,3 0,3 – 0,5 0,5 – 0,7 0,7 – 0,9 0,9 - 0,99 | Слабая Умеренная Заметная Высокая Весьма высокая |
Показател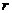и и при прямолинейной связи совпадают. Поэтому вычисленные по одним и тем же данным величины 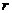и часто используют для того, чтобы судить о том, насколько для данного случая правильно предположение о наличии именно прямолинейной формы корреляционной связи. Английский статистик Блекман предложил следующий критерий: если разность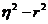 
не превышает 0,1, предположение о прямолинейной форме корреляционной связи можно считать оправданным.
При выборе вида уравнения можно воспользоваться еще критерием криволинейности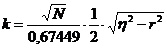 
, если k> 2,5, то предположение о данном виде криволинейной связи можно считать оправданным.
Используем данные табл. 7.7 и рассчитаем линейный коэффициент корреляции, теоретическое корреляционное отношение и индекс корреляции:
;
;
;
;
.
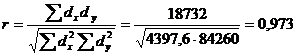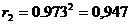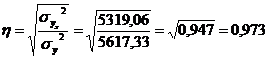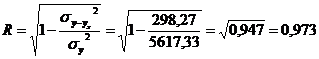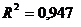Все показатели тесноты корреляционной связи показывают весьма высокую связь между объемами привлеченных и собственных средств.
Коэффициент детерминации 0,947 означает, что вариация привлеченных средств банков на 94,7% объясняется вариацией собственных средств и на 5,7% - прочими факторами.
Так как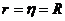 
, то можно седлать заключение, что гипотеза о линейной форме связи подтверждена.