Этап. Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

60Х1+70Х2+120Х3+130Х4 = Fmax – целевая функция прибыли.

{Х1+Х2+Х3+Х4 <= 16

{6Х1+5Х2+4Х3+Х4 <= 110 - ограничения модели

{4Х1+6Х2+10Х3+13Х4 <= 100

Х_j >=0 - граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Этап. Создание формы

а). Составление формы в виде:

	A	B	C	D	E	F	G	H
	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
	Значение
	Коэф. ЦФ					=СУММПРОИЗВ (В$2:Е$2;В3:Е3)	max
	Трудовые					=СУММПРОИЗВ (В$2:Е$2;В4:Е4)	<=
	Сырьевые					=СУММПРОИЗВ (В$2:Е$2;В5:Е5)	<=
	Финансы					=СУММПРОИЗВ (В$2:Е$2;В6:Е6)	<=

б). Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 - свободных членов из системы (2).

в). Ввод формул с помощью f_x - Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3, затем по значку Мастера функций fx на панели инструментов, в появившемся окне "Мастер функций, Шаг 1" выбрать категорию "Математические", далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне "Мастер функций Шаг 2" в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться Х1..Х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60Х1+70Х2+120Х3+ 130Х4

в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2, установив курсор перед нужным адресом B2и нажав функциональную клавишу F4, затем повторить эти действия для адреса E2. Формула примет следующий вид:

СУММПРОИЗВ($В$2:$Е$2;В3:Е3)

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3, содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

- в ячейке F4 - СУММПРОИЗВ($В$2:$Е$2;В4:Е4),

- в ячейке F5 - СУММПРОИЗВ($В$2:$Е$2;В5:Е5),

- в ячейке F6 - СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Этап. Заполнение окна Поиск решения

Выбрать в пункте меню Сервис команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3в форме (или ввести F3 с клавиатуры), поставить переключатель в положение "Максимальному значению" (см. Рис. 6.1). В поле "Изменяя ячейки" ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу "Добавить", в окне "Добавление ограничения» в поле "Ссылка на ячейку" ввести F4, выбрать через "стрелка вниз" знак "<=", в поле справа ввести Н4(Рис. 6.2).

Аналогично через "Добавить" ввести F5<=H5, F6<=H6 для системы ограничений (2), а также B2>=0, C2>=0, D2>=0 и Е2>=0.

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо "Добавить" нажать клавишу ОК, появится окно "Поиск решения".

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Этап. Параметры поиска.

В окне "Поиск решения" нажать клавишу "Параметры", выбрать по умолчанию Максимальное время - 100 с.(может быть до 2^15=32767 c.> 4 час.), число итераций- 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке "Линейная модель", нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (Рис. 6.3).

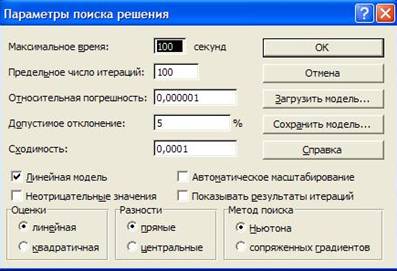
Рисунок 6.3 Диалоговое окно Параметры поиска решения

Результаты поиска решения с таблицей результатов:

	A	B	C	D	E	F	G	H
	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
	Значение
	Коэф. ЦФ						max
	Трудовые						<=
	Сырьевые						<=
	Финансы						<=

Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0)

при минимальном использовании ресурсов

-Трудовые - 16 (У1)

-Сырьевые - 84 (У2)

-Финансы - 100 (У3)

даёт максимум прибыли F в 1320 руб.

Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых (У1) и финансовых (У3) ресурсов приведёт к изменению прибыли F, а изменение сырьевых ресурсов (У2) - нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными У1, У2 и У3 сопряжённой задачи линейного программирования. В данном случае У1=У3=0, а У2=26 ед. Таким образом, ресурс У2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.