Семестр3элементытеориимножеств

СЕМЕСТР3ЭЛЕМЕНТЫТЕОРИИМНОЖЕСТВ

Понятиемножестваилисовокупностипринадлежиткчислупростейшихматематическихпонятий.Ононеимеетточногоопределения.Любоемножествозадаетсясвоимиэлементами.Примерамиявляютсямножествокнигвбиблиотекеилимножествостудентов,присутствующихназанятии.Обычномножествообозначаютзаглавнымилатинскимибуквами(A),аегоэлементыстрочнымилатинскимибуквами(a).То,чтоэлементпринадлежитмножеству,обозначаюттак:aÎA.ЕслиaнепринадлежитA,тоэтотфактобозначаюттак:aÏA.ЕсливсеэлементымножестваAпринадлежатмножествуB,тоA–подмножествомножестваB(AÌ B).

Чтобызадатьмножество,следуетилиперечислитьегоэлементы,или

указатьхарактеристическоесвойствоегоэлементов,тоестьтакоесвойство,которымобладаютвсеэлементымножестваитолькоони.Мыужезнакомысоследующимипримерамиподмножеств вещественныхчисел.

Примеры.

1. Множествонатуральныхчисел:N={1,2,3,…,n,n+1,…}.Иззаписи

следует,чтовсенатуральныечисла,начинаясдвойки,получаютсяприбавлениемединицы к предыдущемучислу.

2. Множествоцелыхчисел:Z={0, 1,–1, 2,–2,…,n, –n,…}.

3. Множество рациональных чисел: Q={p|pÎZ,qÎ N}.

q

Вертикальнаячертаозначает,чтозанейуказываетсяхарактеристическоесвойствоэлементовмножества.

4. Рассмотрим множество C комплексных чисел:

C= {z= x+ iy|x,yÎR},гдеi– число,удовлетворяющеесвойству:

i2= -1.

Очевидно,чтотакогочисланесуществуетнадействительнойпрямой.Поэтомудляинтерпретациикомплексныхчиселиспользуютточкиплоскости,накоторойвведеныдвекоординатныеоси.Однасовпадаетсдействительнойпрямой,инанеепроецируютдействительнуючастькомплексногочисла(x). Другая–мнимаяось–перпендикулярнадействительнойоси,инанеепроецируюткоэффициентприi(мнимуючасть числа).

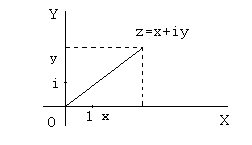
Множество действительных чисел R является подмножеством

множестваC(вслучае,когда

y= 0).Необходимостьвкомплексныхчислах

возникаетужетогда,когдамырешаемквадратноеуравнениеисталкиваемсясо случаемотрицательногодискриминанта.Например,решаяуравнение

t2- 2t+ 5= 0

с отрицательным дискриминантом, мы получим корни

t1,2=1± -4

или

t1,2=1± 2i. В комплексной плоскостидва этих

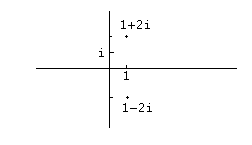комплексных числа выглядят так:

Очевидно,чтоNÌ ZÌ QÌ RÌ C.

Двамножестваравнытогда итолькотогда,когдасостоятиз однихитех

жеэлементов.ПоэтомуA= B

означает,чтоAÌ BиодновременноBÌ A.

Врамкахрассматриваемойматематическойтеориивводятдваисключительныхмножества:пустоемножество(Æ ),несодержащееэлементов,иуниверсальноемножествоили«универсум»(U),содержащеевсе элементыданнойтеории.

Декартовопроизведениемножеств

A\B= AÇ Bc.

ПустьAи B– подмножествамножестваRвещественныхчисел.

ДекартовымпроизведениемэтихмножествA´ B

назовемтакоемножество

точекскоординатами(x,y)наплоскости

R2, что xÎ A

иодновременно

yÎB.Например,еслиAпредставляетотрезок[0,2],аB–отрезок[-1,6],то

A´ B

– этопрямоугольникс соответствующимисторонами.Аналогично

вводитсядекартовопроизведениетрехиболее множеств.

ЭЛЕМЕНТЫКОМБИНАТОРИКИ

РЯДЫ

Числовыеряды

Понятиепределапоследовательностидаетвозможностьввестипонятие

¥

числовогоряда–бесконечнойсуммывида

åak,где

k=1

ak–общийчленряда.

Напервыйвзглядбесконечноесуммированиеневозможноужехотябывсилуконечностижизнилюбого,ктозанимаетсясуммированием.Выходизположенияследующий:бесконечнаясуммапонимаетсякак предел

n

последовательности

sn–конечныхn- ныхчастныхсумм

¥

sn= åak.Таким

k=1

образом,суммойряда

åakбудем называтьчисло

k=1

å k

n

s= lim a.

n®¥ k=1

Рядназываетсясходящимся,еслидлянегосуществуетконечнаясумма.Рядназываетсярасходящимся,еслисоответствующийпределчастныхсуммне существует или бесконечен.

Пример 1. Сосчитаем сумму ряда

¥

åqk, |q|<1. Имеем согласно

k=1

формулесуммыгеометрическойпрогрессии

sn=

n

å

k=1

qk= q× qn-1.Поскольку

q-1

qn® 0

приn®¥,получим

¥

åqk=

k=1

q .

1- q

Заметим, чтопри|q|³1соответствующийрядрасходится.

¥

Пример 2. Сосчитаемсуммуряда å 1

. Имеем

sn= 1 + 1

+...+ 1

k=1k(k+1)

= 2-1+ 3- 2+...+n+1- n=

1×2 2×3

n(n+1) 1×2 2×3

n(n+1)

=1- 1+ 1- 1+...+ 1- 1

=1- 1 ,

¥

2 2 3

n n+1

n+1

следовательно,å 1

=1.

k=1k(k+1)

Необходимым признаком сходимостичислового ряда является

¥

n

условие:lima= 0.Доказываетсяэтолегко:пустьряд

n®¥

åakk=1

сходится,тоесть

n

существует lims= s. При n®¥справедливо:

n®¥

n-1® ¥ . Следовательно,

n-1

lims = s. Поскольку

n®¥

sn- sn-1= an, то из1-гои 2-госвойствпределов

последовательностейимеем:

liman= lim(sn- sn-1)= 0, что и требовалось

доказать.

n®¥

n®¥

å

Заметим,чтонеобходимоеусловиесходимостинеявляетсядостаточным.Тоесть,стремлениекнулюобщегочленаряданеобеспечиваетегосходимость.

Контрпример. Покажем,чторяд

¥ 1, называемыйгармоническим

k=1k

рядом,расходится.Дляэтогорассмотримпоследовательностьчастныхсумм

s2n,то естьчастныесуммы

s2,s4,s8,.....Присуммированиичленовконечной

суммы

s2n

сгруппируемрядомстоящиечленысуммы,начинаяот

до

2l+1

2l+1,привсехl=1,...,n-1:

sn=1+ 1+ (1+ 1)+ (1+...+ 1)+...+ ( 1

+...+

1)>

2 2 3 4 5 8

2n-1+1 2n

>1+ 1+ 2× 1+ 4× 1+...+ 2n-1× 1

=1+ n× 1.

2 4 8 2n 2

Таким образом,

lims2

=¥ , и значит, предел последовательности

n®¥ n

частныхсуммне можетбыть конечным.

Свойствачисловых рядов

Следующиесвойствасходящихсярядовочевиднымобразомследуютизсвойствпределовпоследовательностей.

¥ ¥ ¥ ¥

1. Пустьряды

¥

åak и

k=1

åbkk=1

сходятся, причем

åak= s,

k=1

åbk= s .

k=1

Тогдаряд

å(a × ak + b ×bk)

k=1

также сходится, причем

¥

å(a × ak + b ×bk)= a × s+ b ×s .

k=1

2. Ряды

¥

åakk=1

¥

и åak+ Nk=1

сходятсяилирасходятсяодновременно,

причем

¥ ¥

åak+N= åak- sN.

k=1

k=1

Знакопеременные ряды

Длязнакопеременныхрядовприведенныепризнакисходимоститакжеможноприменять,нодляисследованияабсолютнойсходимости.Делов

том,чтоеслиряд

¥

¥

å|ck|

k=1

сходится,тосходитсяиряд

¥

åck,причемвэтом

k=1

случаеряд

åckназываетсяабсолютносходящимся.Такимобразом,если

k=1

имеетсязнакопеременныйряд

¥

åck,имеетсмыслпроверитьвозможность

k=1

применениякакого-либопризнакасходимостикряду

¥

¥

å|ck|,иеслиусловия

k=1

сходимостивыполняются, исходныйряд

åckсходитсяабсолютно.

k=1

Пример. Ряд

¥

å

k=1

(-1)k

ka

сходитсяабсолютноприa >1.

ПризнакЛейбницасходимостизнакочередующегосяряда. Пусть

членыположительнойпоследовательности

¥

ak,монотонноубывая,стремятся

k-1

кнулюприk®¥ .Тогдаряд

å

k=1

(-1) ak

сходится.

Доказательство.Рассмотримпоследовательностьчетныхчастныхсумм

s2n= a1- a2+ a3-......+ a2n-1- a2n= (a1- a2)+ (a3- a4)+...+ (a2n-1- a2n)> 0.

Очевидно,чтосростомnзначения

s2n

возрастают.Теперьзапишемэтуже

частную сумму в ином виде:

s2n= a1-(a2- a3)-......- (a2n-2- a2n-1)- a2n.

Очевидно,что

s2n< a1.Такимобразом,мыимееммонотонновозрастающую

ограниченную сверху последовательность

s2n. По одному из свойств

последовательностей существует

lims = s. Итак, последовательность

2n

n®¥

частныхсуммс четныминомерамиимеет предел.Чтоже с нечетнымичастнымисуммами?

Так как

s2n+1= s2n+ a2n+1 и

lima2n+1= 0, то существует

n®¥

lims2n+1= lims2n+ lima2n+1= s.Следовательно,существуетlimsn= s.

n®¥

n®¥

n®¥

n®¥

Пример. Ряд

¥

å

k=1

(-1)k

ka

сходитсяпопризнакуЛейбницаприлюбом

a > 0.

В предыдущем примере, опираясь на интегральный признак, мы

показали,чтоэтотрядпри

a >1

сходитсяабсолютно.При 0<a £1

рядне

может абсолютносходиться.Ноон сходитсяпопризнакуЛейбница.

Ряд,сходящийся, нонесходящийсяабсолютно,называетсяусловносходящимся.

Функциональныеряды

{ n }

Пусть f(x) ,

nÎN

xÎM,

–последовательностьфункций,заданныхна

одномитомжемножестве,причемприкаждомзначении

¥

x0ÎM

числовой

ряд

¥

å fk(x0)

k=1

сходится. Тогдамы можемрассматриватьфункциональныйряд

å fk(x)

k=1

намножествеM иисследоватьсвойствафункции

s(x)–суммы

ряда –на томже множествеM.

В связи с вопросамисходимостифункциональныхрядовотметимследующийиз теоремысравнениямажорантныйпризнаксходимости

функциональногоряда:если

$an> 0такоечто

¥

"xÎM,

"nÎN(|fn(x)|£ an)

ирядсположительнымичленами

¥

åakk=1

сходится,тофункциональныйряд

å fk(x)

k=1

абсолютносходится намножествеM.

Степенные ряды

Простейшимпримеромфункциональногорядаявляетсястепеннойряд–

¥

рядвида

åck

k=0

(x- a)k. Числа

ck,k= 0,1,..., называются коэффициентами

степенногоряда.Посколькупростойзаменойпеременнойx= x- a

¥

исходный

k

степеннойрядпревращаетсявряд

å

k=0

ckx,мыбудемрассматриватьтолько

степенныерядывида

¥

å

k=0

k

ckx.Очевидно,чтотакойрядобязательносходится

вточкедает

x= 0.Ответомнавопрособобластисходимостистепенногоряда

ТеоремаАбеля.Пустьряд

¥

å

k=0

k

ckx

сходитсявточке

x= x1,тогдаон

сходится,причемабсолютно, при"x,|x|<|x1|.

¥

k

Пустьряд

"x,|x|>|x2|.

å

k=0

ckx

расходитсявточке

¥

x= x2

,тогдаонрасходитсяпри

k

Доказательство.Так какряд

åckx1

сходится,тообщийчленэтогоряда

k=0

стремитсяк нулю, изначит,ограничен,то есть,

k

$M> 0

k 1

тчо|cxk|£ M.

k

Пусть

|x|<|x1|

тогда

|cxk|£ Mx

k

x

.Таккакряд

¥ x

å

Mx

сходится,

то потеоремесравненияабсолютносходитсяряд

¥

k

åckx1

k=1 1

.

Таккак

¥

k

åckx2

k=0

расходится,то

¥

å

k=0

k

ckx

k=0

не может сходитьсянипри

какихзначениях

x, |x|>|x2|,таккаквпротивномслучаеонбысходился,в

соответствии с доказаннойчастьютеоремы, ипри

x= x2.

ИзтеоремыАбеляследует,в частности,чтообластьсходимости

¥

k

степенногоряда

å

k=0

ckx

представляетсобойнекоторыйинтервал(-R,R),а

областьрасходимости–внешностьэтогоинтервала.Чтокасаетсядвухточекx= ±R,являющихсяграницамиэтогоинтервала,тосходимостьилирасходимостьрядавэтихточкахследуетпроверятьдлякаждойфункциииндивидуально.

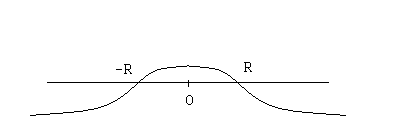
Число Rназываетсярадиусомсходимостистепенногоряда.Интервал

(-R,R)

называетсяинтерваломсходимостистепенногоряда.

Способыопределениярадиуса сходимостистепенногоряда

1. В соответствии с признаком Даламбера если

|c xn+1| |c

||x| ¥

|c ||x|

lim

n+1

= lim

n+1

<1,то

å|cxk|

сходится,если

lim

n+1

>1,

n®¥

|cnxn+1|

¥

å

n®¥

k

|cn|

kk=0

n®¥

|cn|

то ряд

k=0

|cxk|

расходится. Следовательно, при |x|= R

имеем:

lim|cn+1|R=1

или

R= lim

|cn|.

n®¥

|cn|

n®¥ |cn+1|

2. АналогичноиспользуяпризнакКоши, получим

R= 1 .

n

limn|c |

n®¥

¥ xn

Пример1.Найтиобластьсходимостистепенногоряда

å p.Найдем

n

n=1

радиуссходимости.Здесь

c= 1

. Следовательно,

R= lim(n+1)p

=1.

n np

Проверим сходимость в точке

n®¥

x=1. Имеем ряд

np

¥

å p, который

сходится, если

p>1ирасходится,если

p£1.

n=1n

Проверимсходимостьв точке

x= -1.Имеемряд

¥

å

n=1

(-1)n, который

np

сходится, если

p> 0

и расходится, если

p£ 0.

Замечание.Внутри интервала сходимости ряд можно почленноинтегрироватьидифференцироватьлюбоечислораз.Этозначит,чтоесли

¥ b ¥ b

k

k

åckx= s(x),|x|< R,то1)

ò s(x)dx= å

ckò xdx,|a|,|b|< R,

k=0

2)(s(x))(m)=

¥

å ck

k=m

a

(xk)(m),|x|< R.

k=0 a

Примерыразложенияфункцийв рядыТейлора

Пример1. Рассмотримфункцию

ex. В соответствиис формулой

x x x2 x3 xn

Тейлора-Маклоренаe

|rn(x)|£ e

=1+1!+ 2!+ 3!+×××+ n!+ rn(x),

× |x|n+1.

(n+1)!

где max{x,0}

Сосчитаемрадиуссходимостистепенногоряда:

R= lim(n+1)!= lim(n+1)= ¥ .

n®¥ n!

n®¥

Такимобразом, этотрядсходитсявовсехточкахвещественнойоси.Для

¥ xk

того,чтобывыяснить,будетлисходитьсяряд

å кфункции

k!

k=0

| |n+1

ex,заметим,

чтоприлюбомзначении

xÎR

имеем |rn(x)|£ e|x|×

x ® 0 (n+1)!

при n®¥.

¥

å

Следовательно,ex= xk

k

привсех

xÎR.

k=0 !

Пример 2. Рассмотрим функциюформулойТейлора-Маклорена

f(x) = sinx. В соответствии с

1 1 1

(-1)n+1

sinx= x-

x3+

x5+×××+

( )

x2n-1+ r(x),

1! 3! 5! 2n-1! n

где

|r(x)|£ |x|2n+1.Тоесть,

R= lim

(2n+1)!= ¥ и

rn(x)® 0

при n®¥.

n

(2n+1)!

¥

(-1)n+1

n®¥ (2n-1)!

Следовательно,

sinx= å

( )

n=12n-1!

x2n-1

привсех

xÎR.

Пример 3. Рассмотрим функциюформулойТейлора-Маклорена

f(x) = cosx.

В соответствии с

111

(-1)n

cosx=1-

x2+

x4 -

x6+×××+

( )

x2n+ r(x),

2! 4! 6! 2n

|x|2(n+1)

! n

(2n+2)!

где

|rn(x)|£ (2n+ 2)!. Тоесть,

¥ (

R= lim

n®¥

-1)n

(2n)!

= ¥ и

rn(x)® 0

при

n®¥.Следовательно,

cosx= å

( )

n=02n!

x2n

при всех

xÎR.

Пример 4. Рассмотрим функцию

f(x) = (1+ x)a ,

a ÏN. В

соответствиисформулойТейлора-Маклоренаприa ÏN

+ = +a

+ a a-

+ + a a- a- a- + + .

(1 x)a 1 x

( 1)x2

2!

...

( 1)( 2)...(

n!

n 1)xn

rn(x)

Найдемрадиуссходимостиэтогостепенногоряда:

R= lim

n+1

=1.

n®¥ a - n

Дляоценкиостаточногочленаприn,большихилиравныхцелойчастиa ,

формаЛагранжаостаточногочленагодитсятолькодля

x> 0.Вэтомслучае

имеем оценку:

|rn(x)|£ |a(a-1)(a- 2)...(a- n)|x|(n+1). Очевидно, что при

(n+1)!

0< x<1

имеем

rn(x)® 0

при n®¥.Для отрицательныхзначений x

применяетсядругаяформа остаточногочлена. В результатедля |x|<1

справедливопредставление

(1+ x)a =1+

¥

å

n=1

a(a -1)(a - 2)...(a - n+1)xn.

n!

В случае,когда

a = m

– натуральноечисло,производныефункции

(1+ x)m

порядка выше, чем m, обращаются в 0. Следовательно,

коэффициентырядапристепеняхвышеm– нулевые, изначит,отряда

останетсятолькоконечнаясумма,содержащая

это имеетвид

m+1слагаемое.Разложение

(1 x)m 1

mm(m-1)(m- 2)...(m- n+1)xn 1

m

Cnxn

+ = + å

n=1

= + å m ,

n=1

n!

а полученнаяформуланосит название«биномНьютона».

ПримерыприложенийрядовТейлора.

Представленныевпредыдущемпунктеканоническиеразложениямогут

служитьосновойдляполученияновыхразложений.Так,положив

a = -1в

последнем разложении, мы получим формулы суммы бесконечнойгеометрической прогрессии со знаменателем (-q):

1- q+ q2+...+ (-q)n+...=

1+ q

.Замениввэтойформулеqна(-q),получим:

1+ q+ q2+...+ qn+...=

1 .

1- q

Заменим впоследней формулеqна

-t2,мыполучимразложение

1+ t2

¥

= å

n=0

(-t2)n,

|t|<1. Последний ряд имеет радиус сходимости,

равный1.Вспомним,чтовнутриинтерваласходимостирядыможноинтегрироватьпочленноипроинтегрируемобечастипоследнегоравенствапоtот0до

x

¥ 2n+1

n=0

n

x, |x|<1,тогдаполучимразложение:

arctgx= å(-1) 2n+1.

Еще легче получить разложение

ln(1+ x)= å (-1)

n+1xn

,

если

¥

n=1 n

проинтегрировать почленно ряд

1-t+ t2+...+ (-t)n+...=

1+ t

внутри

интерваласходимости,тоесть при|t|<1.

Разложенияфункций

ex, sinx

и cosxврядыТейлора,справедливые

длявсехвещественныхx,оказываютсятакимижеивслучае,когда x–

комплексноечисло.Пустьx= i×t,гдеi–мнимаяединица,тоесть,

i2= -1,а

t– вещественноечисло.(Заметим,чтоТейлора:

i3= -i,

i4=1).Разложим

ei×t

вряд

2 3 4 5 6 7 2 4 6

ei×t= + i×t- t

- it+ t

+ it- t

- it

+ = - t+ t

– t+ +

1

t3 t5

2! 3! 4! 5! 6! 7!

t7

..... (1

2! 4! 6!

...)

+i(t- 3!+ 5!- 7!+....)= cost

+ i×sint.

Вотэтаформула,выражающаясвязьмежду

ex, sinx

иcosxвслучае

комплексныхпеременных, и называетсяформулой Эйлера.

РядыТейлораслужатдляприближениямногихфункций.Деловтом,чтоарифметическиеоперации,которыепроводятсяточно–этооперацииумноженияначисло(аследовательно,ивозведениевцелуюположительнуюстепень)и сложение.Поэтомувычислениезначениймногих известных

функций,например,

ex,sinx,cosx,lnx, сводится к вычислениюзначений

близкихкэтимфункцияммногочленов–частныхсуммсоответствующихрядовТейлора.Этисуммызаложенывпрограммувычисленийнашихкалькуляторов.

ЧастныесуммырядаТейлора

n

å

k=0

f(k)(0)xk

k!

дляпроизвольнойфункции

f(x)можнополучатьс помощьюпрограммыMAXIMA.Длятого,чтобы

получить

n (k)

f

å

(a)(x- a)k

дляконкретнойфункции

f(x),следуетнабрать

k=0 k!

taylor(f(x),x,a,n)и нажать Shift+Enter.

Пример. ДляполучениясуммыТейлора7-йстепенипостепеням(x-1)

для функции lnx

x

следует набрать taylor(log(x)/x,x,1,7).Мы получим

x-1-3(x-1)2/2+11(x-1)3/6-25(x-1)4/12+137(x-1)5/60-49(x-1)6/20+

+363(x-1)7/140+.

Сравнимполученныймногочлен(красныйграфик) сисходнойфункцией

lnx

x (синийграфик)на одномрисунке.Для этоговведемload(draw);

draw2d(color=blue, explicit(log(x)/x,x,0.2,2), color=red,

explicit(taylor(log(x)/x,x,1,7),x,0.2,2))

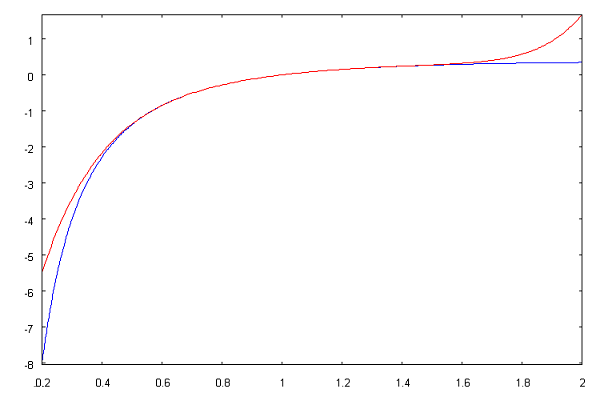
Мы видим,что красныйи синийграфикисливаютсяв окрестности

точки

x=1иудаляютсядруготдругаприудаленииаргументаотзначения1.

Этосвидетельствуетотом,чточастныесуммырядовТейлораприближают

функцию тольков окрестноститочки

x=1.

ТригонометрическиерядыФурье

Вразличныхотрасляхнауки,втомчисле,вфизикеприходитсяиметьдело с периодическимиявлениями.Простейшийпример– электрические

колебания. Периодической называется функция

f(x), для которой

существует такая величина,называемая периодом, что

f(x)=

f(x+T).

Простейшими T- периодическими функциями являются

тригонометрическиефункциивида

sin2pkx,cos2pkx,где k–целоечисло,

T T

называемыегармониками.Представлениепериодическойфункцииввиде

суммыгармоникназываетсягармоническиманализом.Вслучае,когдатакая

суммабесконечна,мыполучаемтригонометрическийряд, называемыйрядомФурье.

Итак, пусть непрерывная T- периодическая функция

f(x)

представлена в виде тригонометрического ряда:

å

f(x)= a0+ ¥ a

cos2pkx+ b

sin2pkx. Возникает вопрос: как найти

2 k=1k

T k T

коэффициенты

a0,ak,bk,

kÎN?

Воспользуемся тем,что гармоникиобладают следующимсвойством:

T/2

ò

-T/2

T/2

ò

-T/2

T/2

cos

sin

2p kxT

2p kxT

dx= 0,

dx= 0,

ò

-T/2

T/2

ò

-T/2

T/2

ò

-T/2

T/2

ò

cos2plxsin2pmxdx= 0,

T T

cos2plxcos2pmxdx= 0,

T T

sin2plxsin2pmxdx= 0,

T T

cos22plxdx= 2,

"l,mÎ N,

"l,mÎN,l¹ m,

"l,mÎ N,l¹ m,

-T/2

T/2

ò

-T/2

T T

sin22plxdx= 2.

T T

Теперьдлятого,чтобы,например,найтиравенства

am умножимобечасти

å

f(x)= a0+ ¥ a

cos2pkx+ b

sin2p kx

на cos2pmx

ипроинтегрируем

2 k=1k

T k T T

наотрезке[-T/2,T/2].Сучетомсвойствгармониквправойчастиравенства

останется только слагаемое

a 2, а в левой части – выражение

m

T

T/2

ò

-T/2

f(x)cos

2p mxT

dx.Отсюдамыполучим

am.

Умножаянаsin2pmx

T

иинтегрируя,получимbm.

Адлятого,чтобыполучить

a0,нужнопростопроинтегрироватьобе

части равенства

f(x)= a0+ ¥ a

cos2pkx+ b

sin2p kx

на отрезке

å

[-T/2,T/2].

2 k=1k

T k T

Таким образом, непрерывная периодическая функцияпредставима в видеследующеготригонометрическогорядаФурье:

f(x)

å

f(x)= a0+ ¥ a

cos2pkx+ b

sin2pkx, где

2T/2

k=1

k T k T

2p kx

ak= T

ò

-T/2

f(x)cos T

dx,

k= 0,1,2,....,

b = 2

k T

T/2

ò

-T/2

f(x)sin

2p kxT

dx,

k=1,2,....

Вслучае,когдапериодическаяфункцияимеетточкиразрыва,еетакжеможнораскладыватьврядФурье,норавенствофункцииисуммырядабудеттольковточкахнепрерывностифункции.ВточкахразрыварядФурьебудетсходитьсякполусуммезначенийфункциислеваисправаотточкиразрыва:

¥

a0+ åa

cos2pkx0+ b

sin2pkx0= 1(f(x

- 0)+ f(x

+ 0)).

2 k=1k

T k T 2 0 0

ВозможноразложениефункцииврядФурьеспомощьюMAXIMы.Мы

получимвсе коэффициентырядаФурье дляфункции

f(x), заданнойна

отрезке[-T,T]

иT-периодическипродолженнойнавсювещественнуюось,

если введем load(fourie); fourier(f(x),x,t) и нажмемShift+Enter.

Пример.Получим коэффициенты ряда Фурье для функции

f(x)= ex,-p £ x< p . Для этого введемload(fourie);fourier(%e^x,x,%pi),

нажмем Shift+Enterи получим

a= (ep

-e-p

)/p ,

an= (nsinp n/(ep n2+ ep )+ ep nsinp n/(n2+1)-

-cosp n/(ep n2+ ep )+ ep cosp n/(n2+1))/p ,

bn= (sinp n/(ep n2+ ep )+ ep p sinp n/(n2+1)-

-ncosp n/(epn2+ ep )+ epncosp n/(n2+1))/p.

Мы видим,что коэффициентысодержатвыражения sinp n= 0и

cosp n= (-1)n.Поэтомупреобразуемкоэффициенты:

a0=

ep - e-p ,

p

n

a= (-1) ( 1

ep ),

-

n p ep (n2+1) (n2+1)

n

b= (-1)n(- 1

ep ).

+

n p ep (n2+1) (n2+1)

Длятого,чтобынетольковычислитькоэффициентырядаФурье,нои

получитьразложениефункции

f(x), заданнойна отрезке[-T,T]

и T-

периодическипродолженной на всювещественную ось врядФурье, следуетввестиload(fourie);totalfourier(f(x),x,T)и нажать Shift+Enter.

Пример.ДляразложенияврядФурьефункцииизпредыдущегопримеравведемload(fourie);totalfourier(%e^x,x,%pi).Приэтомполучимразложение

¥

e-p (ep -1)(ep +1)å

– n=1

n(-1)nsinnx

n2+1

¥

e-p (ep -1)(ep +1)å

+ n=1

(-1)ncosnx

n2+1 +

p p

+ e-p (ep -1)(ep +1)

2p .

Следует отметить, что частные суммы ряда Фурье приближаютисходнуюфункциюне в конкретныхточках,а «всреднемпо отрезку».

Сравнимзаданнуюфункцию

y= ex,-p £ x£ p ,и9-ючастнуюсуммуряда

Фурье на одном графике. Для этого сначала введем функцию

g(x),

совпадающуюс9-йчастнойсуммой,азатемнарисуемфункциюex

(черным

цветом)ифункцию

[-p ,p ]:

g(x)

(краснымцветом)наодномграфикенадотрезком

g(x):=-(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum((n*(-

1)^n*sin(n*x))/(n^2+1),n,1,9))/%pi+(%e^(-%pi)*(%e^%pi-

1)*(%e^%pi+1)*sum(((-1)^n*cos(n*x))/(n^2+1),n,1,9))/%pi+

(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1))/(2*%pi);

load(draw); draw2d(explicit(%e^x,x,-%pi,%pi), color=red,explicit(g(x),x,-%pi,%pi)).

В результате получимкартину

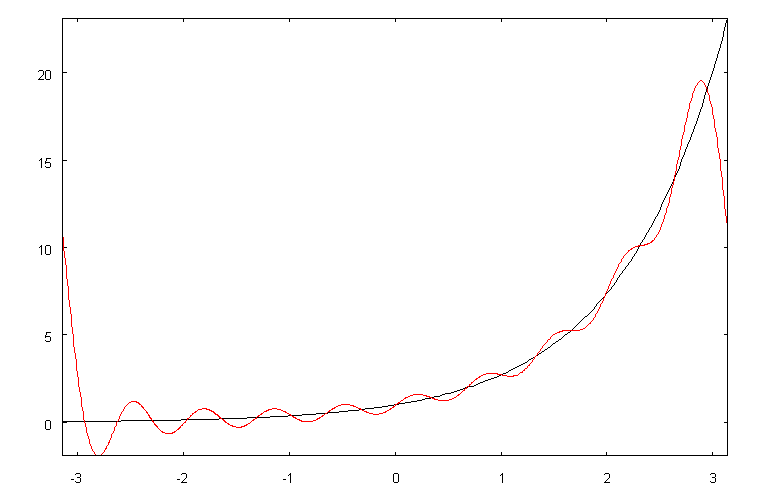
Здесь видно, что в конечных точках отрезка, где функция

y= ex,-p £ x£ p , припериодическомпродолжениис отрезка [-p ,p ] в

другиеточкивещественнойоситерпитразрыв,графикчастнойсуммырядаФурье(краснаялиния)значительноотличаетсяотграфикаэкспоненциальнойфункции.Еслибратьчастнуюсуммусбольшимколичествомчленов,тографикчастнойсуммыбудеттеснееприближатьсякисходнойфункцииво

внутреннихточкахинтервала (-p ,p ),новблизиточекx= ±p

поведение

будет тем же из-за разрыва исходной функции при периодическомпродолжении.

ДИФФЕРЕНЦИАЛЬНЫЕУРАВНЕНИЯ

Дифференциальным уравнением называется соотношение вида

F(x,y(x),y¢,y¢,...,y(n))= 0. Решить дифференциальное уравнение – это

значит,определитьфункцию

y(x),удовлетворяющееэтомусоотношению,

возможно, в неявном или параметрическомвиде.

Простейшеедифференциальноеуравнениевида

y¢(x)=

f(x)

мы уже

решали, так как находили

y(x)= ò f(x)dx. Мы знаем, что интеграл

определяетсясточностьюдопроизвольногопостоянногослагаемого.Тоесть

решение простейшего дифференциального уравнения содержит

произвольнуюпостоянную.Решенияболеесложныхдифференциальныхуравненийтакженаходятсясточностьюдопроизвольныхпостоянных.Любуюфункцию,удовлетворяющуюдифференциальномууравнению,мыбудемназыватьчастнымрешениемэтогоуравнения,совокупностьчастныхрешенийназовемобщимрешениемдифференциальногоуравнения.

Порядокдифференциального уравнения определяетсянаивысшимпорядком входящих в него производных. Поэтому дифференциальное

уравнениевида

F(x,y(x),y¢,y¢,...,y(n))= 0

считаетсядифференциальным

уравнениемn-гопорядка.

Также,какнелюбаяфункцияможетбытьпроинтегрирована,ипредставленаввидеэлементарныхфункций,такинелюбоедифференциальноеуравнениеимеетрешение,выражающеесячерезэлементарныефункции.Классдифференциальныхуравнений,

интегрируемыхв квадратурах,узок.Мы изучимнесколькоклассов

дифференциальныхуравнений,интегрируемыхвквадратурах,атакжерассмотримнекоторыеприближенныеметодырешениядифференциальныхуравнений.Крометого,мырассмотримнекоторыезадачи,связанныесприменениемдифференциальныхуравнений.

УравнениеБернулли

К решению линейного уравнения сводится решение уравнения

Бернулли

y¢ = a(x)y+b(x)yn,где

n¹1.Действительно,еслиразделитьобе

части уравн<