Математического программирования

Множество 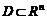называется ограниченным множеством, если расстояние 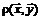между любыми двумя его точками 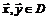меньше некоторого числа :

.

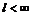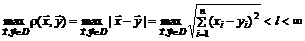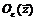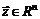Эпсилон-окрестностью точки называется множество точек, отстоящих от точки 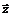на расстоянии меньшем, чем :

.

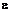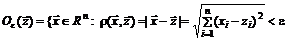Точка 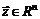называется предельной точкой множества 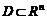, если существует последовательность принадлежащих 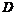точек 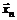, сходящаяся к 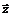, то есть если выполняется условие

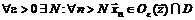
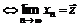. (1.10)

Множество 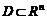называется замкнутым множеством, если оно содержит все свои предельные точки.

Множество 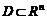называется компактным множеством, если оно ограничено и замкнуто.

Точка 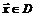называется внутренней точкой множества 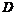, если существует 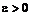такое, что 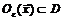. В противном случае точка 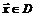называется граничной точкой множества .

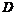Точка 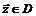называется точкой условного локального максимума (локального минимума) функции в области 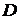, если существует окрестность 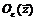такая, что для любой точки 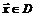из этой окрестности значение не больше (не меньше), чем :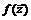

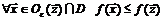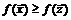( для минимума). (1.11)

Точка 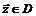называется точкой условного глобального максимума (глобального минимума) функции в области 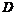, если значение 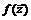не меньше (не больше), чем для любого :

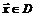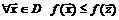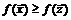( для минимума).

Говорят, что функция имеет в точке 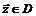условный локальный (глобальный) экстремум на множестве 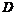, если точка 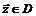является точкой локального (глобального) максимума или минимума.

Говорят, что функция имеет в точке 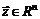локальный (глобальный) безусловный экстремум, если точка 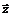является точкой локального (глобального) максимума или минимума на всем пространстве .

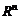Говорят, что функция дифференцируема в точке 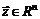, если в этой точке существуют все ее частные производные первого порядка

.

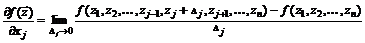Говорят, что функция непрерывно дифференцируема в точке 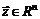, если все ее частные производные первого порядка непрерывны в этой точке.

Точка 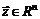, в которой равны нулю все частные производные первого порядка функции , называется стационарной точкой этой функции.

Точка 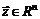называется седловой точкой (седлом) функции , если она является стационарной точкой, но не является точкой безусловного экстремума.

Говорят, что функция дважды дифференцируема в точке 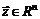, если в этой точке существуют все ее частные производные второго порядка

.

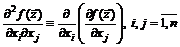Замечание 1.1. Значение частной производной второго порядка не зависит от порядка дифференцирования по переменным, то есть

.

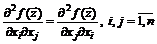Квадратная матрица 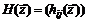, элементы которой определяются значениями частных производных второго порядка функции в точке 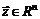, то есть

,

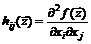называется матрицей Гессе функции в точке .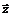

Выражени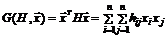е , где 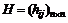– квадратная матрица, 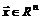, называется квадратичной формой матрицы .

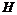Квадратнаяматрица 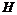называется положительно (неотрицательно) определенной, если справедливо

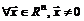
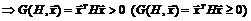. (1.12)

Квадратнаяматрица 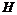называется отрицательно (неположительно) определенной, если справедливо

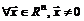
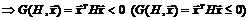. (1.13)

Квадратнаяматрица 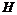называется неопределенной матрицей, если она не является ни положительно, ни отрицательно определенной.

Установить тип определенности матрицы Гессе в стационарной точке позволяет следующая теорема.

Теорема об условиях определенности матрицы (критерий Сильвестра).Справедливы следующие утверждения:

1) квадратная матрица положительно определена тогда и только тогда, когда значения всех ее главных миноров положительны.

2) квадратная матрица отрицательно определена тогда и только тогда, когда знак ее k-го главного минора определяется знаком .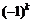

Пример 1.1. Матрицы 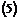, 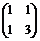определены положительно; матрицы 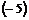, 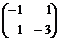определены отрицательно.

Функция 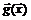называется m-мерной вектор-функцией, если она представляет собой m-мерный вектор, компоненты которого суть вещественные функции, то есть

.

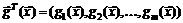Матрицей Якоби 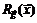m-мерной вектор-функции 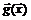называется матрица размера 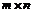, элементы 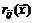которой определяются формулами

.

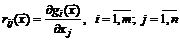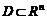Функция называется выпуклой в области , если

, .

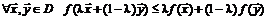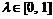Функция называется вогнутой в области 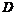, если

, .

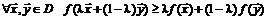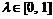Замечание 1.2.Функция является вогнутой в области 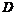, если функция 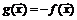выпукла в этой области.

Свойства выпуклых функций

1. Сумма выпуклых функций является выпуклой функцией.

2. Если выпукла и 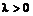, то 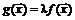тоже выпукла.

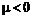3. Если выпукла и , то 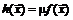вогнута.