Случайные процессы. Марковские случайные процессы.

Переход СМО из одного состояния в другое происходит случайным образом и представляет собой случайный процесс. Работа СМО — случайный процесс с дискретными состояниями, поскольку его возможные состояния во времени можно заранее перечислить. Причем переход из одного состояния в другое происходит скачкообразно, в случайные моменты времени, поэтому он называется процессом с непрерывным временем. Таким образом, работа СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Например, в процессе обслуживания оптовых покупателей на фирме «Кристалл» в Москве можно фиксировать заранее все возможные состояния простейших СМО, которые входят во весь цикл коммерческого обслуживания от момента заключения договора на поставку ликеро-водочной продукции, ее оплаты, оформления документов, отпуска и получения продукции, погрузки и вывоза со склада готовой продукции.

Из множества разновидностей случайных процессов наибольшее распространение в коммерческой деятельности получили такие процессы, для которых в любой момент времени характеристики процесса в будущем зависят только от его состояния в настоящий момент и не зависят от предыстории — от прошлого. Например, возможность получения с завода «Кристалл» ликероводочной продукции зависит от наличия ее на складе готовой продукции, т.е. его состояния в данный момент, и не зависит от того, когда и как получали и увозили в прошлом эту продукцию другие покупатели.

Такие случайные процессы называются процессами без последствия, или марковскими, в которых при фиксированном настоящем будущее состояние СМО не зависит от прошлого. Случайный процесс, протекающий в системе, называется марковским случайным процессом, или «процессом без последствия», если он обладает следующим свойством: для каждого момента времени t₀ вероятность любого состояния t > t₀ системы S_i в будущем (t > t₀) зависит только от ее состояния в настоящем (при t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние, т.е. от того, как развивался процесс в прошлом.

Марковские случайные процессы делятся на два класса: процессы с дискретными и непрерывными состояниями. Процесс с дискретными состояниями возникает в системах, обладающих только некоторыми фиксированными состояниями, между которыми возможны скачкообразные переходы в некоторые, заранее не известные моменты времени. Рассмотрим пример процесса с дискретными состояниями. В офисе фирмы имеются два телефона. Возможны следующие состояния у этой системы обслуживания: S₀ — телефоны свободны; S₁ — один из телефонов занят; S₂ – оба телефона заняты.

Процесс, протекающий в этой системе, состоит в том, что система случайным образом переходит скачком из одного дискретного состояния в другое.

Процессы с непрерывными состояниями отличаются непрерывным плавным переходом из одного состояния в другое. Эти процессы более характерны для технических устройств, нежели для экономических объектов, где обычно лишь приближенно можно говорить о непрерывности процесса (например, непрерывном расходовании запаса товара), тогда как фактически всегда процесс имеет дискретный характер. Поэтому далее мы будем рассматривать только процессы с дискретными состояниями.

Марковские случайные процессы с дискретными состояниями в свою очередь подразделяются на процессы с дискретным временемипроцессы с непрерывным временем. В первом случае переходы из одного состояния в другое происходят только в определенные, заранее фиксированные моменты времени, тогда как в промежутки между этими моментами система сохраняет свое состояние. Во втором случае переход системы из состояния в состояние может происходить в любой случайный момент времени.

На практике процессы с непрерывным временем встречаются значительно чаще, поскольку переходы системы из одного состояния в другое обычно происходят не в какие-то фиксированные моменты времени, а в любые случайные моменты времени.

Для описания процессов с непрерывным временем используется модель в виде так называемой марковской цепи с дискретными состояниями системы, или непрерывной марковской цепью.

Уравнения Колмогорова.

Рассмотрим математическое описание марковского случайного процесса с дискретными состояниями системы S₀, S₁, S₂ (см. рис. 6.2.1) и непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностями l_ij, а обратный переход — под воздействием другого потока l_ij, Введем обозначение р_i как вероятность того, что в момент времени t система находится в состоянии S_i. Для любого момента времени t справедливо записать нормировочное условие — сумма вероятностей всех состояний равна 1:

S p_i(t) = p₀(t) + p₁(t) + p₂(t) = 1.

i=0

Проведем анализ системы в момент времени t, задав малое приращение времени Dt, и найдем вероятность p₁(t + Dt) того, что система в момент времени (t + Dt) будет находиться в состоянии S₁, которое достигается разными вариантами:

а) система в момент t с вероятностью p_i(t) находилась в состоянии S_i и за малое приращение времени Dt так и не перешла в другое соседнее состояние — ни в S₀, ни в S₂. Вывести систему из состояния S₁ можно суммарным простейшим потоком с интенсивностью (l₁₀ + l₁₂) , поскольку суперпозиция простейших потоков также является простейшим потоком. На этом основании вероятность выхода из состояния S₁ за малый промежуток времени Dt приближенно равна (l₁₀ + l₁₂)×Dt. Тогда вероятность невыхода из этого состояния равна [1 — (l₁₀ + l₁₂) × Dt]. В соответствии с этим вероятность того, что система останется в состоянии S₁ на основании теоремы умножения вероятностей, равна:

p₁(t)[l – (l₁₀ + l₁₂)×Dt];

б) система находилась в соседнем состоянии S₀ И за малое время Dt перешла в состояние S₁. Переход системы происходит под воздействием потока l₀₁ c вероятностью, приближенно равной l₀₁ Dt.

Вероятность того, что система будет находиться в состоянии S₁, в этом варианте равна p₀(t) l₀₁Dt;

в) система находилась в состоянии S₂ и за время Dt перешла в состояние S₁ под воздействием потока интенсивностью l₂₁ с вероятностью, приближенно равной l₂₁Dt. Вероятность того, что система будет находиться в состоянии S₁, равна p₂(t)l₂₁Dt.

Применяя теорему сложения вероятностей для этих вариантов, получим выражение:

p₁(t + Dt) = p₁(t)[1 – (l₁₀ + l₁₂ ) Dt] + p₀(t) l₀₁Dt + p₂(t)l₂₁Dt,

которое можно записать иначе:

p₁(t + Dt) – p₁(t) ₌ p₀(t)l₀₁ + p₂(t)l₂₁ – p₁(t)(l₁₀ + l₁₂).

Dt

Переходя к пределу при А/ -^ О, приближенные равенства перейдут в точные, и тогда получим производную первого порядка

dp_{1 =} p₀l₀₁ + p₂l₂₁ – p₁(l₁₀ + l₁₂),

d_t

что является дифференциальным уравнением.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:

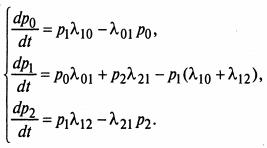
Для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО S_i в функции времени p_i(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы в этом состоянии. Если предельная вероятность состояния S₀ равна p₀ = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S0. Например, при отсутствии заявок на обслуживание k = 0, p0 = 0,2, следовательно, в среднем 2 ч в день система находится в состоянии S₀ и простаивает, если продолжительность рабочего дня составляет 10 ч.

Поскольку предельные вероятности системы постоянны, то, заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО. Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность р_i рассматриваемого состояния S₁ умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) из данного состояния S_i систему, а справа от знака равенства — сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние S_i систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1:

S p_i(t)=1

i=1

Например, для СМО, имеющей размеченный граф из трех состояний S₀, S₁, S₂ рис. 6.2.1, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:

Выходящие Входящие

Для состояния S₀® p₀ – l₀₁ = p₁×l₁₀

Для состояния S₁® (l₁₀ + l₁₂) = p₀l₀₁ + p₁l₂₁

Для состояния S₂® p₂l₂₁ = p₁l₁₂

p₀ + p₁ + p₂ = 1

Пример 1. Составим систему уравнений Колмогорова в общем виде для случая, когда граф состояний имеет вид (рис. 6.2.2):

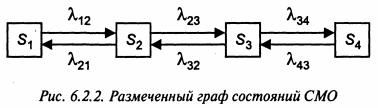
Плотность вероятностей этих переходов указана рядом с соответствующими стрелками. Пользуясь приведенными выше правилами, получаем систему уравнений:

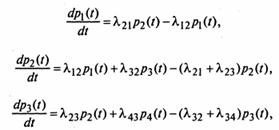
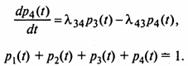
К этим уравнениям надо добавить еще начальные условия. Например, если при t = 0 система S находится в состоянии S₁, то начальные условия можно записать так:

p₁(0) = 1, p₂(0) = p₃(0) = p₄(0) = 0.

Переходы между состояниями СМО происходят под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение времени Dt, т.е. величиной элемента вероятности перехода l_ij Dt, где l_ij — интенсивность потока событий, переводящих систему из состояния / в состояние j (по соответствующей стрелке на графе состояний).

Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет марковским случайным процессом, т.е. процессом без последствия. В этом случае поведение системы достаточно просто определяется, если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все вероятности состояний как функции времени:

p_i(t), p₂(t), …, p_n(t).

Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что существует

Lim p_i(t) = p_i (i = 1,2, …, n)

t®¥

независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t®¥ и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои состояния, но каждое из этих состояний осуществляется с некоторой постоянной вероятностью, определяемой средним временем пребывания системы в каждом из состояний.

Вычислить предельные вероятности состояния p_i можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t®¥ зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему обычных линейных алгебраических уравнений, которая совместно с нормировочным условием позволяет вычислить все предельные вероятности состояний.

Пример 2. Запишем систему алгебраических уравнений для вычисления предельных вероятностей состояний системы, изображенной на рис. 6.2.2.

Для этого допустим, что

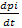= 0 (i = 1; 2; 3; 4),

тогда из записанной ранее в примере 1 системы уравнений Колмогорова получаем:

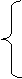l21p23 - l12p1 =0,

l12p1 + l23p^3 - (l21 + l23)p2 =0,

l23p2 + l43p4 -(l32 +l34)p3 =0,

l34p3 - l43p4=0;

И, Кроме того, мы должны учесть нормировочное условие:

p₁+p₂+p₃+p₄=1

Любое из уравнений записанной системы можно исключить, использовав вместо него нормировочное условие.

Вопрос 58. Классификация СМО в коммерческой деятельности (по числу каналов, по характеру расположения, по характеристике каналов).

По числу каналовобслуживания СМО разделяются наодноканальныел = 1 и многоканальные, для которых л > 2. Одноканальные например: выполняемые на рабочем месте операции одним бухгалтером, менеджером, коммерсантом, товароведом, экономистом, торговым аппаратом. В зависимости отвзаимного расположения каналовсистемы подразделяются на СМО спараллельными и с последовательными каналами.В СМО с параллельными каналами входной поток заявок на обслуживание является общим, и поэтому заявки в очереди могут обслуживаться любым свободным каналом, например официантами в ресторане. В таких СМО очередь на обслуживание можно рассматривать как общую. В СМО с последовательным расположением каналов каждый канал может рассматриваться как отдельная одноканальная СМО или фаза обслуживания. Очевидно, выходной поток обслуженных заявок одной СМО является входным потоком для последующей СМО.

В зависимости отхарактеристик каналов обслуживаниямногоканальные СМО подразделяются на СМО соднородными и неоднородными каналами. Отличие состоит в том, что в СМО с однородными каналами заявка потока может обслуживаться любым свободным каналом, а в СМО с неоднородными каналами отдельные заявки обслуживаются только специально для этой

цели предназначенными каналами. В кафе, например, посетитель проходит несколько разных по своему содержанию операций обслуживания, каждая из которых может быть представлена в виде простейшей одноканальной СМО, называемой фазой обслуживания, а в целом весь процесс обслуживания только посетителей может быть представлен в виде структурной модели многофазной СМО.

Вопрос 59. Классификация СМО в коммерческой деятельности (по возможности образования очереди, по характеру очереди, по организации потока заявок, по характеру дисциплины).

СМО в зависимостиот возможности образования очередиподразделяются на два основных типа:СМО с отказамиобслуживания иСМО с ожиданием(очередью) обслуживания. В СМО с отказами возможен отказ в обслуживании, если все каналы уже

заняты обслуживанием, а образовывать очередь и ожидать обслуживание нельзя. В то же время СМО с ожиданием подразделяются на СМО снеограниченным ожиданием, или с неограниченной очередью ИЛИ временем ожидания и СМО сограниченными ожиданиями или очередью, в которых накладываются ограничения на максимально возможную длину очереди или на максимально возможное время пребывания заявки в очереди время работы системы.

Примерами СМО с ограничением на длину очереди: поступление товаров в подсобные помещения, емкости, вместимость которых, естественно, не беспредельна.

Примером СМО с ограничением на время ожидания является обслуживание скоропортящихся товаров, готовых блюд в производстве ресторана, кафе, плодоовощной продукции и продовольственных товаров.

В зависимостиот организации потока заявок СМО подразделяются наразомкнутые и замкнутые. В разомкнутых СМО выходной поток обслуженных заявок не связан с входным потоком заявок на обслуживание и имеет неограниченный источник заявок.

Примером такой системы в коммерческой деятельности является система обслуживания механиками торгового оборудования, которое через некоторое время после ремонта все же опять приходит в неисправное состояние и поступает с заявкой на обслуживание