Геометрическая интерпретация симплекс-метода.

Из приведенных основных теорем ЛП следует, что если задача ЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает. По крайней мере, с одним из допустимых базисных решений системы ограничений:

· Необходимо найти все опорные решения (точки многогранника), множество которых является конечным;

· Вычислить для каждого из опорных решений значения целевой функции

· Сравнить значения целевой функции в каждой из опорных решений и выбрать оптимальное (максимальное или минимальное)

Теоретически данная схема приведет к нахождению оптимального решения, но практически её осуществление связано с большими вычислительными трудностями. Даже в задаче с двумя переменными число опорных решений может оказаться очень большим, а при большом значении n оно может достигать огромных чисел и практическое осуществление указанного перебора всех опорных решений станет невозможным. Эти вычисленные трудности возникают в результате того, что рассмотренная принципиальная схема связана с простым перебором опорных решений, т.е. в этой схеме не принимается во внимание тот факт, на сколько новое испытуемое опорное решение улучшает значение решения целевой функции и приближает нас к оптимальному решению. Если же указанный перебор опорных решений производить направлении., т.е. на каждом из шагов улучшая ( или, по крайней мере, не ухудшая) значения целевой функции то число перебираемых опорных решений можно резко сократить, что в конечном итоге приводит к весьма существенному сокращению числа шагов при отыскивании оптимума целевой функции. При использовании такой схемы, в отличие от первой, каждое последующее опорное решение выбирается таким образом, чтобы оно было лучше, (или по крайней мере, не хуже) предыдущего. Именно на каждом из шагов значение целевой функции улучшается ( или, по крайней мере, не ухудшается).

Сравним результаты применения схем простого и направленного перебора на конкретном примере.

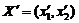Рассмотрим случай, когда область допустимых решений задачи ЛП (рис.1) представлена замкнутым выпуклым многоугольником ABCDEGH. Предположим, что первым из базисных решений которое найдено, является вектор ,компоненты которого соответствуют координатам угловой точки А рассматриваемого многоугольника. При использовании схемы прямого перебора решений, мы, последовательно переходя от вершины к вершине ( начиная от вершины А и заканчивая вершиной Н), вынуждены бы были испытать все семь вершин многоугольника. Предположим, что применение данного способа позволило нам определить. Что оптимум достигается в точке С.

Из чертежа видно, что, применяя метод направленного перебора, мы от вершины А перешли бы к вершине В, а затем к оптимальной вершине С, перебрав таким образом всего 3 точки, (вместо 7. Которые мы должны были бы испытать, используя метод простого перебора).

В то же время очевидно, что для практического применения метода направленного перебора необходимо знать:

· Алгоритм определения какого-либо первоначального допустимого решения задачи

· Алгоритм перехода к лучшему ( или, точнее, не к худшему) решению

· Признак, указывающий на , то, что найденое решение относительно.

Фундаментом универсального метода решения задач ЛП. Который называется симплекс-методом, является метод направленного перебора.

Геометрическая интерпретация симплекс-метода состоит в последовательном переходе от одной вершины многогранника к другой ( от первоначально выбранной вершины к одной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее или, по крайней мере, не худшее значение). Этот процесс происходит до тех пор, пока не будет найдено оптимальное решение-вершина, где достигается оптимальное оптимальное решение-вершина, где достигается оптимальное значение функции (если задача имеет конечный оптимум).

Идея симплекс-метода разработана русским учёным Л.В. Канторовичем в 1939 году. На основе этой идеи американский учёный Д.Данциг в 1949 году разработал симплекс-метод, позволяющий решать любую задачу ЛП.

В настоящее время на основе этого метода разработан пакет программ с применением которого решается задачи ЛП.

Рис. 1.Геометрическая интерпретация симплекс-метода.

19. Метод Гомори. Целочисленное решение(НЕУВЕРЕНА!!!!!))

Значительная часть задач коммерческой деятельности требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например распределение товаров между коммерческими предприятиями, раскрой материалов, число станков при загрузке оборудования, распределение транспортных средств по рейсам, распределение коммерческих заказов между оптовыми предприятиями, продажа автомобилей, распределение самолетов по авиалиниям, количество вычислительных машин в управляющем комплексе и др. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования. Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включает дополнительное требование, состоящее в том, что значения переменных должны быть целыми неотрицательными числами, например, х1 = 30 станков, х2 = 16 самолетов, х3= 7 человек. Методы целочисленной оптимизации можно разделить на три основные группы: а) методы отсечения; б) комбинированные методы; в) приближенные методы. Рассмотрим один из методов отсечения — метод Гомори. Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: а) оно должно быть линейным; б) должно отсекать найденный оптимальный нецелочисленный план; в) не должно отсекать ни одного целочисленного плана. Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Алгоритм Гомори, основанный на симплексном методе, имеет простой способ построения правильного отсечения и содержит следующие этапы. 1. Задача линейного программирования решается без учета условия целочисленности симплексным или двойственным симплексным методом. Если все элементы оптимального плана целые числа, то решение заканчивается для задачи целочисленного программирования. 2. Если среди элементов оптимального решения есть нецелые числа, то необходимо выбрать элемент с наибольшей дробной частью и составить дополнительное ограничение (сечение), которое отсекает нецелочисленные решения. Дополнительное ограничение дается в том случае, если значение базисной переменной в оптимальном плане xi=bi — дробное число. Тогда некоторые элементы аij в i-й строке симплексной таблицы также дробные числа. Обозначим [bi] и [аij] целые части чисел bi и аij, т.е. наибольшие целые числа, не превышающие bi и aij. Величины дробных частей qi и qij определяются как разности следующим образом: qi = bi - [bi]; qij =аij - [aij] и являются положительными числами. Тогда неравенство qi-qi1 x1 - qi2x2 - ... - qimxn £ 0, сформированное по i-й строке симплексной таблицы обладает всеми свойствами правильного отсечения. Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу. 4. Полученная расширенная задача решается двойным симплексным методом. Если новый оптимальный план будет целочисленным, то задача решена. В противном случае необходимо вернуться к п. 2 алгоритма. Если в процессе решения в симплексной таблице появится уравнение с нецелым свободным членом bi и целыми коэффициентами aij, то данная задача не имеет целочисленного оптимального решения. Пример. Маркетинговые исследования указали на необходимость освоения выпуска новой продукции. Поэтому на предприятии решено установить новое технологическое оборудование на освободившейся площади 10 м2. На приобретение оборудования двух видов выделено 6 млн. руб. Комплект первого вида оборудования стоимостью 1 млн руб. устанавливается на площади 5 м2 и позволяет увеличить доход предприятия на 8 млн руб. Комплект второго вида оборудования занимает площадь 2 м2, стоит 1 млн руб. и обеспечивает увеличение дохода предприятия на 5 млн руб. Определите, какое количество технологического оборудования каждого вида следует закупить, чтобы обеспечить максимальное увеличение дохода предприятия от продажи выпускаемой продукции.

20. Двойственная задача линейного программирования и ее математическая модель.(не до конца!!!!)

С каждой задачей ЛП связана другая задача. Название двойственной по отношению к исходной, заметим, что часто говорят о взаимодвойственных задачах т.к. если для исходной построена двойственная, а затем для неё так же построена двойственная, то получится исходная задача.

Рассмотрим пары взаимодвойственных задач позволяет решать ряд проблем:

1) Выбрать наиболее простой способ решения одной задачи, а из него найти решение другой задачи.

2) Рассматривая экономическую интерпретацию двойственных задач можно дать трактовку не только основным и дополнительным переменным, а ещё получить ряд дополнительных соотношений для прогноза и планирования, п и измененных условиях.

21. Виды двойственных задач. Правила составления симметричных двойственных задач линейного программирования.

Можно рассмотреть 2 вида двойственных задач:

- симметричный

- несимметричный

+ смешанный

Для симметричных двойственных задач характерно задание системы ограничений в виде системы неравенств.

Пусть прямая задача имеет вид:

F(x) = C₁x₁+C₂X₂+…+C_nX_n → max (в матрице после вертикальной границы вертикально стоят y1,y2,…,ym)

a₁₁x₁+a₁₂x₂+…+a_1nx_n≤b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n≤b₂

……………………………

a_m1x₁+a_m2x₂+…+a_mnx_n≤b_m

xj≥0 j=1,n

Правило составления симметричной двойственной задачи ЛП.

1. каждому неравенству системы ограничений прямой задачи соответствует 1 переменная двойственной задачи Y=(y₁, y₂, …, y_m) – вектор переменных двойственной задачи. Если в прямой задаче система ограничений содержит m строк, то в двойственной задаче будет m переменных.

2. коэффициенты системы ограничений двойственной задачи получаются путем транспонирования матрицы коэффициентов прямой задачи 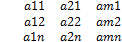(здесь между 2 и 3 строчкой строка точек)

3. столбец свободных членов двойственной задачи состоит из коэффициентов целевой функции прямой задачи С1, С2, …, Сn.

4. коэффициентами целевой функции двойственной задачи служат элементы столбца свободных членов прямой задачи b1, b2, …,bm

5. знаки неравенств в системе ограничений двойственной задачи противоположны знакам неравенств прямой задачи (сохраняя при этом строгость)

6. экстремумы взаимодвойственных задач противоположны, т.е. если прямая задача на max, то двойственная на min. И наоборот.

7. для симметричных задач все переменные и прямой и двойственной задачи неотрицательны.

Таким образом, с учетом правил, симметричная двойственная задача примет вид

Z(Y)= b₁y₁+b₂y₂+…+b_my_m→min

a₁₁y₁+a₂₁y₂+…+a_m1y_m≥c₁

a₁₂y₂+a₂₂y₂+…+a_m2y_m≥c₂

………………………………

a_1ny₁+a_2ny₂+…+a_mny_m≥c_n

yi≥0, i=1,m

22. Виды двойственных задач. Правила составления несимметричных двойственных задач линейного программирования.

Можно рассмотреть 2 вида двойственных задач:

- симметричный

- несимметричный

+ смешанный

В несимметричном случае одна из задач представлена в канонической форме. (в матрице после вертикальной границы вертикально стоят y1,y2,…,ym)

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n=b₂

……………………………

a_m1x₁+a_m2x₂+…+a_mnx_n=b_m

xj≥0 j=1,n

!!! Основные правила составления двойственной задачи те же, что и в симметричном случае. Отличаются пункты 5 и 7.

5. Если в целевой функции двойственной задачи требуется найти max, то в системе ограничений будут содержаться неравенства вида ≤. А если двойственная задача на min, то ≥.

7. т.к. в прямой задаче в системе ограничений содержатся только уравнения, то в двойственной задаче условия неотрицательности отсутствуют. Т.е. yi – произвольно изменяющаяся переменная.

Таким образом для указанной прямой задачи двойственная задача примет вид:

Z(Y)= b₁y₁+b₂y₂+…+b_my_m→min

a₁₁y₁+a₂₁y₂+…+a_m1y_m≥c₁

a₁₂y₂+a₂₂y₂+…+a_m2y_m≥c₂

………………………………

a_1ny₁+a_2ny₂+…+a_mny_m≥c_n

yi≥0, i=1,m

23. Основное неравенство теории двойственности. Достаточный признак оптимальности. Первая теорема двойственности.

Основное неравенство теории двойственности: для любых допустимых решений пары взаимодвойственных задач X(x1, x2,…,xn), Y(y1,y2,…,ym) справедливо неравенство F(X)≤Z(Y)

Достаточный признак оптимальности:

если X*=(x*1,x*2,…,x*n) и Y*=(y*1,y*2,…,y*m) – допустимые решения задач, для которых выполняется условие F(X*)=Z(Y*), то X* и Y* - оптимальные решения двойственных задач!

Первая основная теорема двойственности:

если одна из взаимодвойственных задач имеет оптимальное решение, то другая задача также имеет оптимальное решение, причем для любых оптимальных решений X* и Y* выполняется равенство F(X*)=Z(Y*). Обратное утверждение тоже справедливо. Однако, если одна из двойственных задач не имеет решения вследствие ограниченности целевой функции F(X)→∞, то другая задача не будет иметь решения вследствие несовместности системы ограничений. Обратное утверждение не всегда верно, т.е. если задача имеет несовместную систему ограничений, то двойственная к ней может быть как неограниченной, так и ограниченной.