Дифференцирование сложных функций

I. Пусть .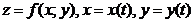

Тогда 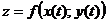есть сложная функция независимой переменнойt.

Пример 5.2.1. Найти 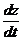, если 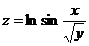, где .

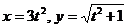▲ Сложная функция z зависит от одной переменной t через промежуточные переменные x и y, которые в свою очередь зависят от одной переменной t. Поэтому полная производная данной функции

.

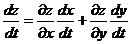Найдем 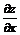, считая y постоянной (тогда )

.

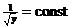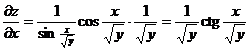Считая x постоянной, имеем

.

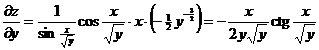Найдем :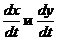

.

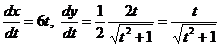В соответствии с приведенной выше формулой

.

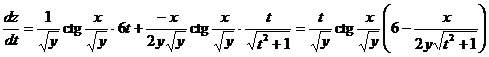Подставив в полученное выражение вместо промежуточных переменных x и y соответственно 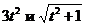, окончательно получим

. ▼

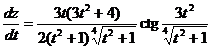В частном случае, когда 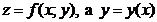, и, следовательно, z является сложной функцией 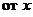, 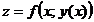. На основании предыдущей формулы, в которой роль t играет теперь x, получим

.

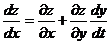В данной формуле 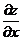есть частная, или локальная, производная функции 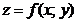по переменной x.

А 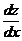есть полная, или материальная производная функции 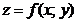по переменной x.

Пример 5.2.2. Найти 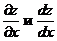, если .

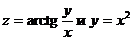▲ Считая y постоянной, находим

.

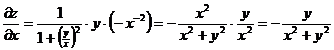Полная производная данной функции z

.

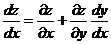Считая x (тогда 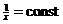) постоянной, имеем

.

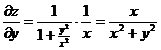Найдем 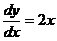. В соответствии с формулой для полной производной данной функции имеем

.

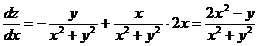Подставляя в полученное выражение 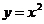, окончательно получим

. ▼

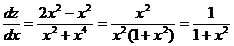Пример 5.2.3. Найти 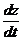, если 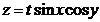, где .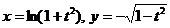

▲ Функция z есть функция трех переменных 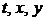. Однако x и y являются функциями одной переменной t. Поэтому формула полной производной функции z в данном случае имеет вид

.

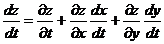Найдем частные производные функции 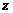по переменным .

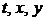Считая x и y постоянными (тогда 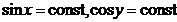), находим

.

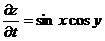Считая t и y постоянными (тогда 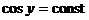), имеем

.

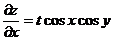Считая t и x постоянными (тогда 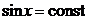), получим

.

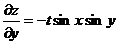Найдем :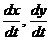

.

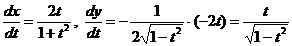Согласно приведенной выше формуле, имеем

.

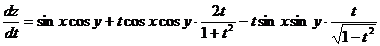В полученное выражение вместо переменных x и y необходимо подставить соответственно . ▼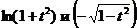

II. Пусть .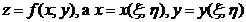

Тогда 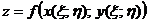есть сложная функция независимых переменных .

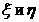Если сложная функция 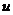задана формулами

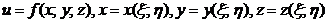
то .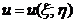

? ? ?

Правилодифференцирования сложной функции:

Частная производная сложной функции по одной из независимых переменных равна

Сумме произведений ее частных производных по промежуточным аргументам на частные производные этих аргументов по данной независимой переменной.

! ! !

Пример 5.2.4. Найти частные производные функции 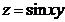, где .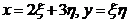

▲ Частные производные сложной функции z, зависящей от двух промежуточных переменных x и y, которые в свою очередь зависят от независимых переменных, ξ и η находим по формулам

;

.

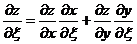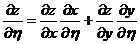Получаем:

;

.

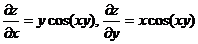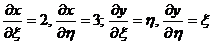В соответствии с приведенными формулами имеем

,

.

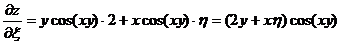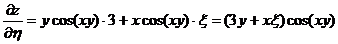Подставив в полученные выражения вместо переменных x и y соответственно

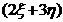и ,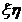

окончательно получим

,

. ▼

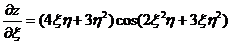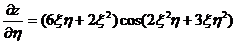Дифференцирование неявных функций

Пример 5.3.1. Найти производную неявной функции 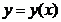, заданной уравнением

.

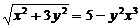▲ Преобразуем данное уравнение к виду

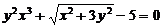
и рассмотрим функцию

.

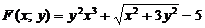Тогда по формуле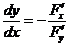

.

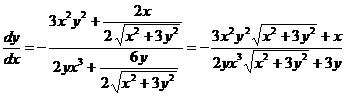Так как по условию 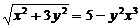, то можно упростить

. ▼
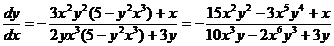