Понятие функции нескольких переменных

Пусть E есть область изменения независимых переменных x и y.

Переменная z называется функцией независимых переменныхx и yна множествеE, если каждой упорядоченной паре чисел соответствует определенное значение z. Множество E пар чисел 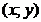, на котором определена функция, называется областью определения, или областью существования функции.

Символически функция двух переменных записывается в виде одного из равенств

и т. д.

В первом из этих равенств f обозначает закон соответствия. Этот закон может быть задан аналитически (формулой), с помощью таблицы или графика. Так как всякое уравнение 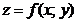определяет, вообще говоря, в пространстве, в котором введена, декартова система координат Oxyz, некоторую поверхность, то под графиком функции двух переменных будем понимать поверхность, образованную множеством точек , координаты которых удовлетворяют уравнению .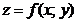

Геометрически область определения функции E обычно представляет собой некоторую часть плоскости Oxy, ограниченную линиями, которые могут принадлежать или не принадлежать этой области. В первом случае область E называется замкнутой и обозначается , во втором – открытой.

Частное значение функции 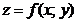в точке 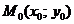обозначается 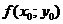или .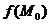

Определение функции двух переменных легко обобщается на случай трех и большего числа переменных.

Переменная величина 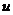называется функцией трех переменных величин 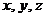, если каждой упорядоченной тройке значений 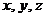соответствует определенное значение .

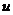Обозначение: 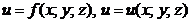и т. д.

Величина y называется функцией упорядоченных переменных , если каждой совокупности 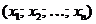переменных из некоторой области n-мерного пространства соответствует определенное значение y, что символически записывается в виде .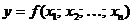

Так как совокупность значений независимых переменных определяет точку n-мерного пространства , то всякую функцию нескольких переменных обычно рассматривают как функцию точек M пространства соответствующей размерности: .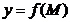

Линией уровня функции 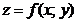называется множество точек плоскости Oxy, для которых данная функция имеет одно и то же значение.

Уравнение линии уровня есть .

Поверхностью уровня функции трех переменных 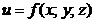называется множество точек пространства Oxyz, для которых данная функция имеет одно и то же значение, т. е.

.

Частное и полное приращение

Пусть функция 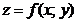определена в некоторой области E на плоскости Oxy. Одной из основных задач теории функций нескольких переменных является задача исследования данной функции.

Возьмем внутреннюю точку 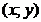из области E и дадим x приращение 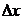такое, чтобы точка .

Величина

называется частным приращением функцииzпо переменнойx.

Возьмем внутреннюю точку 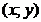из области E и дадим y приращение , такое, чтобы точка .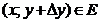

Величина

называется частным приращением функцииzпо переменнойy.

Возьмем внутреннюю точку 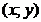из области E и дадим переменным x и y соответственно приращения , такие, чтобы точка .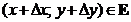

Величина

называется полным приращением функцииz.

Частные приращения функции 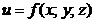определяются формулами:

;

;

.

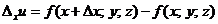Полное приращение функции :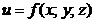

.

Аналогично определяются частные приращения функции n переменных.

Например,

.

Полное приращение функции n переменных:

.