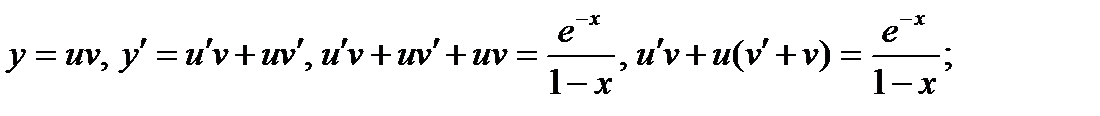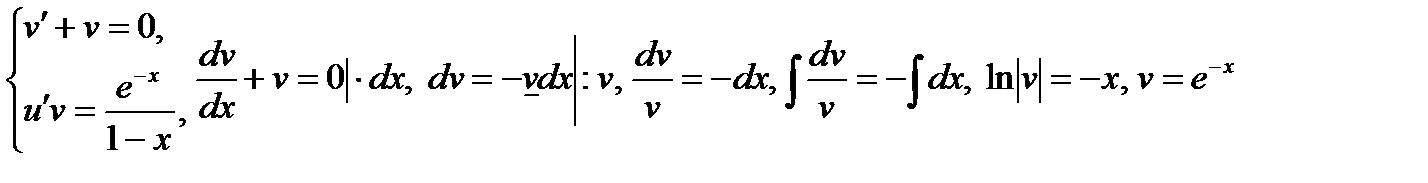Однородные линейные дифференциальные уравнения
Однородные линейные дифференциальные уравнения
Высших порядков.
Однородные уравнения с постоянными коэффициентами
Пример.2.3.1. Найти частное решение уравнения  , если
, если
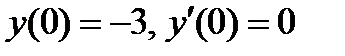 .
.
▲ Чтобы решить задачу Коши, то есть определить частное решение уравнения 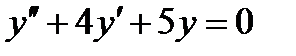 по заданным условиям
по заданным условиям 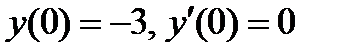 , нужно:
, нужно:
1. Найти общее решение:
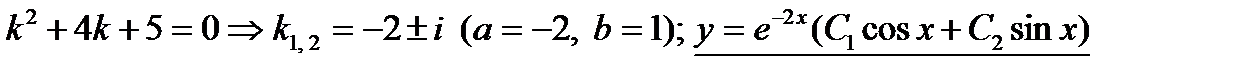 .
.
2. Подставить начальное условие  в общее решение
в общее решение
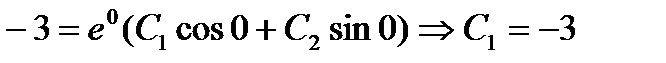 .
.
3. Найти 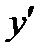 от общего решения и подставить туда второе начальное условие:
от общего решения и подставить туда второе начальное условие:  .
.
 ,
,
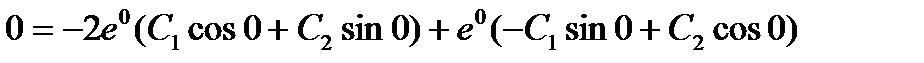 .
.
4. Решить полученную для определения  систему
систему
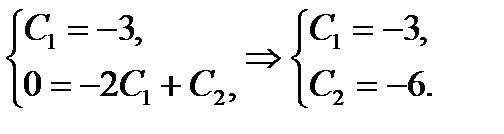
5. Подставить  в общее решение:
в общее решение:
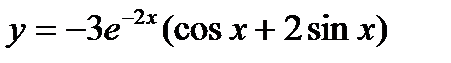 − частное решение. ▼
− частное решение. ▼
Неоднородные дифференциальные уравнения второго порядка
Уравнения с разделяющимися переменными
Решить следующие дифференциальные уравнения (найти их общие интегралы):
1.  . Ответ:
. Ответ: 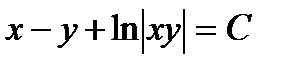 .
.
2.  . Ответ:
. Ответ: 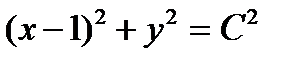 .
.
3. 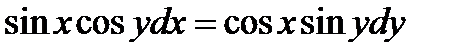 . Ответ:
. Ответ: 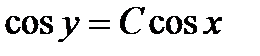 .
.
4. 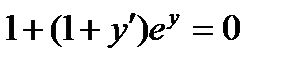 . Ответ:
. Ответ: 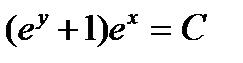 .
.
5. 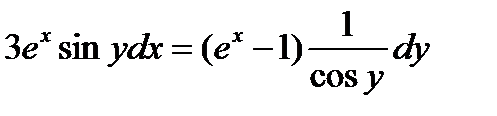 . Ответ:
. Ответ: 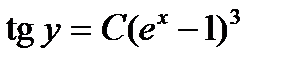 .
.
6. 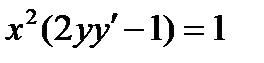 . Ответ:
. Ответ:  .
.
Найти частные решения следующих уравнений при указанных начальных условиях:
7. 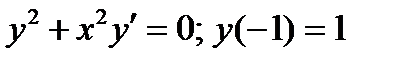 . Ответ:
. Ответ: 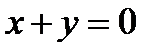 .
.
8. 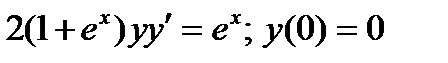 . Ответ:
. Ответ:  .
.
9.  . Ответ:
. Ответ: 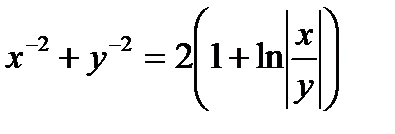 .
.
Однородные уравнения 1-го порядка
Решить следующие уравнения:
1.  . Ответ:
. Ответ:  .
.
2. 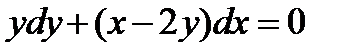 . Ответ:
. Ответ: 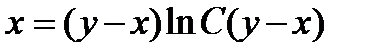 .
.
3.  . Ответ:
. Ответ: 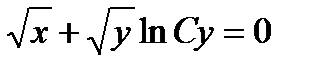 .
.
4. 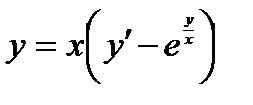 . Ответ:
. Ответ: 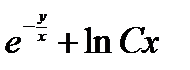 .
.
5.  . Ответ:
. Ответ: 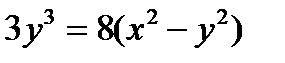 .
.
Линейные уравнения 1-го порядка и уравнения Бернулли
1.  . Ответ:
. Ответ: 
2. 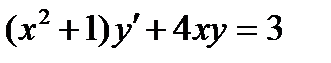 . Ответ:
. Ответ:  .
.
3. 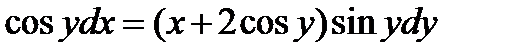 . Ответ:
. Ответ: 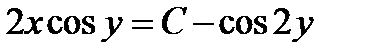 .
.
4. 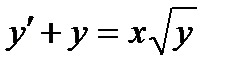 . Ответ:
. Ответ: 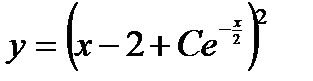 .
.
5.  . Ответ:
. Ответ:  .
.
Уравнения в полных дифференциалах
Проверить, что следующие уравнения 1-го порядка есть уравнения в полных дифференциалах и решить их:
1.  . Ответ:
. Ответ: 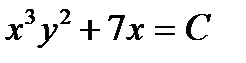 .
.
2.  . Ответ:
. Ответ:  .
.
3. 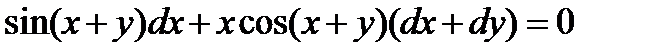 . Ответ:
. Ответ:  .
.
4. 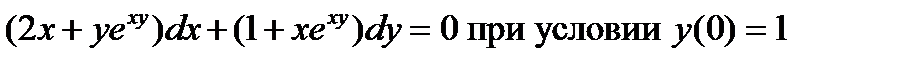 . Ответ:
. Ответ: 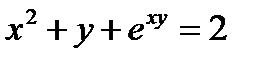 .
.
Уравнения высших порядков, допускающие понижение порядка
Решить уравнения:
1.  . Ответ:
. Ответ:  .
.
2. 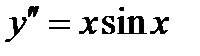 . Ответ:
. Ответ: 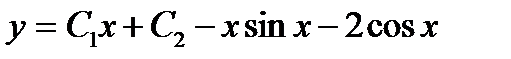 .
.
3. 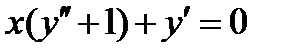 . Ответ:
. Ответ: 
4. 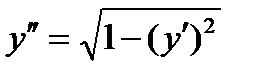 . Ответ:
. Ответ: 
5.  . Ответ:
. Ответ: 
6. 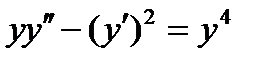 . Ответ:
. Ответ:  .
.
Найти частное решение данного уравнения, удовлетворяющее указанным начальным условиям:
7.  . Ответ:
. Ответ: 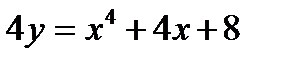 .
.
8.  . Ответ:
. Ответ:  .
.
9.  . Ответ:
. Ответ:  .
.
Однородные линейные дифференциальные уравнения
С постоянными коэффициентами
Найти общие решения уравнений:
1.  . Ответ:
. Ответ:  .
.
2. 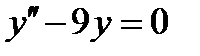 . Ответ:
. Ответ:  .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ:
. Ответ: 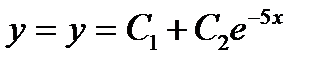 .
.
5.  . Ответ:
. Ответ: 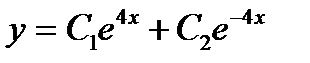 .
.
6.  . Ответ:
. Ответ: 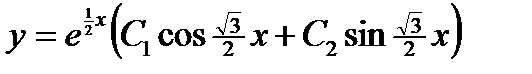 .
.
7. 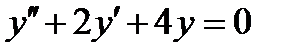 . Ответ:
. Ответ:  .
.
8. 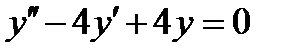 . Ответ:
. Ответ:  .
.
9. 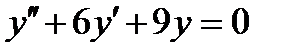 . Ответ:
. Ответ:  .
.
10.  . Ответ:
. Ответ:  .
.
11.  . Ответ:
. Ответ:  .
.
12. 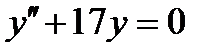 . Ответ:
. Ответ: 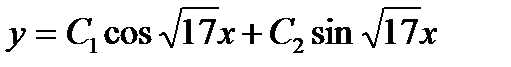 .
.
Неоднородные линейные дифференциальные уравнения
С постоянными коэффициентами
Найти общие решения уравнений:
1.ч  . Ответ:
. Ответ:  .
.
2. 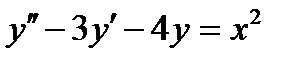 . Ответ:
. Ответ:  .
.
3.  . Ответ:
. Ответ: 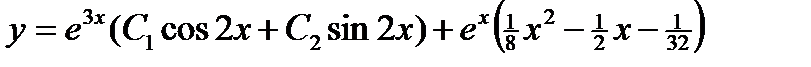 .
.
4. 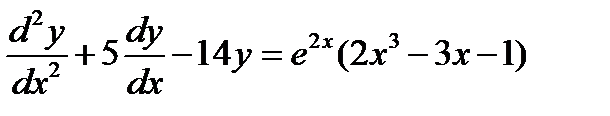 .Ответ:
.Ответ: 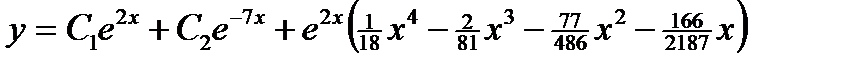 .
.
5.  . Ответ:
. Ответ: 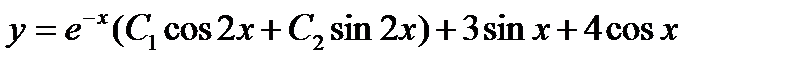 .
.
6.  . Ответ:
. Ответ: 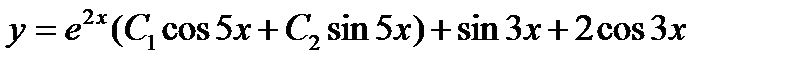 .
.
7.  .
.
Ответ: 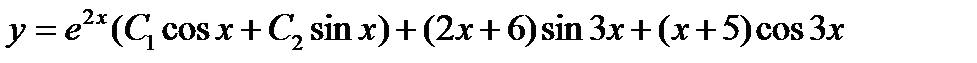 .
.
ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ
1-3. Найти общее решение (общий интеграл) дифференциального уравнения.
4. Найти частное решение (частный интеграл) дифференциального уравнения.
5. Найти общее решение дифференциального уравнения.
6. Найти частное решение дифференциального уравнения и вычислить значение полученной функции  при данном значении x с точностью до двух знаков после запятой.
при данном значении x с точностью до двух знаков после запятой.
7. Найти общее решение дифференциального уравнения, допускающего понижение порядка.
8. Решить задачу Коши для дифференциального уравнения, допускающего понижение порядка.
9-11. Найти общее решение дифференциального уравнения.
12. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
ВАРИАНТ 1 1. 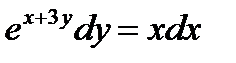 . 2. . 2.  . 3. . 3.  . 4. . 4.  . 5. . 5. 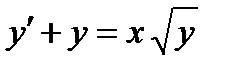 6. 6.  ; ;  7. 7.  . 8. . 8. 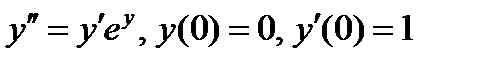 . 9. a. . 9. a. 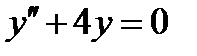 ; б) ; б) 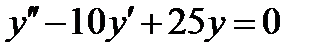 ; в) ; в) 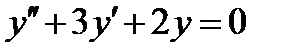 . 10. . 10.  . 11. . 11. 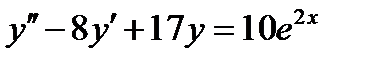 . 12. . 12.  ; ; 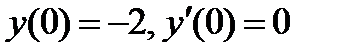 . . | ВАРИАНТ 2 1.  . 2. . 2.  . 3. . 3. 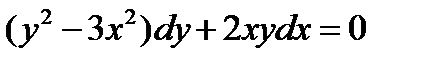 . 4. . 4. 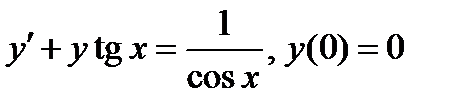 . 5. . 5. 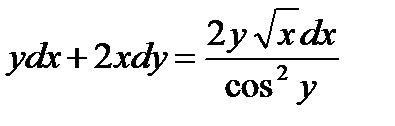 . 6. . 6. 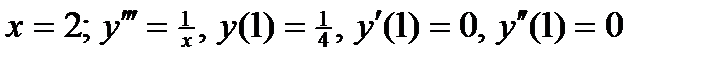 . 7. . 7.  . 8. . 8. 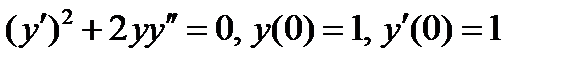 . 9. а) . 9. а)  ; б) ; б)  ; в) ; в)  . 10. . 10.  . 11. . 11. 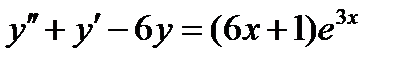 . 12. . 12. 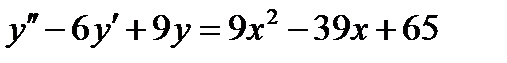 ; ;  . . |
ВАРИАНТ 3 1.  . 2. . 2.  . 3. . 3.  . 4. . 4.  . 5. . 5.  . 6. . 6. 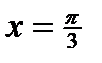 ; ; 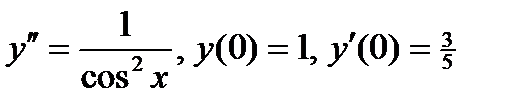 . 7. . 7. 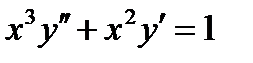 . 8. . 8.  . 9. а) . 9. а)  ;б) ;б)  ; в) ; в)  . 10. . 10. 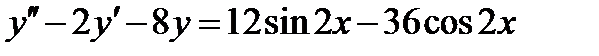 . 11. . 11.  . 12. . 12.  , ,  . . | ВАРИАНТ 4 1.  . 2. . 2. 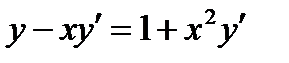 . 3. . 3. 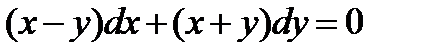 . 4. . 4.  . 5. . 5. 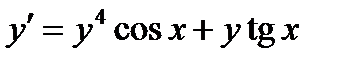 . 6. . 6.  . 7. . 7.  . 8. . 8. 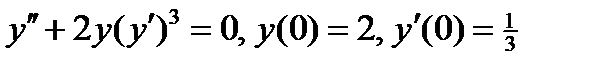 . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 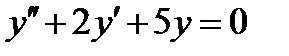 . 10. . 10. 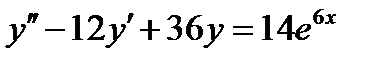 . 11. . 11.  . 12. . 12.  , ,  . . |
ВАРИАНТ 5 1. 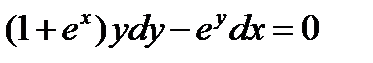 . 2. . 2. 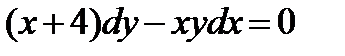 . 3. . 3. 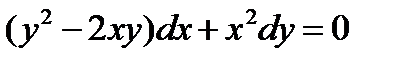 . 4. . 4.  . 5. . 5.  . 6. . 6. 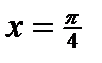 ; ; 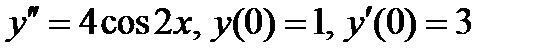 . 7. . 7.  . 8. . 8.  . 9. а) . 9. а) 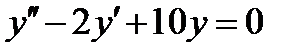 ; б) ; б) 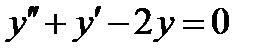 ; в) ; в) 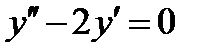 . 10. . 10.  . 11. . 11.  . 12. . 12. 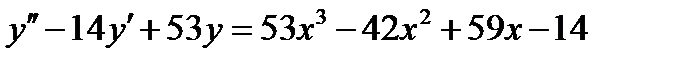 , , 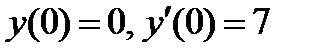 . . | ВАРИАНТ 6 1. 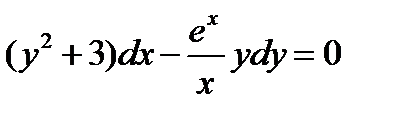 . 2. . 2. 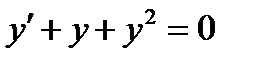 . 3. . 3.  . 4. . 4.  . 5. . 5. 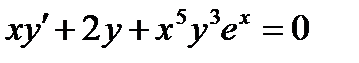 . 6. . 6. 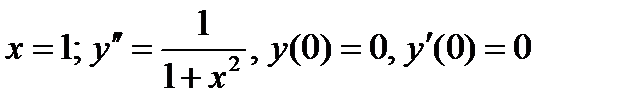 . 7. . 7. 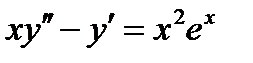 . 8. . 8. 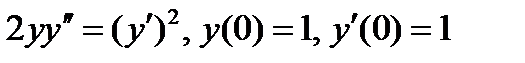 . 9. а) . 9. а)  ; б) ; б)  ; в) ; в)  . 10. . 10. 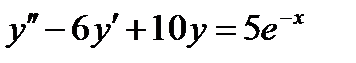 . 11. . 11. 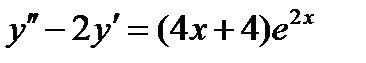 . 12. . 12.  , , 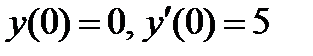 . . |
ВАРИАНТ 7 1. 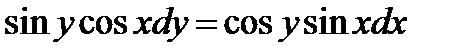 . 2. . 2. 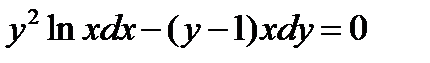 . 3. . 3.  . 4. . 4. 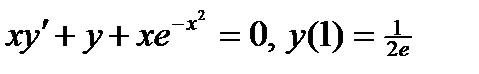 . 5. . 5.  . 6. . 6. 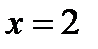 ; ; 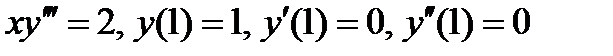 . 7. . 7. 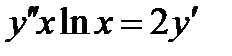 . 8. . 8.  . 9. а) . 9. а)  ; б) ; б) 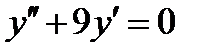 ; в) ; в)  . 10. . 10. 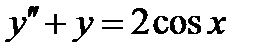 . 11. . 11. 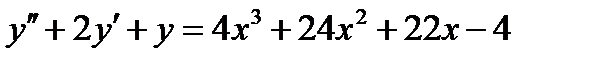 . 12. . 12. 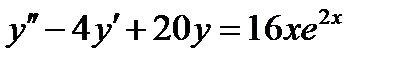 , ,  . . | ВАРИАНТ 8 1.  . 2. . 2.  . 3. . 3. 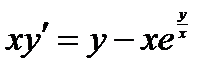 . 4. . 4.  . 5. . 5.  . 6. . 6.  7. 7.  . 8. . 8.  . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 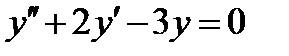 . 10. . 10. 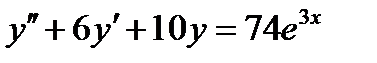 . 11. . 11.  . 12. . 12.  , , 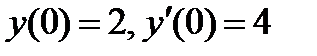 . . |
ВАРИАНТ 9 1.  . 2. . 2. 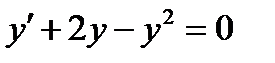 . 3. . 3.  . 4. . 4.  . 5. . 5. 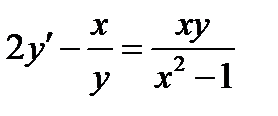 . 6. . 6. 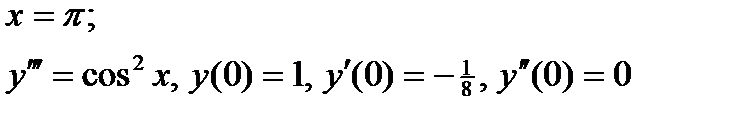 7. 7.  . 8. . 8.  . 9. а) . 9. а)  ; б) ; б) 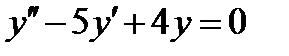 ; в) ; в) 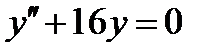 . 10. . 10. 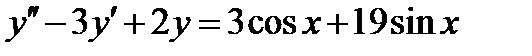 . 11. . 11.  . 12. . 12.  , ,  . . | ВАРИАНТ 10 1.  . 3. . 3.  . 2. . 2. 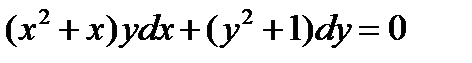 . 4. . 4.  . 5. . 5. 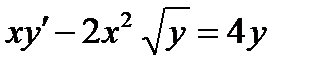 . 6. . 6.  . 7. . 7. 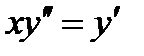 . 8. . 8.  . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 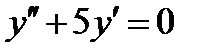 . 10. . 10. 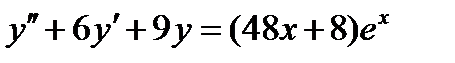 . 11. . 11. 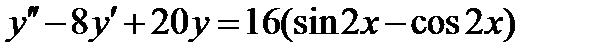 . 12. . 12.  , , 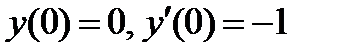 . . |
ВАРИАНТ 11 1. 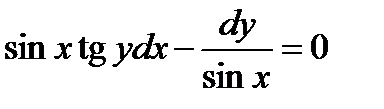 . 2. . 2. 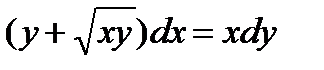 . 3. . 3. 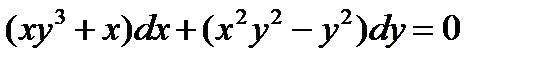 . 4. . 4.  . 5. . 5.  . 6. . 6.  ; ; 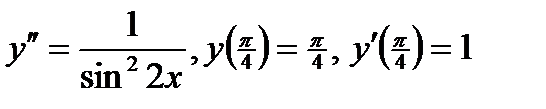 . 7. . 7. 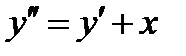 . 8. . 8. 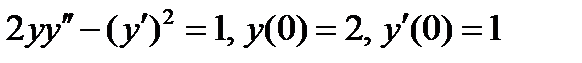 . 9. а) . 9. а) 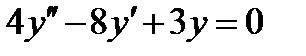 ; б) ; б)  ; в) ; в) 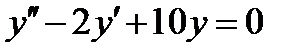 . 10. . 10. 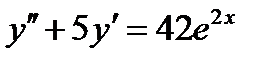 . 11. . 11.  . 12. . 12. 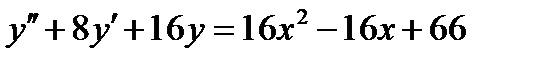 , ,  . . | ВАРИАНТ 12 1. 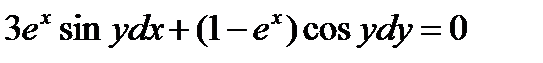 . 2. . 2.  . 3. . 3. 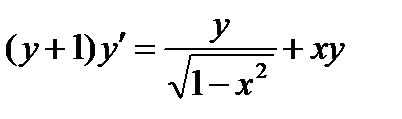 . 4. . 4. 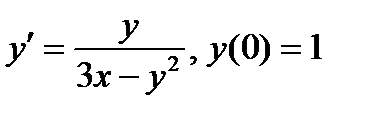 . 5. . 5. 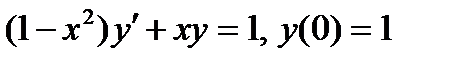 . 6. . 6. 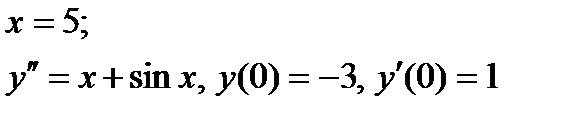 . 7. . 7. 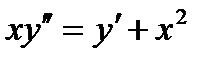 . 8. . 8.  . 9. а) . 9. а) 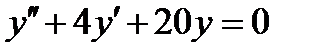 ; б) ; б) 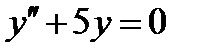 ; в) ; в) 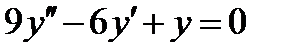 . 10. . 10.  . 11. . 11. 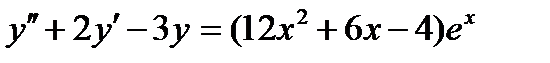 . 12. . 12. 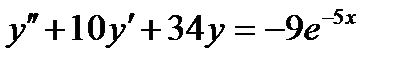 , ,  . . |
ВАРИАНТ 13 1. 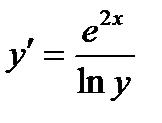 . 3. . 3. 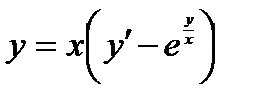 . 2. . 2. 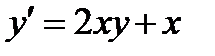 . 4. . 4. 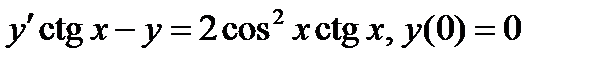 . 5. . 5.  . 6. . 6. 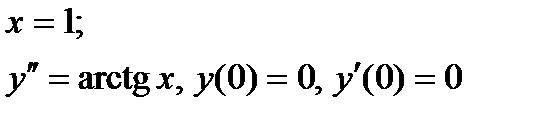 7. 7. 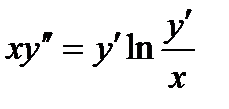 . 8. . 8. 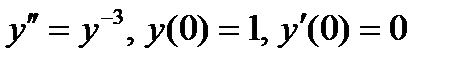 . 9. а) . 9. а) 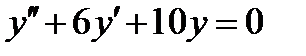 ; б) ; б) 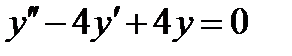 ; в) ; в) 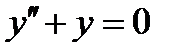 . 10. . 10.  . 11. . 11. 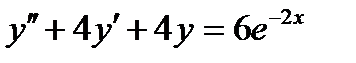 . 12. . 12.  , , 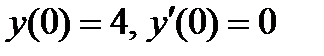 . . | ВАРИАНТ 14 1. 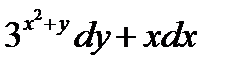 . 2. . 2.  . 3. . 3. 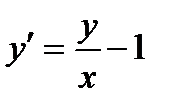 . 4. . 4.  . 5. . 5. 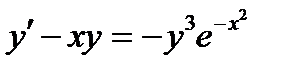 . 6. . 6.  . 7. . 7. 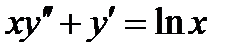 . 8. . 8.  . 9. а) . 9. а) 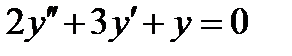 ; б) ; б)  ; в) ; в) 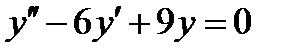 . 10. . 10.  . 11. . 11.  . 12. . 12.  , , 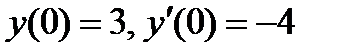 . . |
ВАРИАНТ 15 1. 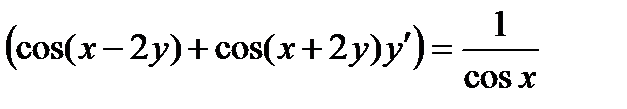 . 2. . 2. 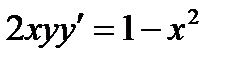 . 3. . 3. 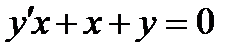 . 4. . 4.  . 5. . 5. 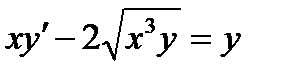 . 6. . 6. 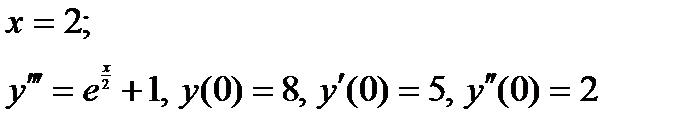 7. 7. 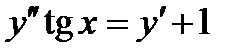 . 8. . 8.  . 9. а) . 9. а) 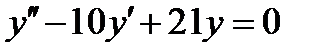 ; б) ; б) 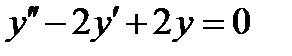 ; в) ; в)  . 10. . 10.  . 11. . 11. 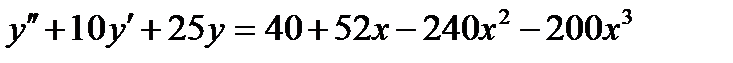 . 12. . 12.  , , 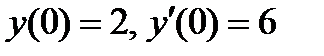 . . | ВАРИАНТ 16 1.  . 2. . 2. 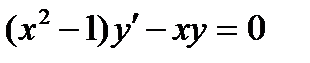 . 3. . 3.  . 4. . 4. 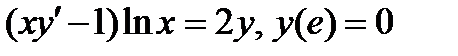 . 5. . 5.  . 6. . 6. 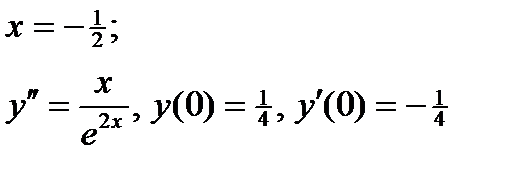 7. 7.  . 8. . 8.  . 9. а) . 9. а) 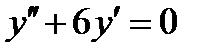 ; б) ; б) 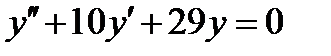 ; в) ; в)  . 10. . 10. 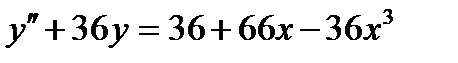 . 11. . 11. 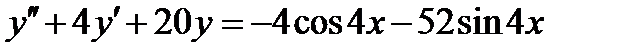 . 12. . 12.  , ,  . . |
ВАРИАНТ 17 1. 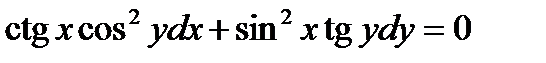 . 2. . 2. 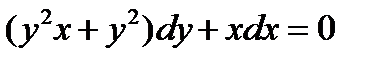 . 3. . 3.  . 4. . 4.  . 5. . 5.  . 6. . 6. 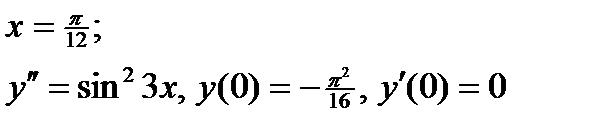 7. 7. 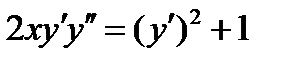 . 8. . 8.  . 9. а) . 9. а) 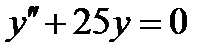 ; б) ; б)  ; в) ; в)  . 10. . 10.  . 11. . 11. 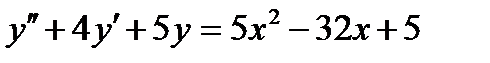 . 12. . 12. 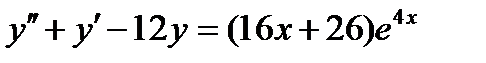 , ,  . . | ВАРИАНТ 18 1. 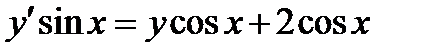 . 2. . 2.  . 3. . 3.  . 4. . 4. 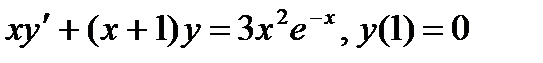 . 5. . 5. 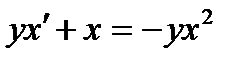 . 6. . 6.  7. 7. 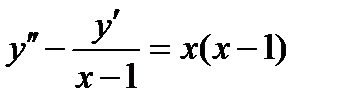 . 8. . 8. 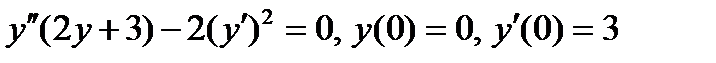 . 9. а) . 9. а)  ; б) ; б) 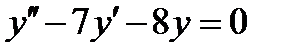 ; в) ; в) 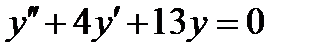 . 10. . 10. 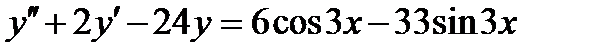 . 11. . 11.  . 12. . 12.  , ,  . . |
ВАРИАНТ 19 1. 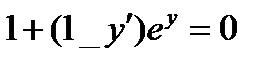 . 2. . 2. 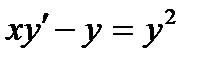 . 3. . 3.  . 4. . 4.  . 5. . 5.  . 6. . 6. 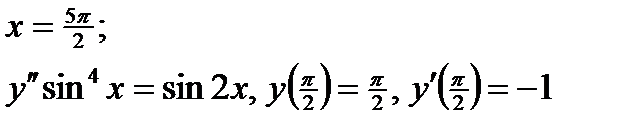 7. 7. 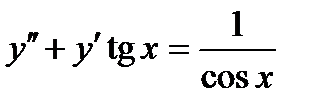 . 8. . 8. 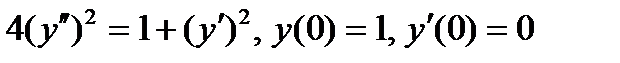 . 9. а) . 9. а)  ; б) ; б) 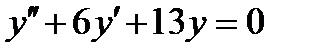 ; в) ; в)  . 10. . 10. 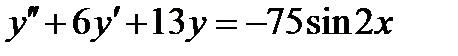 . 11. . 11.  . 12. . 12. 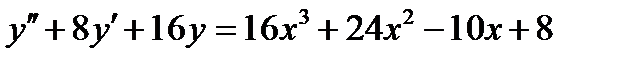 , , 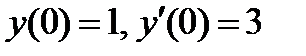 . . | ВАРИАНТ 20 1.  . 2. . 2. 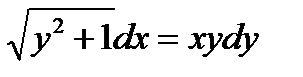 . 3. . 3. 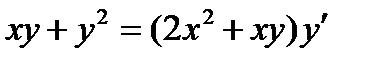 . 4. . 4.  . 5. . 5. 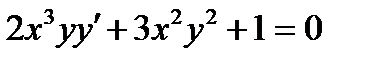 . 6. . 6. 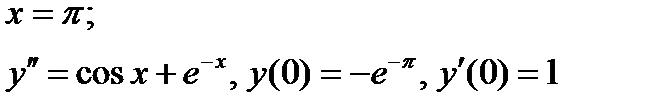 7. 7.  . 8. . 8. 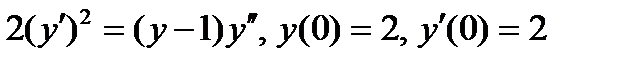 . 9. а) . 9. а)  ; б) ; б)  ; в) ; в)  . 10. . 10. 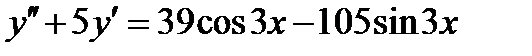 . 11. . 11.  . 12. . 12. 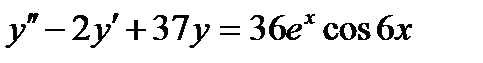 , ,  . . |
ВАРИАНТ 21 1.  . 2. . 2.  . 3. . 3. 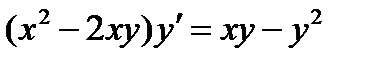 . 4. . 4.  . 5. . 5. 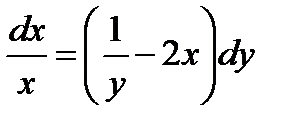 . 6. . 6. 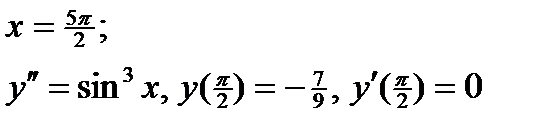 . 7. . 7. 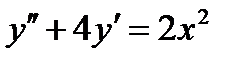 . 8. . 8.  . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 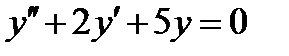 . 10. . 10.  . 11. . 11. 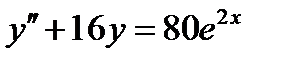 . 12. . 12.  , , 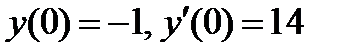 | ВАРИАНТ 22 1.  . 2. . 2.  . 3. . 3. 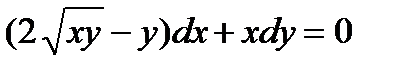 . 4. . 4.  . 5. . 5. 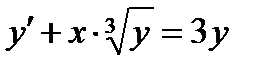 . 6. . 6. 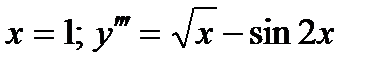 , , 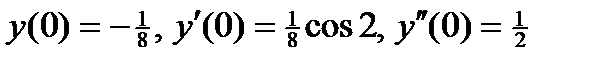 7. 7. 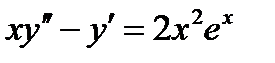 . 8. . 8. 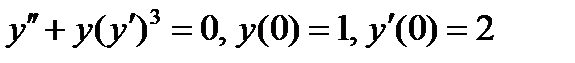 . 9. а) . 9. а) 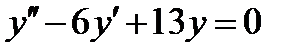 ; б) ; б) 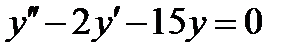 ; в) ; в)  . 10. . 10.  . 11. . 11. 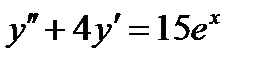 . 12. . 12. 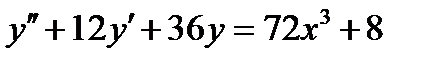 , , 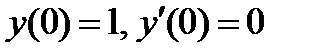 . . |
ВАРИАНТ 23 1. 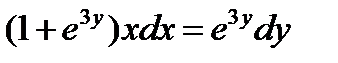 . 2. . 2. 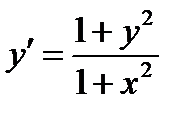 . 3. . 3.  . 4. . 4.  . 5. . 5.  . 6. . 6. 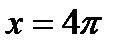 ; ;  . 7. . 7. 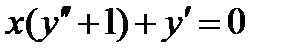 . 8. . 8. 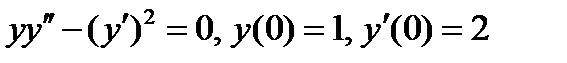 . 9. а) . 9. а) 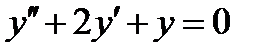 ; б) ; б) 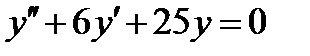 ; в) ; в) 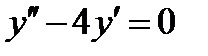 . 10. . 10. 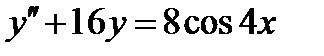 . 11. . 11. 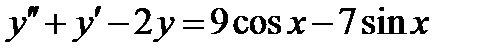 . 12. . 12.  , ,  . . | ВАРИАНТ 24 1. 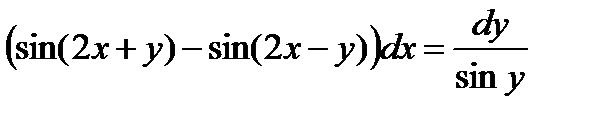 . 2. . 2. 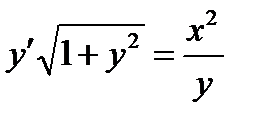 . 3. . 3. 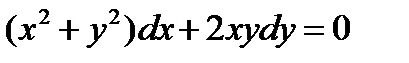 . 4. . 4. 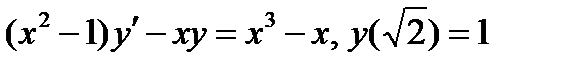 . 5. . 5.  . 6. . 6.  7. 7.  . 8. . 8. 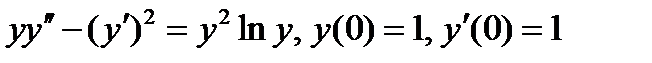 . 9. а) . 9. а) 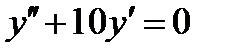 ; б) ; б) 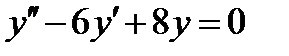 ; в) ; в) 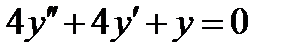 . 10. . 10.  . 11. . 11. 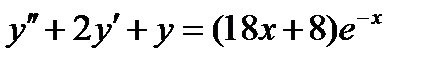 . 12. . 12. 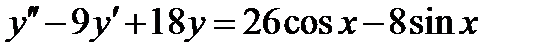 , , 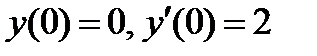 . . |
ВАРИАНТ 25 1.  . 2. . 2.  . 3. . 3.  . 4. . 4. 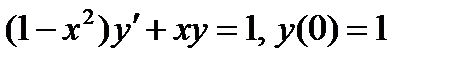 . 5. . 5. 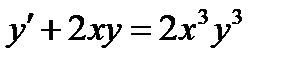 . 6. . 6.  7. 7. 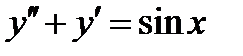 . 8. . 8. 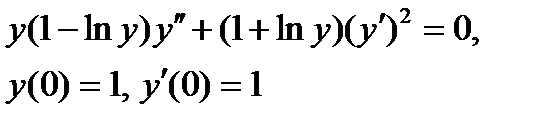 9. а) 9. а)  ; б) ; б) 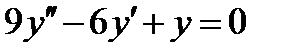 ; в) ; в) 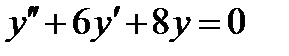 . 10. . 10. 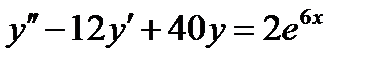 . 11. . 11. 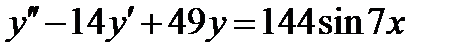 . 12. . 12. 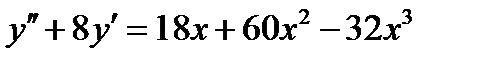 , , 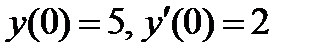 . . | ВАРИАНТ 26 1.  . 2. . 2. 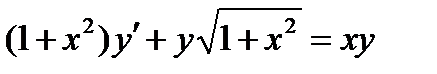 . 3. . 3.  . 4. . 4. 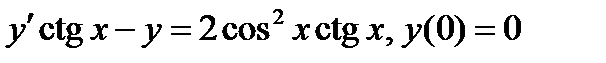 . 5. . 5. 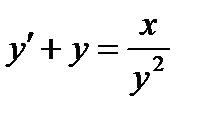 . 6. . 6. 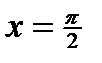 ; ;  . 7. . 7.  . 8. . 8. 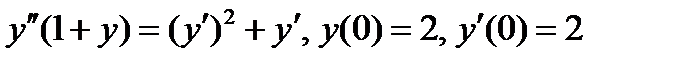 . 9. а) . 9. а) 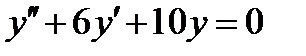 ; б) ; б) 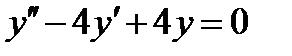 ; в) ; в)  . 10. . 10. 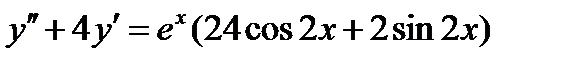 . 11. . 11. 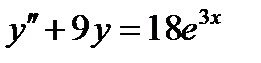 . 12. . 12.  , ,  . . |
ВАРИАНТ 27 1. 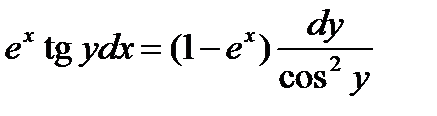 . 2. . 2.  . 3. . 3. 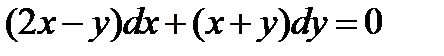 . 4. . 4.  . 5. . 5. 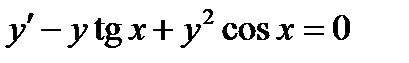 . 6. . 6. 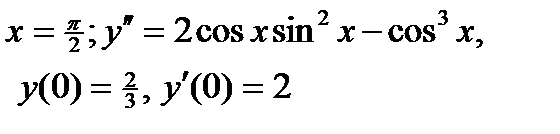 7. 7.  . 8. . 8.  . 9. а) . 9. а) 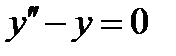 ; б) ; б) 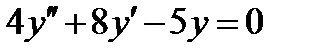 ; в) ; в) 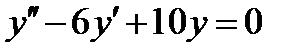 . 10. . 10.  . 11. . 11.  . 12. . 12.  , , 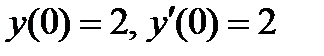 . . | ВАРИАНТ 28 1. 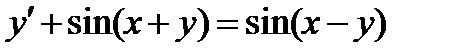 . 2. . 2. 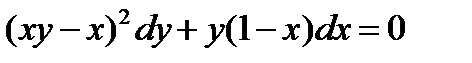 . 3. . 3. 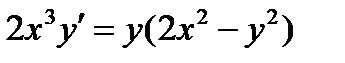 . 4. . 4.  . 5. . 5. 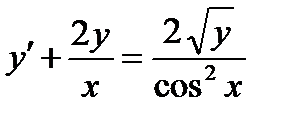 . 6. . 6. 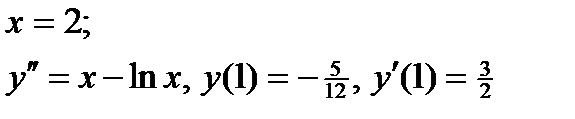 7. 7.  . 8. . 8.  . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 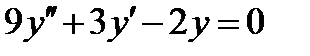 . 10. . 10. 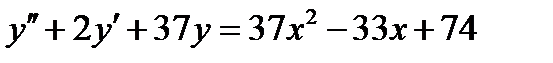 . 11. . 11.  . 12. . 12. 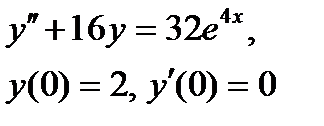 . . |
ВАРИАНТ 29 1.  . 2. . 2.  . 3. . 3. 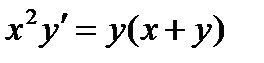 . 4. . 4. 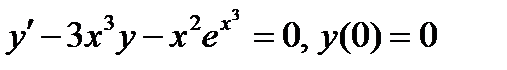 . 5. . 5.  . 6. . 6.  . 7. . 7. 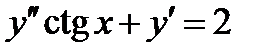 . 8. . 8.  . 9. а) . 9. а) 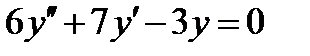 ; б) ; б) 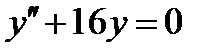 ; в) ; в)  . 10. . 10. 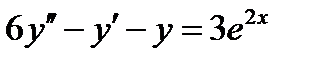 . 11. . 11. 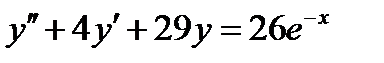 . 12. . 12. 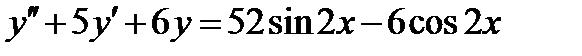 , , 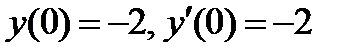 . . | ВАРИАНТ 30 1. 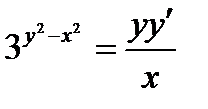 . 2. . 2. 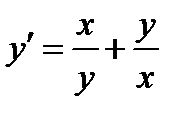 . 3. . 3. 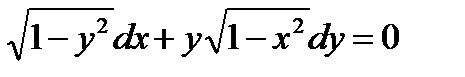 . 4. . 4. 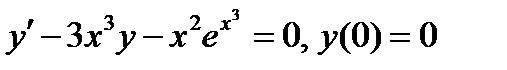 . 5. . 5. 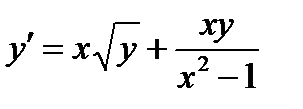 . 6. . 6.  7. 7. 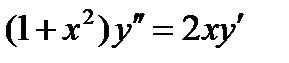 . 8. . 8.  . 9. а) . 9. а)  ; б) ; б)  ; в) ; в) 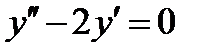 . 10. . 10. 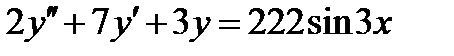 . 11. . 11. 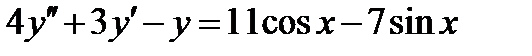 . 12. . 12.  . . |
Решение задач 1-5 типового варианта
Найти общее решение (общий интеграл) дифференциального уравнения.
1.  .
.
▲ Здесь  можно записать как (разложив на множители оба выражения):
можно записать как (разложив на множители оба выражения): 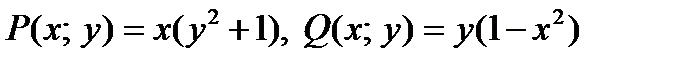 , где каждый из сомножителей зависит только от одной переменной. Следовательно, данное уравнение является уравнением с разделяющимися переменными (тип I).
, где каждый из сомножителей зависит только от одной переменной. Следовательно, данное уравнение является уравнением с разделяющимися переменными (тип I).

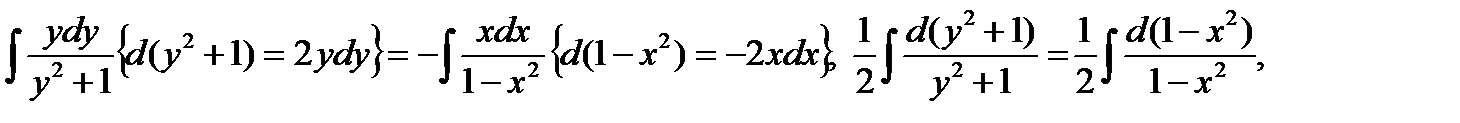
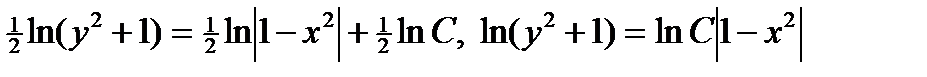 .
.
Следовательно, общим интегралом исходного уравнения является 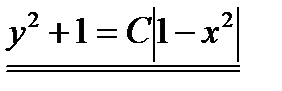 . ▼
. ▼
2.  .
.
▲ Здесь функции  представляют собой выражения, в которых каждый из сомножителей зависит только от одной переменной. Поэтому исходное уравнение является уравнением типа I.
представляют собой выражения, в которых каждый из сомножителей зависит только от одной переменной. Поэтому исходное уравнение является уравнением типа I.
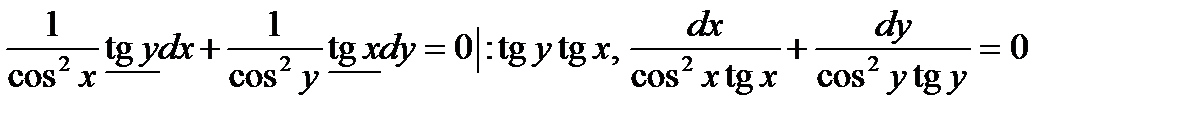 .
.
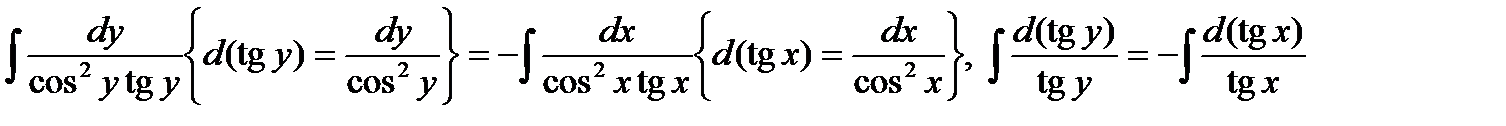 ,
,
 .
.
 − общий интеграл дифференциального уравнения. ▼
− общий интеграл дифференциального уравнения. ▼
3. 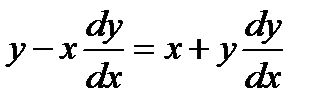 .
.
▲ Запишем уравнение в нормальной форме  .
.
 .
.
Следовательно, 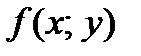 − однородная функция нулевого измерения, потому исходное уравнение однородное.
− однородная функция нулевого измерения, потому исходное уравнение однородное.
 ,
,
 .
.
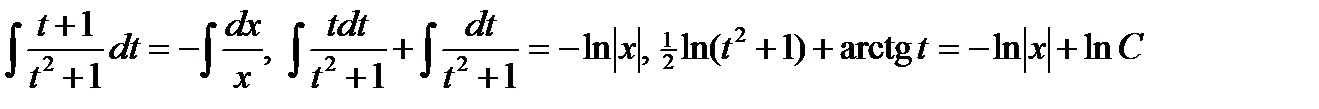 ,
,
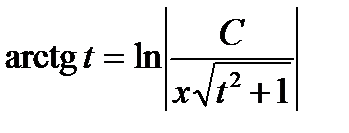 . Общий интеграл исходного уравнения:
. Общий интеграл исходного уравнения:  . ▼
. ▼
4. Найти частное решение дифференциального уравнения
 .
.
▲ Приведем подобные члены относительно 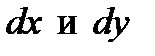 и преобразуем уравнение, выделив производную
и преобразуем уравнение, выделив производную
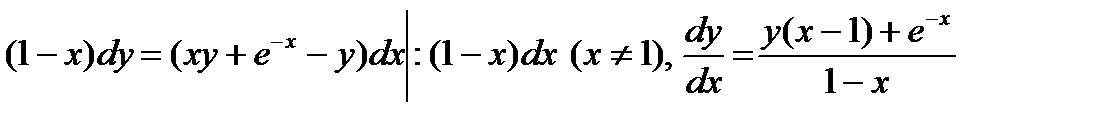 ,
, 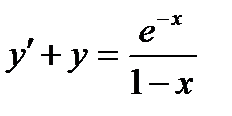 .
.
Функция, ее производная входят в уравнение в первой степени (линейно). Следовательно, данное уравнение линейное. Решаем его.