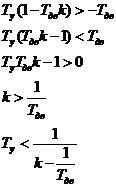В АС возможен астатизм, если в структуре разомкнутой АС имеются интегрирующие звенья.

Структурный признак астатизма по отношению к возмущающему воздействию:

В АС возможен астатизм по отношению к возмущающему воздействию F(t) , если в структуру разомкнутой АС входят интегрирующие звенья, расположенные до точки приложения возмущающего воздействия.

Синтез- задача построения такой структуры при которой она будет обладать необходимым нам качеством.

НЧ – отвечает за точность АС в статическом режиме.

СЧ – определяет запас устойчивости и основной показатель качества (время переходного процесса и процесса).

ВЧ – характеризует уровень помехозащищенность от ВЧ помех

Нелинейная автоматическая система.

АС назовем нелинейной если в ее структуру входит хотя бы 1 нелинейность.

Нелинейность – элементы АС которые имеют нелинейную статическую характеристику либо его динамика описывается нелинейным ДУ.

Типовые линейности АС.

Типовые нелинейности являются идеализированными зависимостями между входной и выходной величинами.

Кусочно линейная функция	Линейная функция с насыщением
Нелинейность типа «Идеальное Реле»	4. Линейность кусочная с насыщением и зоной
5. Идеальное реле с зоной нечувствительности(гистерезис запаздывает)	6. Идеальное реле с запаздыванием
7. Идеальное реле с запаздыванием и зоной нечувствительности	Замечания о методах исследования нелинейных АС.

Автоколебания– самовозбуждающиеся колебания самоустанавливающиеся и самоподдерживающиеся.

Назовем энергией подкачки за период ту энергию, которая поступает в систему от источника энергии за период.

Назовем энергию, которая возникла от потерь, от сил трения, излучения, энергией десипации, или ту энергию, которая теряет нелинейная система за период колебаний.

Фазовое пространство— пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.

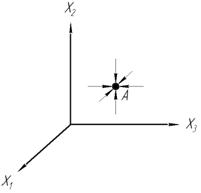Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.

Пусть все фазовые траектории стягиваются в точку

Точка А является положением равновесия, причем она устойчива.

Пусть в точку А, в которую входят все траектории можно назвать аттрактор.

Положением равновесия м.б. целой областью – аттрактором.

ЗАДАЧИ

1. Методика определения характеристического уравнения замкнутой АС!!!

Вспомним характеристическое уравнение Замкнутой АС

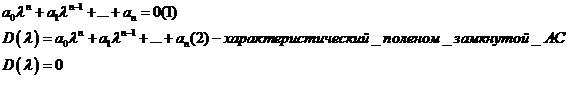
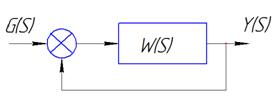Решим задачу определения характеристического поленома замкнутой АС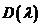

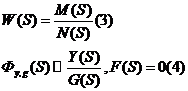
Правило 1:Определяем характеристический поленом замкнутой АС путем сложения знаменателя и числителя, как сумму числителя и знаменателя, с последующей заменой оператора АС(S) на лямбда.

N(S)+M(S)=D(S)|s=лямбда=Д(лямбда)

Правило 2: Определяем А(S)

А(S)|s=лямбда=Д(лямбда)

Правило 3:

Разрешается не заменять S на лямбда, условно считать что Sэто лямбда.

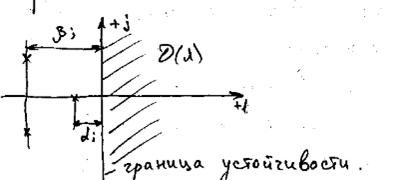Дляустойчивости замкнутой АС необходимо и достаточно чтобы корни характеристического уравнения лежали в левой полуплоскости на комплексной полуплоскости.

ПРИМЕР:

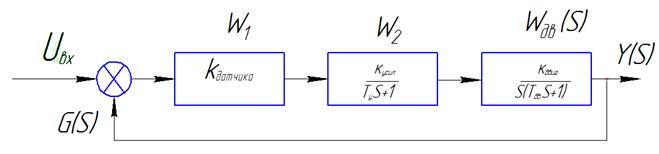
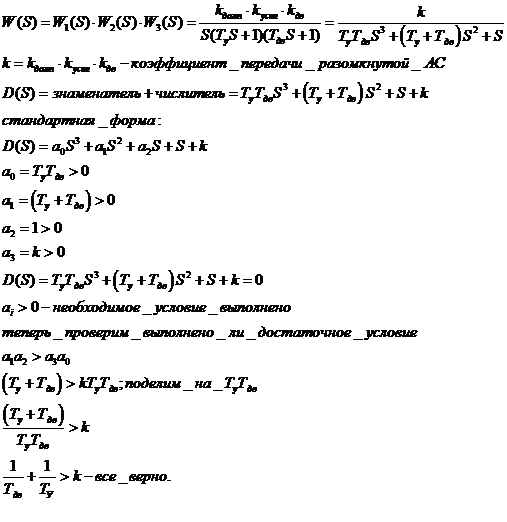
1. Алгебраический критерий Гурвица

Пример:

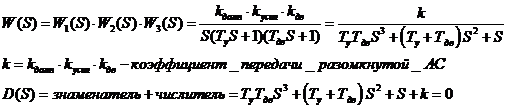
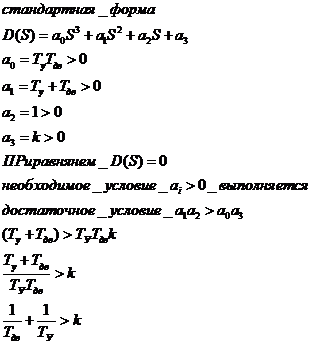
Ыыыыыы

2.2. По критерию Гурвица:

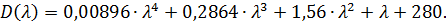
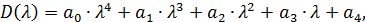
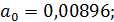
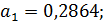
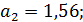
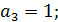
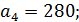
Поскольку 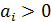, то необходимо найт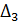и и .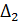

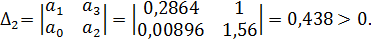
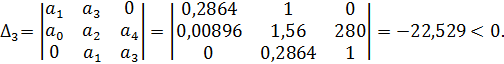
Поскольку 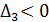, то критерий Гурвица не выполняется и система является неустойчивой.

1. Алгебраический критерий Михайлова

Пример:

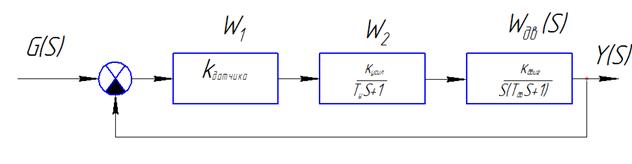
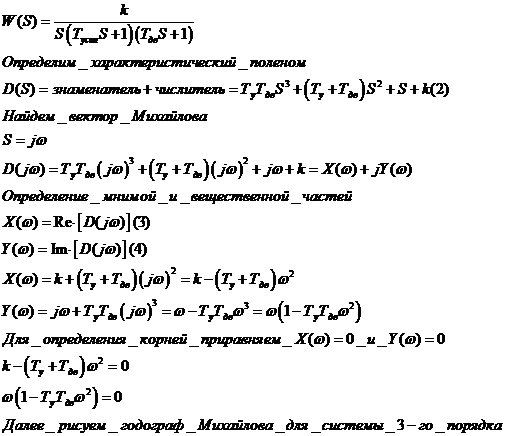
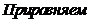
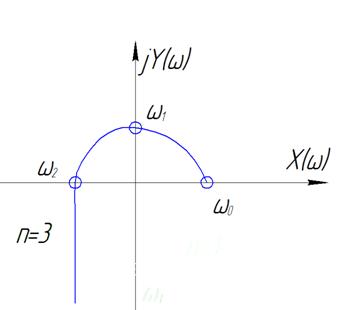
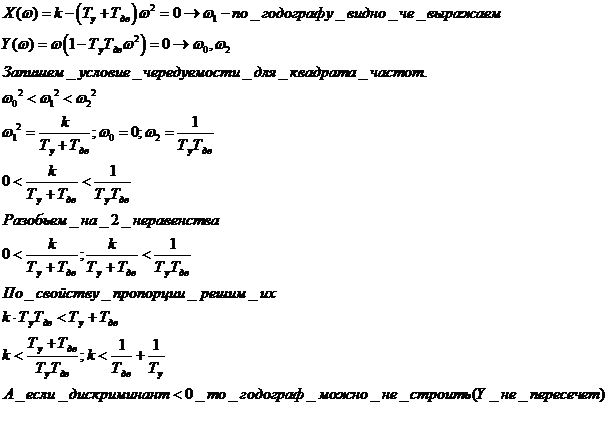
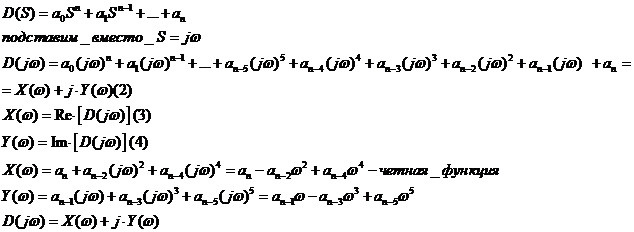
1. Построение области устойчивости

правило штриховки.

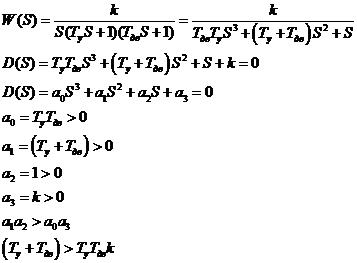
Неравенства превратим в равенство:

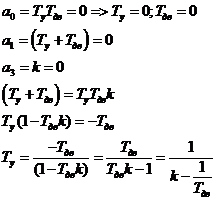
Используя необходимое условие и используя физический смысл коэффициента усиления к и Ту получим:

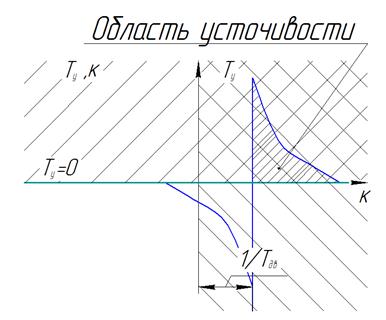
При определении области устойчивости используем правило штриховки.

Выразим