Общее уравнение динамики системы

При идеальных голономных удерживающих связях, наложенных на систему, имеет место общее уравнение динамики:

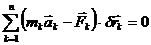(79)

или

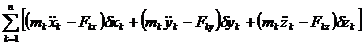(80)

уравнение (79) можно переписать в виде

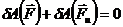(81)

т. е. при движении системы с идеальными голономными удерживающими связями сумма элементарных работ активных сил и сил инерции равна нулю на всяком воз­можном перемещении систе­мы из любого ее положения.

Работу сил инерции твер­дого тела, вращающегося во­круг неподвижной оси, при элементарном повороте δφ вокруг оси вращения опре­деляют формулой

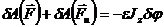, (82)

где J_z - момент инерции тела относительно оси враще-ния. В случае наличия сил трения их нужно причислять к активным силам.

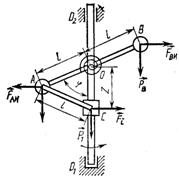Пример 1.(рис. 567). Центробежный тахометр со­стоит из двух точечных масс А и В, соединенных между собой стерж-нем, муфтыС, скрепленной с массой А с по­мощью стержня АС и спиральной пружины. Стержень АВ может поворачивать-ся вокруг оси О, перпендикуляр­ной оси тахометра O₁O₂. При отсутствии вращения стер­жень АВ образует с осью тахометра угол φ₀. Опреде­лить зависимость угловой скорости тахометра от угла φ, если масса т_А = т_В = т, а масса муфты равна m₁. Жест­кость спиральной пружины принять равной с и считать

ОА = OВ = АС = l. Массой стержней и трением пренебречь.

Решение. Система состоит из точечных масс A и В и муф-ты С. Активными силами являются веса и упругие силы

пружины, момент последних M_упр = C(φ – φ₀). Приложим условно к точкам системы силы инерции:

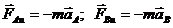
Pис. 567 Так как 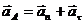, а 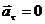в силу равномерности вращения, то 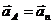, т. е.

a_A = ω²l sin φ.

Таким образом,

F_Aи = F_Ви = mω²l sin φ.

При этом силы инерции являются центробежными и направлены перпендикулярно оси вращения.

Если не пренебрегать размерами муфты, то к каждой частице муфты будет приложена сила инерции 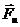, также являющаяся центро­бежной. Приложив силы инерции, сооб-щим системе возможное пере­мещение δφ, повернув мысленно стержень АВ вокруг точки О в плоскости рисунка. Определим элементарную работу задаваемых сил и сил инерции.

При повороте твердого тела 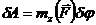. Обозначая Р_А = Р_В = P = тg - веса грузов, получим:

; ;

; .

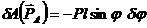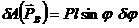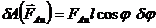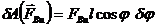Работа упругих сил /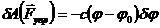

Работу веса 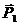муфты С найдемпо формуле

,

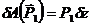где δz - изменение расстояния муфты от точки О.

Так как z = l cos φ, то 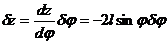и, следовательно, .

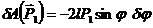Работа сил инерции 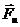на возможном перемещении равна

нулю, так как эти силы перпендикулярны элементарным пере-мещениям. Таким образом, согласно (81)

.

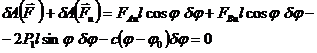Подставив найденные значения, получим

,

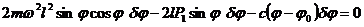отсюда

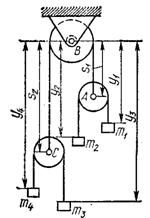
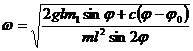
Пример 2. Система состоит из четырех масс m₁, m₂, т₃, т₄, соеди-ненных попарно и подвешенных с помощью блоков А, В, С (рис. 568). Определить, при каком соотношении масс груз с массой т₄ будет оста-ваться на месте, если в начальный момент система на­ходилась в покое. Массой блоков, ни­тей и трением пренебречь.

Решение. Система имеет три степени сво­боды. Обозначим абсо-лютные координаты гру­зов через y₁,

Рис.568 у₂, у₃, у₄. Активными силами

являются веса. Согласно уравнению (80)

.

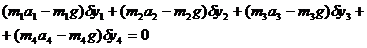Установим зависимость между перемещениями δy₁, δу₂, δу₃, δу₄. для чего составим уравнения связей. Так как все нити предполага­ются нерастяжимыми, то, обозначая через L₁, L₂, L₃ длины нитей, получим

y₁-s₁+ у₂ - s₁ + πr_A= L₁; s₁+ s₂ + π_B = L₂; у₃ - s₂ + у₄ - s₂ + πr_C = L₃.

Умножая второе уравнение на 2 и складывая все три уравнения (чтобы исключить s₁ и s₂), получим

y₁ + у₂ + у₃ + у₄ = 2L₂ - 2πr_B + L₁ + πr_A+ L₃ - πr_C = const.

(поскольку система имеет три степени свободы, это единст-венное уравнение связи). Варьируя, найдем δy₁+δу₂+δу₃+δу₄= 0, а дважды дифференцируя по времени, получим

a_l +a₂ +a₃ +a₄ = 0.

Заменяя δy₄ его выражением через δy₁, δу₂, δу₃,получим

[m₁(a₁ - g) - m₄(a₄ - g)]δy₁ + [m₂(a₂ - g) - m₄(a₄ - g)] δу₂ +

+[m₃(a₃ - g) - m₄(a₄ - g)] δу₃ = 0.

Так как вариации δy₁, δу₂, δу₃ взаимно независимы, то коэффи­циенты при них должны быть равны пулю, отсюда

m₁(a₁ - g) = m₄(a₄ - g);

m₂(a₂ - g) = m₄(a₄ - g);

m₃(a₃ - g) = m₄(a₄ - g).

Умножая эти равенства соответственно на т₂т₃, т₁m₃, т₁т₂ и складывая, получим

.

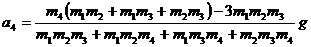Для того чтобы груз массой т₄ при отсутствии начальной ско­рости не двигался, необходимо, чтобы a₄ = 0, т. е.

.

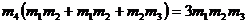Разделив обе части этого соотношения на т₁т₂т₃, можем пред­ставить его в виде

.

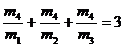Это и есть искомая зависимость между массами грузов.

Задачи

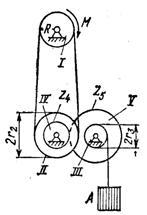
3.9.1*. К ведущему барабану I радиусом R подъемного механизма приложен постоянный вращающий момент М (рис. 528). Oпреде­лить модуль ускорения поднимае­мого груза А, если радиусы барабанов//

Рис. 569 и III соответственно равны r₂ и r₃, передаточное чи­сло z₅/z₄ = u, а масса груза рав­на т,не учитывая масс вращаю­щихся частей и тросов и пренеб-регая трением в осях.

Ответ: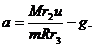

3.9.2*. Решить предыдущую задачу с учетом масс вращающихся частей механизма, приняв моменты инер­ции: ведущего барабана – J₁, барабана II с зубчатым колесом – J₂ барабана III с зубчатым колесом – J₃.

Ответ: .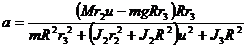

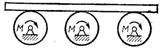3.9.3*. На трех сплошных однородных валах (рис. 570), к каждому из которых приложен вращающий мо­мент М, находится балка массой т_2. Определить мо-дуль ускоре­ния балки, если масса каждого вала равна т₁, а радиус равен r, считая, что между валами и балкой сколь-жение отсутствует. Трением в

Рис. 570 осях пренебречь.

Ответ: .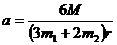

Определение обобщенных сил инерции в системах с одной и двумя степенями свободы

3.9.4. Могут ли элементарные работы сил инерции в общем уравнении динамики, составленном для механической системы с одной степенью свободы, иметь разные знаки? (Нет)

3.9.5.Определить обобщенную силу инерции, соответствующую обобщенной координате х₂ (рис. 571), если сила инерции тела 1 Ф = 5 Н, переносная и относи-тельная силы инерции тела 2 соответ­ственно 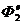= 1 Н, 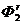= 8 Н. (-7,29)

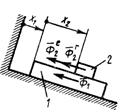
3.9.6.Определить обобщенную силу инерции, соот-ветствующую обобщенной координате х₁ (рис. 672), если сила инерции тела 1 Ф₁ = 5 Н, переносная и тносительная силы инерции тела 2 соответ­ственно 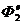= 1 Н, 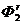= 8 Н. (-0,344)

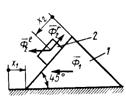
3.9.7. Определить обобщенную силу инерции, соответствующую обобщенной координате х₂ (рис. 573 ), если сила инерции тела 1 Ф₁= 8 Н, переносная и относи-тельная силы инерции тела 2 соответ­ственно 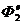= 5 Н, 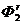= 5 Н. (-10)

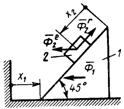
Рис. 571 Рис. 572 Рис. 573

3.9.8. Определить обобщенную силу инерции, соот-ветствующую обобщенной координате х₁ (рис. 574),если сила инерции тела 2 Ф₁ = 4 Н, переносная и относитель-ная силы инерции тела 2 соответ­ственно 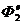=2 Н, 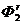=1 Н, переносная и отно­сительная силы инерции тела 3

соответственно 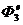= 2 Н, 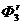= 1 Н (-9)

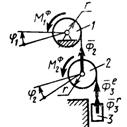
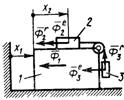
Рис. 574 Рис. 575

3.9.10. Определить обобщенную силу инерции, соответствующую обобщенной координате φ₁ (рис. 575), если сила инерции тела 2 Ф₂ = 0,4 Н, перенос­ная и отно-сительная силы инерции тела 3 соот­ветственно 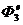= 0,2Н 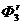= 0,1 Н, моменты сил инерции 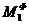= 0,4 Н м, 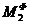= 0,1 Н·м, радиус r = 0,2 м (-0,54)