Критерий Коши сходимости ряда.

Числовые ряды.

Определение 1.

Пусть

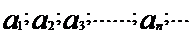
бесконечная последовательность чисел, которые могут быть как вещественными, так и комплексными. Выражение

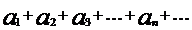
называется числовым рядом.

Иногда для обозначения ряда применяют следующую запись:

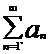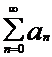или , в зависимости от того, с какого элемента удобно начинать нумерацию.

Обычно элемент ряда 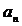описывается как некоторая функция своего номера. Аналитическое выражение этой функции часто называют «общим» членом (элементом) ряда.

Например, гармонический ряд

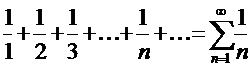имеет «общий» член .

Определение 2.

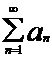
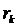Ряд , членами которого являются все члены ряда , начиная с (k+1)- го, взятые в том же порядке, что и в исходном ряде, называется остатком k-го порядка ряда , и обозначается , то есть

.

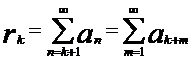Определение 3.

Сумма k первых членов ряда 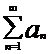называется k-ой частичной суммой или частичной суммой порядка k и обозначается 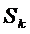, то есть

.

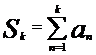Очевидно, первая, вторая, третья и т. д. частичные суммы ряда

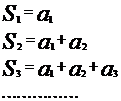
составляют бесконечную последовательность 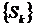. Таким образом, каждому ряду соответствует последовательность его частичных сумм.

Определение 4.

Ряд 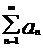называется сходящимся, если сходится (имеет предел) последовательность 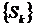его частичных сумм.

Ряд 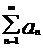называется расходящимся, если последовательность 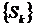его частичных сумм расходится.

Если ряд 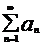сходится, то число 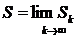называется его суммой, при этом пишут .

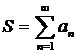Если ряд расходится, то 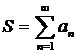и его остаток 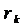любого порядка расходится. Если ряд сходится, то и его остаток k-ого порядка 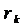при любом k сходится, в этом случае , .

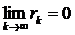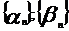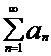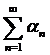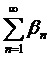Если члены ряда - комплексные числа , где - действительные последовательности , то сходимость ряда эквивалентна одновременной сходимости рядов и и

.

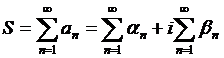Таким образом, исследование свойств рядов с комплексными членами сводится к исследованию рядов с действительными членами.

Пример 1.Рассмотрим ряд

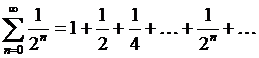
Частичная сумма 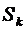этого ряда есть

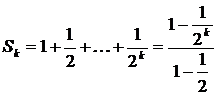
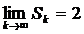. Следовательно, данный ряд сходится, и его сумма равна 2.

Пример 2.

Рассмотрим ряд

Поскольку для этого ряда 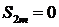, для любого натурального m, то последовательность 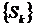не имеет предела. Следовательно, данный ряд расходится.

В большинстве случаев, непосредственный анализ последовательности 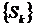не представляется возможным, поэтому основными задачами в теории числовых рядов являются установление сходимости или расходимости данного ряда без вычисления величины его суммы и оценка зависимости остатка ряда 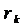от номера k (скорость сходимости ряда).

В силу равенства , оценка 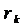даёт оценку погрешности при замене суммы ряда S частичной суммой .

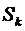Пример 3.

Пользуясь критерием Коши, покажем, что гармонический ряд 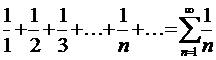расходится. Для этого надо указать такое число 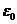>0, что для любого номера N и некоторой пары натуральных чисел p и n, n>N , имеет место неравенство .

Возьмём произвольное натуральное число n .Тогда

.

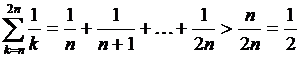Таким образом, для 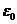=1/2 и произвольного номера N найдены натуральные числа n=N+1 и p=n ,для которых 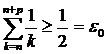, что и требовалось установить. Следовательно, гармонический ряд расходится.

Пример 4.

Ряд 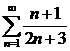расходится по необходимому признаку, так как .

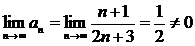Первый признак сравнения.

Пусть два ряда 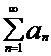и 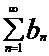таковы, что члены первого, начиная с некоторого номера, не превосходят соответствующих членов второго:

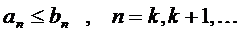
Тогда из сходимости ряда 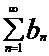следует сходимость ряда 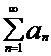, а из расходимости ряда 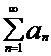следует расходимость ряда .

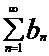Пример 5.

Рассмотрим ряд 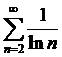. Сравним его с уже известным нам расходящимся гармоническим рядом .

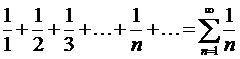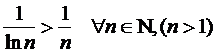. Значит, и наш ряд расходится по признаку

сравнения.

Пример 6 .

Рассмотрим ряд 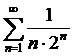. Для выяснения вопроса о его сходимости сравним его с рядом - это рассмотренная нами выше сумма геометрической прогрессии (см. Пример 1).

В данном случае все члены нашего ряда не превосходят членов сходящегося ряда, и множитель n в знаменателе только «усиливает» сходимость: .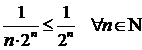

Также необходимо помнить, что ничего нельзя сказать о сходимости ряда, все члены которого не превосходят членов расходящегося ряда, так и о сходимости ряда, все члены которого превосходят члены сходящегося ряда.

Например, члены рядов 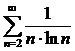и 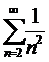меньше членов расходящегося гармонического ряда , однако ряд 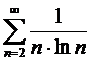является расходящимся, а ряд 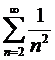- сходящимся!

Второй признак сравнения.

Если даны два ряда 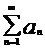и 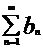, и выполняется соотношение

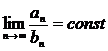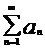, то и 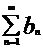сходятся или расходятся одновременно.

Пример 7.

Ряд 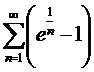«ведёт себя» подобно гармоническому ряду а именно, расходится, так как .

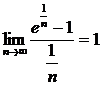В качестве рядов, используемых для сравнения, чаще всего применяются ряды вида 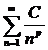(их называют рядами Дирихле) и , где С – постоянная или ограниченная величина.

Изучить их поведение попробуем с помощью

Пример 8.

Рассмотрим поведение рядов Дирихле 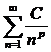в зависимости от p.

Для них f(x)= 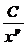. В этом случае

Для случая p=1 f(x)=1/x

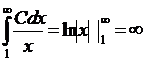- интеграл расходится, что ещё раз доказывает расходимость гармонического ряда.

Итак, ряды вида 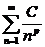сходятся при p>1 и расходятся при p<1 и при p=1.

Пример 9.

В данном случае можно применить признак сравнения с рядом Дирихле после преобразования общего члена ряда с помощью формул Тейлора. Напомним их:

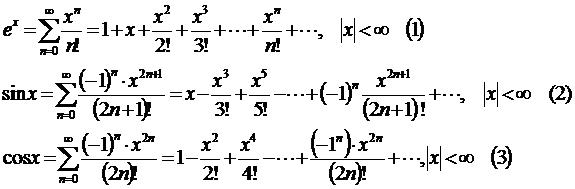
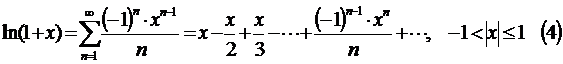
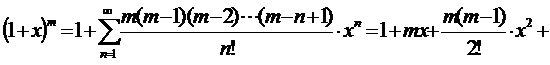
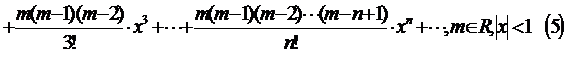
С помощью формулы (5) получим:

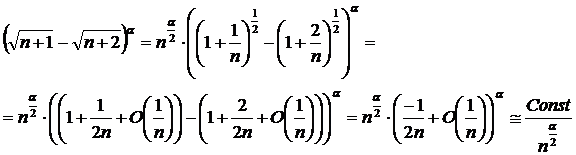
С помощью формулы (4) можем получить:

Тогда

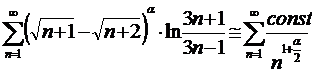
Имеем ряд Дирихле 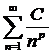, где p=1+ 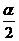. Такой ряд сходится при p>1, то есть при 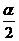>0, и расходится при p≤1, то есть при 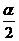≤0.

Пример 10.Ряд .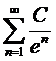

Применим интегральный признак: f(x)= 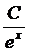, несобственный интеграл 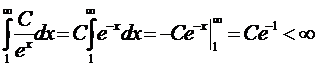сходится. Следовательно, сходится и ряд .

Пример 11.Ряд .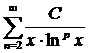

Случай p=1. f(x)= 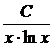. Применяем интегральный признак: 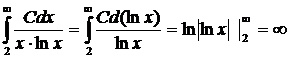- несобственный интеграл, а, вместе с ним и ряд расходятся.

Случай p≠1:

.

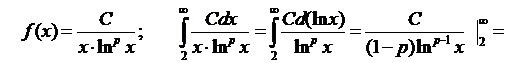
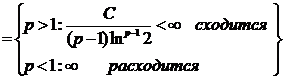Вместе с соответствующим несобственным интегралом, в зависимости от p, ряд 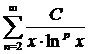сходится при p>1 и расходится при p≤1.

Необходимо отметить ещё один момент: множество сходящихся рядов образуют линейное пространство. Этим тоже можно пользоваться для установления сходимости рядов. А именно: если исследуемый ряд может быть представлен в виде конечной линейной комбинации сходящихся рядов, то он сходится.

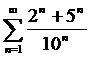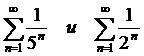Пример 12. . Так как и каждый из рядов сходятся (см. пример 1), то и ряд 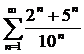сходится.

Если исходный ряд может быть представлен в виде линейной комбинации сходящегося и расходящегося рядов, то он расходится.

Пример 13.

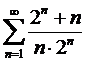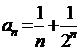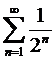Рассмотрим ряд . Так как , ряд сходится, а ряд 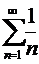расходится, то ряд 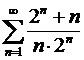расходится.

Множество всех расходящихся рядов не образуют линейное пространство! Поэтому их конечные линейные комбинации могут образовывать как сходящийся, так и расходящийся ряд.

Пример 14.

Рассмотрим ряд .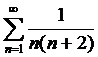

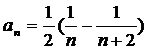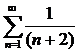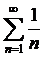. Ряды и расходятся, однако исходный ряд сходится!

Докажем это двумя способами:

Во-первых (по признаку сравнения), 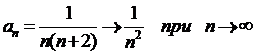, следовательно, наш ряд сходится вместе с рядом Дирихле 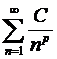, С=1, p=2.

Во-вторых, попробуем получить частичную сумму данного ряда, чтобы доказать сходимость по определению – через предел частичных сумм. Так как 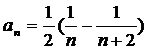, то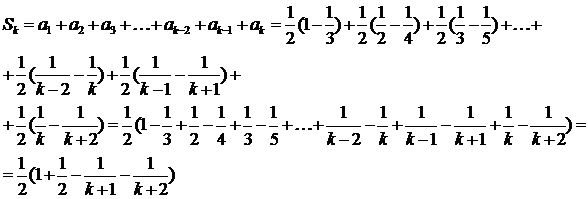

. Предел частичной суммы существует, конечен, следовательно, ряд 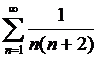сходится по определению.

Признак Даламбера.

Пусть дан ряд с положительными членами 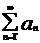, , 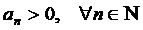тогда, если 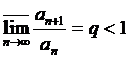, то ряд сходится,

если 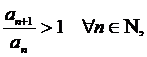и в частности, если 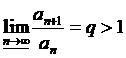, то ряд расходится.

Если q=1, необходимо применить другой признак, так как при q=1 признак Даламбера не даёт ответа на вопрос о сходимости ряда.

Признак Даламбера удобнее всех прочих применять в том случае, если в выражении 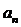члена ряда содержится знак факториала.

Пример 15. .

По признаку Даламбера:

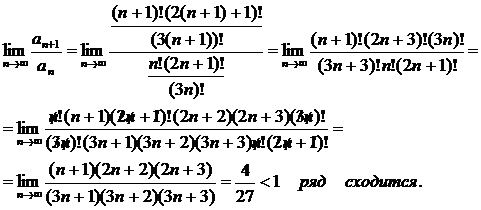
Пример 16.

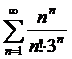
По признаку Даламбера:

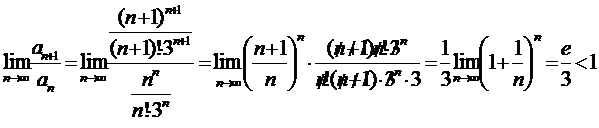- ряд сходится.

Отметим, что полученное соотношение 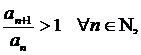указывает на невыполнение необходимого признака сходимости ряда

.

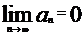Признак Коши (радикальный).

Пусть дан ряд с неотрицательными членами: , .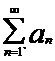

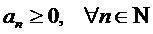Тогда если 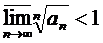, то ряд сходится,

если 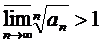, то ряд расходится.

Если же 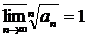, то признак Коши не является информативным для данного случая, необходимо применить другой признак.

Пример 17.

.

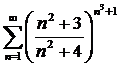Применим признак Коши: 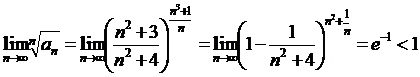ряд сходится.

Пример 18.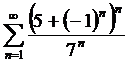

В зависимости от чётности n при 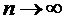последовательность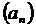

будет иметь два частичных предела. Поэтому: ,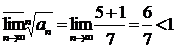

ряд сходится.

Пример 19.

.

Для начала применим признак Даламбера.

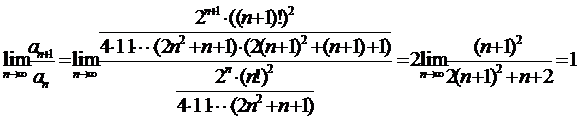
Как видно, этот признак не работает. В таких случаях следует применять

Признак Гаусса.

Если 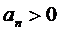и существует такое число ε>0, такое что

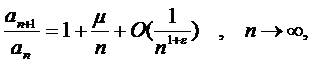
то ряд 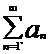сходится, если μ<-1 , и расходится, если μ≥-1.

Продолжим рассмотрение примера 18.Применим признак Гаусса:

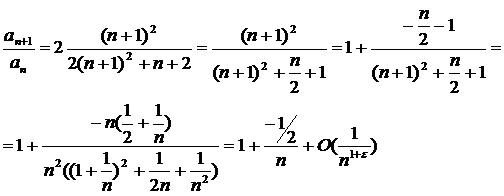
Как видно, μ=-1/2>-1 - следовательно, ряд расходится.

Для закрепления приведем ещё примеры:

Пример 20.

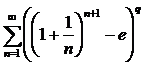.Преобразуем общий член ряда с помощью формул Тейлора, чтобы применить признак сравнения. Также нам понадобится формула .

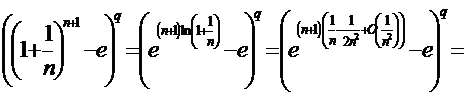
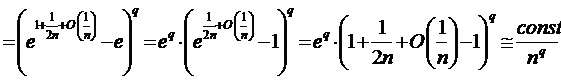
Получили для сравнения ряд Дирихле 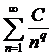, который сходится при q>1 и расходится при q≤1.

Пример 21.

.

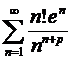Применим признак Даламбера:

.

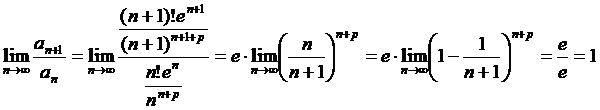Признак Даламбера не информативен – применим признак Гаусса:

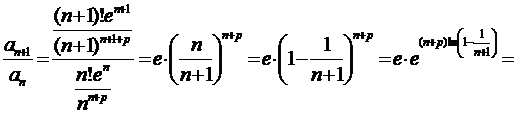
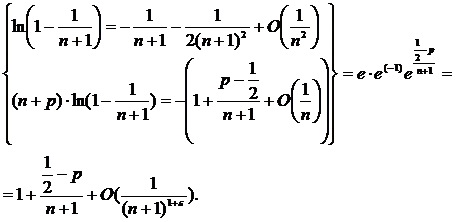
Таким образом, μ=1/2-p, то есть, данный ряд сходится при р>3/2 и расходится при p≤3/2.

При решении данного примера были использованы стандартные разложения Тейлора в степенной ряд для функций ln(1+x) и 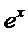,а также известная из школьного курса формула

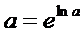была применена для преобразования вида

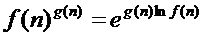.(В нашем случае ).

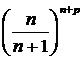Пример 22.

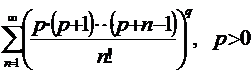
Признак Даламбера не даёт информации о сходимости ряда:

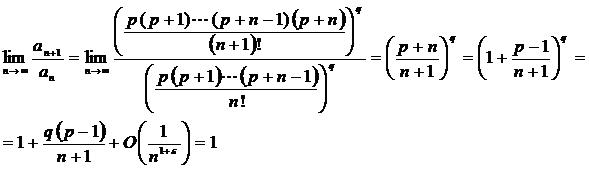
Применим признак Гаусса: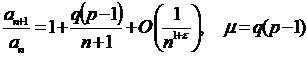

Следовательно, ряд сходится ,если 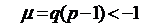и расходится, если .

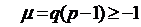Признак Абеля.

Пусть дан ряд 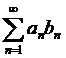. Если последовательность 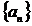монотонна и ограничена, а ряд 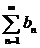сходится, то ряд 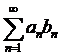сходится.

Признак Дирихле.

Пусть дан ряд 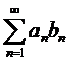. Если последовательность 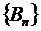, 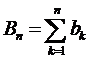ограничена, а последовательность 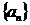монотонно стремится к нулю, то ряд 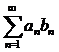сходится.

Определение.Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют различные знаки, то есть ряд вида .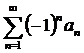

Признак Лейбница (для знакочередующихся рядов).

Если последовательность 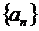положительных чисел монотонно стремится к нулю, то ряд 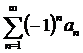сходится и его остаток 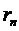удовлетворяет неравенству .

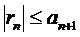Обратим внимание на то, что в признаке сходимости Лейбница указываются триусловия, которым должен удовлетворять ряд: знакочередуемость членов ряда, а также монотонность и сходимость к нулю их абсолютных величин. Убедимся в том, что каждое из этих трёх условий является существенным.

Пример 23.

В ряде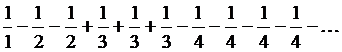

Абсолютные величины членов не возрастают и стремятся к нулю, однако, все частичные суммы вида

,

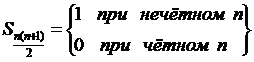а остальные принимают промежуточные значения. Очевидно, такая последовательность частичных сумм предела не имеет, и потому ряд расходится.

Пример 24.

Ряд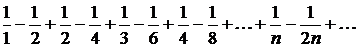

знакочередующийся, но нет монотонного стремления членов ряда к нулю. Этот ряд расходится. В самом деле, если бы он сходился, то в том числе и по ассоциативному закону:

Если в сходящемся ряде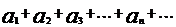

произвольно объединить соседние члены в группы, не нарушая порядка членов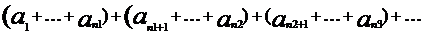

то составленный из этих групп ряд будет сходиться и иметь ту же сумму, что и первоначальный ряд.

Но ряд

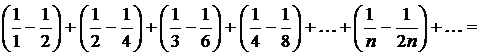
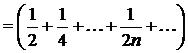
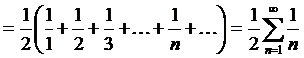
является гармоническим, который, как известно, расходится.

Наконец, невыполнение третьего условия признака Лейбница - стремления к нулю абсолютного значения члена ряда при n→∞ - это нарушение необходимого признака сходимости ряда.

В заключение приведём несколько примеров:

Пример 25.

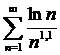
Данный ряд не является знакопеременным, но для исследования его на сходимость хорошо подходит признак Абеля.

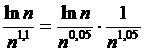
Последовательность 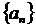= 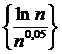является ограниченной и монотонной,

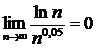,что доказывают по правилу Лопиталя (0,05>0), ряд 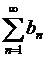=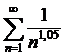сходится, как ряд Дирихле для p=1,05>1. Следовательно, ряд 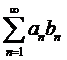=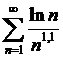сходится.

Пример 26.

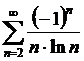
Данный ряд - знакочередующийся, или ряд Лейбница. Начинаем с исследования на абсолютную сходимость:

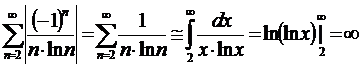ряд из модулей расходится по интегральному признаку - абсолютной сходимости нет.

Применим признак Лейбница:

Последовательность 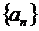= 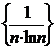монотонно стремится к нулю, следовательно, ряд 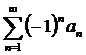=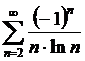сходится условно.

Числовые ряды.

Определение 1.

Пусть

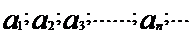
бесконечная последовательность чисел, которые могут быть как вещественными, так и комплексными. Выражение

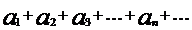
называется числовым рядом.

Иногда для обозначения ряда применяют следующую запись:

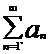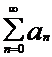или , в зависимости от того, с какого элемента удобно начинать нумерацию.

Обычно элемент ряда 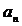описывается как некоторая функция своего номера. Аналитическое выражение этой функции часто называют «общим» членом (элементом) ряда.

Например, гармонический ряд

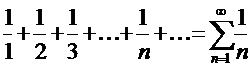имеет «общий» член .

Определение 2.

Ряд , членами которого являются все члены ряда 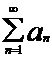, начиная с (k+1)- го, взятые в том же порядке, что и в исходном ряде, называется остатком k-го порядка ряда 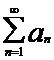, и обозначается 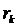, то есть

.

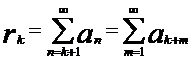Определение 3.

Сумма k первых членов ряда 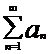называется k-ой частичной суммой или частичной суммой порядка k и обозначается 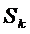, то есть

.

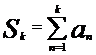Очевидно, первая, вторая, третья и т. д. частичные суммы ряда

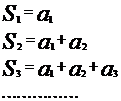
составляют бесконечную последовательность 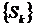. Таким образом, каждому ряду соответствует последовательность его частичных сумм.

Определение 4.

Ряд 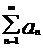называется сходящимся, если сходится (имеет предел) последовательность 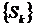его частичных сумм.

Ряд 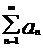называется расходящимся, если последовательность 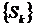его частичных сумм расходится.

Если ряд 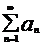сходится, то число 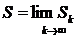называется его суммой, при этом пишут .

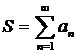Если ряд расходится, то 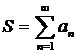и его остаток 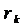любого порядка расходится. Если ряд сходится, то и его остаток k-ого порядка 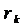при любом k сходится, в этом случае , .

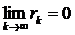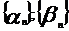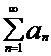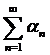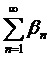Если члены ряда - комплексные числа , где - действительные последовательности , то сходимость ряда эквивалентна одновременной сходимости рядов и и

.

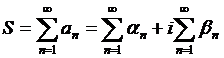Таким образом, исследование свойств рядов с комплексными членами сводится к исследованию рядов с действительными членами.

Пример 1.Рассмотрим ряд

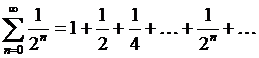
Частичная сумма 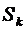этого ряда есть

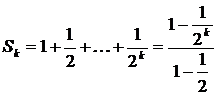
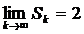. Следовательно, данный ряд сходится, и его сумма равна 2.

Пример 2.

Рассмотрим ряд

Поскольку для этого ряда 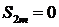, для любого натурального m, то последовательность 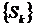не имеет предела. Следовательно, данный ряд расходится.

В большинстве случаев, непосредственный анализ последовательности 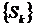не представляется возможным, поэтому основными задачами в теории числовых рядов являются установление сходимости или расходимости данного ряда без вычисления величины его суммы и оценка зависимости остатка ряда 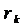от номера k (скорость сходимости ряда).

В силу равенства , оценка 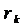даёт оценку погрешности при замене суммы ряда S частичной суммой .

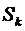Критерий Коши сходимости ряда.

Ряд 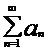сходится тогда и только тогда, когда для любого положительного числа ε найдётся такой номер N=N(ε), что для любых натуральных чисел p и n , n> N(ε), справедливо неравенство

.

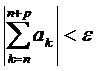Приведём формальную запись критерия Коши сходимости ряда:

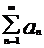сходится .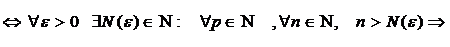

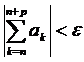Как и при анализе последовательностей, критерий Коши редко применяется для доказательства сходимости конкретного ряда из-за технических трудностей. Область применения критерия Коши – как правило, или утверждения, в которых из сходимости одного ряда выводится сходимость другого, или установление расходимости ряда.

Пример 3.

Пользуясь критерием Коши, покажем, что гармонический ряд 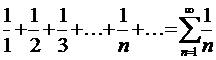расходится. Для этого надо указать такое число 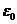>0, что для любого номера N и некоторой пары натуральных чисел p и n, n>N , имеет место неравенство .

Возьмём произвольное натуральное число n .Тогда

.

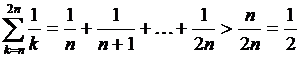Таким образом, для 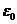=1/2 и произвольного номера N найдены натуральные числа n=N+1 и p=n ,для которых 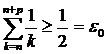, что и требовалось установить. Следовательно, гармонический ряд расходится.