Тема: Действия над комплексными числами.
Цели работы: научиться производить математические операции над комплексными числами.
Краткое изложение темы.
Комплексными числами называются числа вида  , где
, где  и
и  - действительные числа, а число
- действительные числа, а число 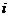 , определяемое равенством
, определяемое равенством  , называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
1) два комплексных числа  и
и  называются равными, если
называются равными, если  и
и  ,
,
2) суммой двух комплексных чисел  и
и  называется комплексное число
называется комплексное число  ,
,
3) произведением двух комплексных чисел  и
и  называется комплексное число
называется комплексное число  .
.
Запись  называется алгебраической формой записи комплексного числа, где
называется алгебраической формой записи комплексного числа, где  - действительная часть,
- действительная часть,  - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
Любое действительное число  содержится в множестве комплексных чисел, его можно записать так:
содержится в множестве комплексных чисел, его можно записать так:  .
.
Числа  и
и  называются комплексно-сопряженными.
называются комплексно-сопряженными.
Числа  и
и  называются противоположными.
называются противоположными.
Модулем комплексного числа называется число  .
.
Аргументом комплексного числа называется угол  между действительной осью
между действительной осью  и вектором
и вектором  , отсчитываемый от положительного направления действительной оси. Записывается так:
, отсчитываемый от положительного направления действительной оси. Записывается так:  или
или  .
.
Из определения тригонометрических функций следует, что если  , то имеют место равенства:
, то имеют место равенства:
 ,
,
 .
.
Действия над комплексными числами  и
и  , заданными в алгебраической форме:
, заданными в алгебраической форме:
сложение:  ,
,
вычитание:  ,
,
умножение:  ,
,
деление:  .
.
Тригонометрическая форма комплексного числа
 .
.
Действия над комплексными числами, заданными в тригонометрической форме:
умножение:
 ,
,
деление:
 ,
,
возведение в 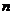 -ю степень:
-ю степень:
 - формула Муавра,
- формула Муавра,
извлечение корня 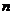 -ой степени
-ой степени
 ,
,
где  - арифметический корень,
- арифметический корень,  .
.
Показательная функция с комплексным показателем
 .
.
В частности, при 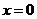 получается соотношение
получается соотношение
 - формула Эйлера.
- формула Эйлера.
Для комплексных показателей остаются в силе основные правила действий с показателями.
Показательная функция имеет период, равный  , т.е.
, т.е.  .
.
Показательная форма записи комплексного числа  .
.
Действия над комплексными числами, заданными в показательной форме:
умножение:
 ,
,
деление:
 ,
,
возведение в 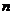 -ю степень:
-ю степень:
 ,
,
извлечение корня 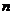 -ой степени
-ой степени
 ,
,
где  - арифметический корень,
- арифметический корень,  .
.
 формулы Эйлера.
формулы Эйлера.
Примеры выполнения заданий.
Пример 1. Найти модуль и главное значение аргумента числа  .
.
Решение:
1. Выполним деление:

2. Найдем модуль данного числа:
 .
.
3. Найдем главное значение аргумента:

Ответ:  ,
,  ,
,  .
.
Пример 2. Представить в тригонометрической форме число:  .
.
Решение:
Найдем модуль числа:  .
.
Найдем главное значение аргумента:

Значит, 
или 
Ответ: 
Пример 3. Возвести в степень  .
.
Решение:
Представим данное число в тригонометрической форме.


Итак,  .
.
По формуле Муавра получим

Ответ: 
Пример 4. Извлечь корни из комплексного числа  .
.
Решение:
Представим число 1 в тригонометрической форме:  .
.
По формуле находим

если  , то
, то  ,
,
если  , то
, то  ,
,
если  , то
, то  .
.
Ответ:  , то
, то  ,
,  , то
, то  ,
,  , то
, то  .
.
Пример 5. Решите уравнение  .
.
Решение:
Введем подстановку  , тогда
, тогда

Вычислим дискриминант  .
.
Найдем корни уравнения  ,
,  .
.
Тогда
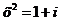 или или   |    |
Ответ:  ,
,  ,
,  ,
,  .
.
Задания для практической работы.
Вариант 1.
1. Найдите модуль и аргумент числа  .
.
2. Выполните действия:  .
.
3. Возведите в степень по формуле Муавра  .
.
4. Извлеките корень  .
.
5. Решите уравнение  .
.
Вариант 2.
1. Найдите модуль и аргумент числа  .
.
2. Выполните действия:  .
.
3. Возведите в степень по формуле Муавра  .
.
4. Извлеките корень  .
.
5. Решите уравнение  .
.
Практическая работа № 9.
