Расчет симметричного сечения

Для изображенного на рисунке 15 сечения определить:

1) главные центральные моменты инерции сечения;

2) главные центральные моменты сопротивления сечения;

3) главные центральные радиусы инерции сечения.

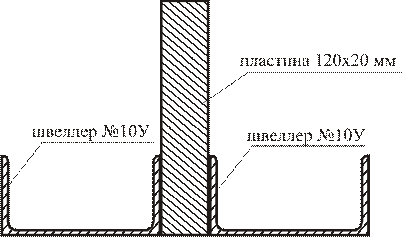
Рисунок 15

Решение.

1). Сечение, изображенное на рисунке 15, является сложным, составленным из двух простейших фигур: швеллера и прямоугольника. Выпишем из справочника геометрические характеристики этих фигур относительно их собственных центральных осей.

Швеллер №10У.

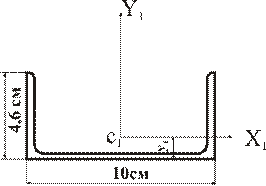
Из сортамента (приложение В, таблица В4):

Площадь швеллера А₁=10,9см^2..

Расстояния от стенки швеллера до центра тяжести т.С₁:

y₁ (в сортаменте z₀)=1,44см.

Осевые моменты инерции швеллера: 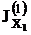(в сортаменте J_Y)=174 см⁴;

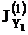(в сортаменте J_X)==20,4 см⁴.

Ось Y₁ параллельна короткой стороне швеллера, поэтому J_Y1>Jx₁.

Центробежный момент инерции швеллера Jx₁y₁=0, так как система координат OX₁Y₁ является главной системой координат швеллера.

Прямоугольник.

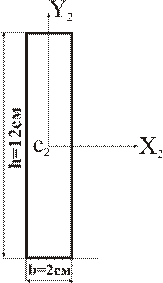
Из таблицы Б1:

Площадь ^..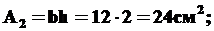

Осевые моменты инерции: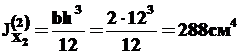

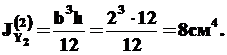
Центробежный момент инерции прямоугольника Jx₂y₂=0, так как система координат OX₂Y₂ является главной системой координат прямоугольника.

2). Изобразим сечение в масштабе (рис.16).

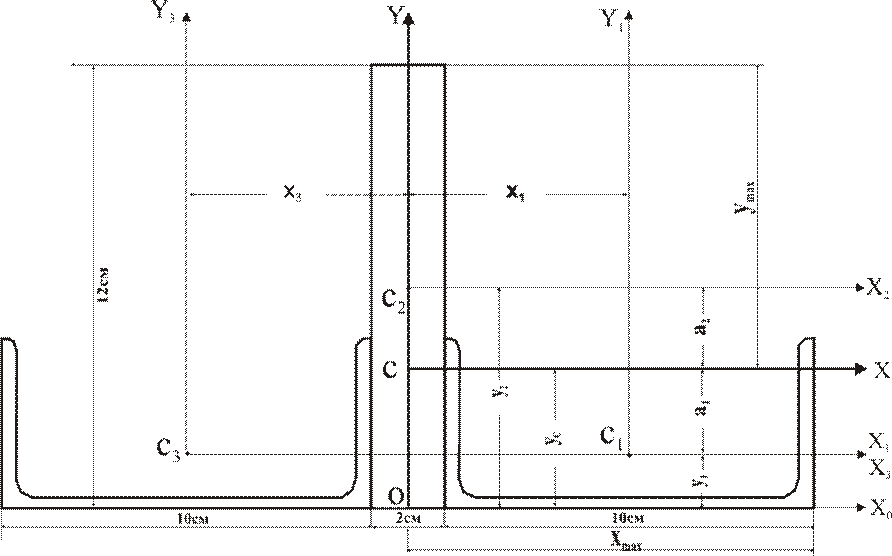
Рисунок 16

3). Выберем произвольную вспомогательную систему координат OX₀Y и найдем координаты центра тяжести сечения т.С относительно этой системы. Так как из чертежа очевидно, что т.С будет лежать на оси Y, то достаточно найти лишь координату y_с.

Выпишем сначала координаты точек С₁, С₂, С₃ относительно осей OX₀Y,.используя чертеж на рисунке 16 и данные 1-го пункта решения:

т.С₁(x₁=1+5=6см; y₁=1,44см);

т.С₂ (x₂=0; y₂=6см).

т.С₃(x₃=-x₁=-6см; y₃=1,44см);

Найдем общую площадь сечения

А=А₁+А₂+А₃=10,9х2+24=45,8см².

По формулам (1):

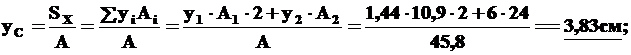
Нанесем на чертеж т.С(0,y_c) и проведем через нее центральную ось CX, параллельную вспомогательной оси OX₀.

Выпишем теперь координаты точек С₁, С₂, С₃ относительно новой оси СX.

Из рисунка 16: a₁=y₁-y_c=1,44-(3,83)=-2,39см;

a₂=y₂-y_c=6-(3,83)=2,17см;

a₃=y₃-y_c=1,44-(3,83)=-2,39см ;

Проверим правильность определения положения центра тяжести сечения. Так как статический момент сечения относительно любой центральной оси должен быть равен нулю, то, используя формулы (2), получим:

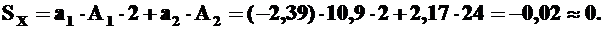
Отсюда следует, что оси X,Y действительно являются центральными, то есть положение центра тяжести найдено правильно. Так как ось CY совпадает с осью симметрии сечения, то, на основании пункта 2.2, система CXY будет главной центральной системой координат сечения.

4). Найдем главные центральные моменты инерции J_X, J_Y.

Согласно соотношению (7), для составного сечения:

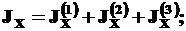(12)

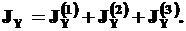
Найдем сначала моменты инерции для швеллера (фигура 1). Так как оси CXY параллельны осям C₁X₁Y₁, а относительно этих осей моменты инерции известны (см. 1-й пункт решения), то применяем формулы (3):

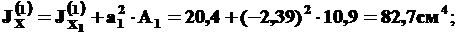
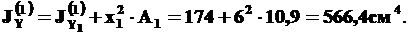
Для второй фигуры (прямоугольника), получим:

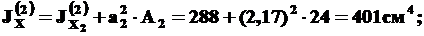
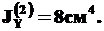
Очевидно, что

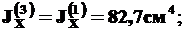
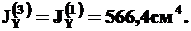
Подставляем найденные значения в (12):

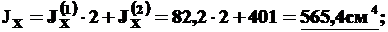
5). Найдем главные центральные моменты сопротивления W_X, W_Y.

Из определения моментов сопротивления сечения

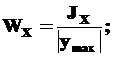
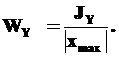
Из чертежа (рис.16) найдем

|x_max|=10+1=11см.

|y_max|=12-y_c=12-3,83=8,17см.

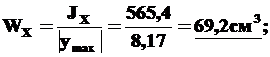
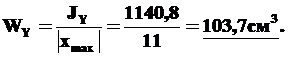
6). Найдем главные центральные радиусы инерции i_X, i_Y.

Из определения радиусов инерции сечения

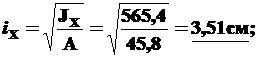
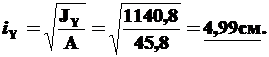
Задача решена.

Приложение А

Расчетно-проектировочная работа «Геометрические характеристики плоских сечений»

Для сечения, симметричного относительно вертикальной оси, составленного из прямоугольников и прокатных профилей, требуется:

1. Вычертить сечение в масштабе и показать основные размеры в числах.

2. Определить положение центра тяжести и указать положение главных центральных осей.

3. Вычислить величину главных центральных моментов инерции сечения и главных центральных моментов сопротивления сечения.

4. Определить величину главных центральных радиусов инерции сечения.

Варианты заданий приведены на страницах 29-31. Числовые данные взять из таблицы А1.

Таблица А1

№	швеллер	двутавр	равнополочный уголок, мм	неравнополочный уголок,мм	пластина, мм
	№8У	№16Б2	25х25х4	70х45х5	150х20
	№10У	№18б2	40х40х4	80х50х5	160х25
	№12У	№20Б1	50х50х5	90х56х8	170х25
	№14У	№23Б1	56х56х5	100х63х10	190х25
	№16У	№26Б1	63х63х6	125х80х7	200х20
	№16аУ	№26Б2	70х70х8	125х80х10	210х20
	№18У	№30Б1	75х75х9	140х90х8	220х25
	№18аУ	№30Б2	80х80х8	140х90х10	250х20
	№20У	№35Б1	90х90х6	160х100х10	250х25
	№22У	№35Б2	90х90х9	160х100х14	260х20
	№24У	№40Б2	110х110х8	180х110х10	280х20
	№27У	№45Б1	125х125х10	200х125х11	300х20
	№30У	№50Б1	125х125х16	200х125х16	320х20
	№33У	№55Б1	140х140х12	250х160х12	350х20
	№36У	№60Б1	160х160х20	250х160х20	400х20
	№10У	№30Б1	40х40х3	50х32х4	120х25
	№12У	№30Б2	45х45х4	56х36х4	130х20
	№14У	№35Б1	50х50х4	63х40х6	140х20
	№16У	№40Б1	56х56х4	75х50х8	150х25
	№18У	№40Б2	63х63х4	80х50х6	160х20
	№20У	№45Б2	70х70х6	110х70х8	170х20

Варианты заданий

Приложение Б

Геометрические характеристики простейших сечений

Таблица Б1 - Геометрические характеристики простейших сечений

Форма сечения	Площадь сечения,	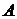Осевые моменты инерции	Осевые моменты сопротивления	Осевые радиусы инерции
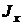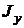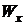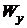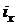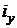Круг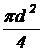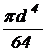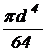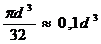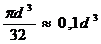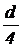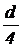
Кольцо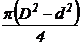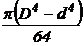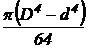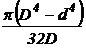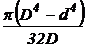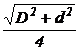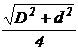

Продолжение таблицы Б1

Форма сечения	Площадь сечения,	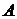Осевые моменты инерции	Осевые моменты сопротивления	Осевые радиусы инерции
Полукруг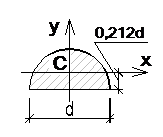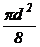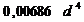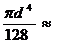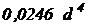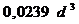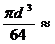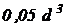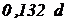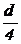
Прямоугольник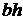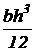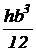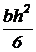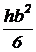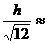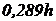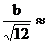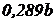

Продолжение таблицы Б1

Форма сечения	Площадь сечения,	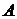Осевые моменты инерции	Осевые моменты сопротивления	Осевые радиусы инерции
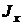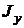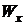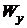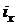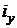Равнобедренный треугольник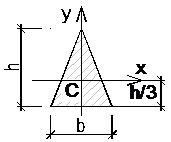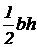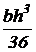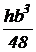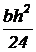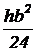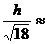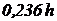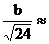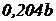
Прямоугольный треугольник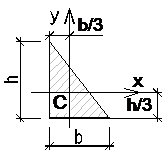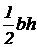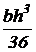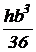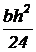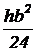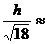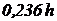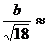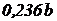

Приложение В