Расчет несимметричного сечения
Для изображенного на рисунке 12 сечения требуется определить главные центральные моменты инерции.

Рисунок 12
Решение.
1). Сечение, изображенное на рисунке 12, является сложным, составленным из двух простейших фигур: неравнополочного уголка и равнобедренного треугольника. Выпишем из справочника геометрические характеристики этих фигур относительно их собственных центральных осей.
Уголок неравнополочный 100х63х10.
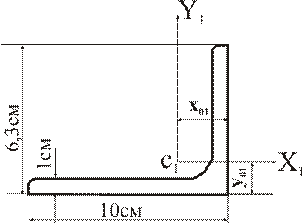
| |
Из сортамента (приложение В, таблица В2):
Площадь уголка А1=15,5см2..
Расстояния от полки и стенки уголка до центра тяжести т.С1:
x01 (в сортаменте y0)=3,4см;
y01 (в сортаменте x0)=1,58см.
Осевые моменты инерции уголка:  (в сортаменте JY)=47,1 см4;
(в сортаменте JY)=47,1 см4;
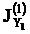 (в сортаменте JX)=154 см4.
(в сортаменте JX)=154 см4.
Ось Y1 параллельна короткой стороне уголка, поэтому JY1>Jx1.
Центробежный момент инерции уголка: 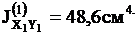 .
.
Знак центробежного момента выбран в соответствии с рисунком 11.
Треугольник равнобедренный.
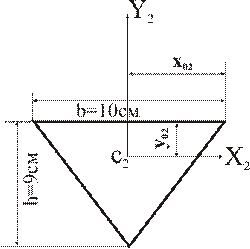
Из таблицы Б1:
Площадь 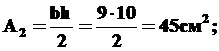 ..
..
Положение центра тяжести т.С2 характеризуется отрезками:
x02 =5см;
y02 =h/3=9/3=3см.
Осевые моменты инерции: 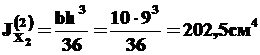
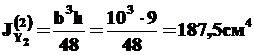
| |
Центробежный момент инерции треугольника Jx2y2=0, так как система координат OX2Y2 является главной системой координат треугольника.
2). Изобразим сечение в масштабе (рис.13).
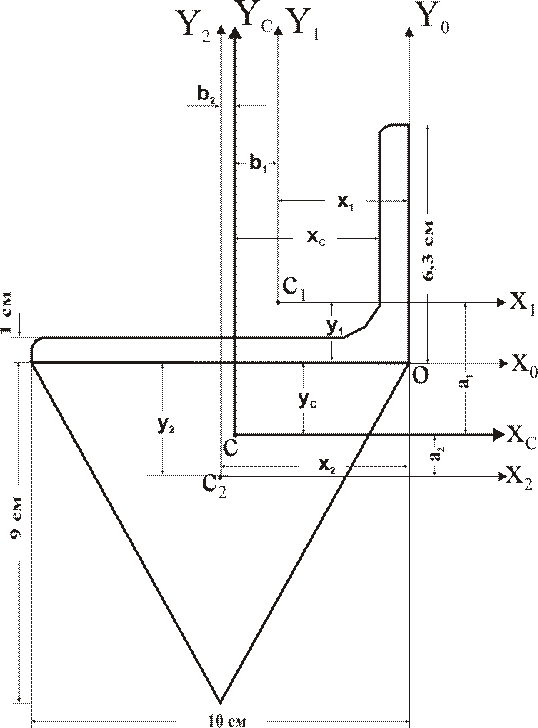
Рисунок 13
| |
3). Выберем произвольную вспомогательную систему координат OX0Y0 и найдем координаты xc,yc центра тяжести сечения т.С относительно этой системы.
Выпишем сначала координаты точек С1 и С2 относительно осей OX0Y0,используя чертеж на рисунке 13 и данные 1-го пункта решения:
т.С1(x1=-x01=-3,4см; y1=y01=1,58см);
т.С2 (x2=-x02=-5см; y2=-y02=-3см).
Найдем общую площадь сечения
А=А1+А2=15,5+45=60,5см2.
По формулам (1):
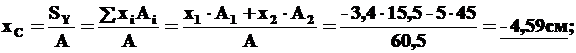
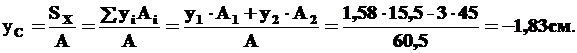
Нанесем на чертеж точку С(xc,yc) и проведем через нее центральные оси CXCYC, параллельные вспомогательным осям OX0Y0.
Выпишем теперь координаты точек С1 и С2 —ai, bi —относительно новых осей СXсYс.
Из рисунка 13: a1=y1-yc=1,58-(-1,83)=3,41см;
b1=x1-xc=-3,4-(-4,59)=1,19см;
a2=y2-yc=-3-(-1,83)=-1,17см;
b2=x2-xc=-5-(-4,59)=-0,41см.
Проверим правильность определения положения центра тяжести сечения. Так как статический момент сечения относительно любой центральной оси должен быть равен нулю, то, используя формулы (2), получим:
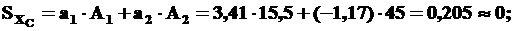

Отсюда следует, что оси Xc,Yc действительно являются центральными, то есть положение центра тяжести найдено правильно.
4). Найдем центральные моменты инерции Jxс, Jyс, Jxсyс.
Согласно соотношению (7), для составного сечения:
| |
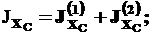
 (8)
(8)

Найдем сначала моменты инерции для уголка (фигура 1). Так как оси CXCYC параллельны осям C1X1Y1, а относительно этих осей моменты инерции известны (см. 1-й пункт решения), то применяем формулы (3):
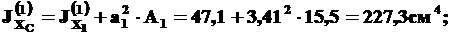
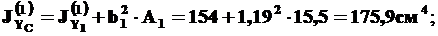 (9)
(9)

Аналогично для второй фигуры (треугольника), получим:
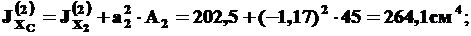
 (10)
(10)

Подставим (9) и (10) в (8):
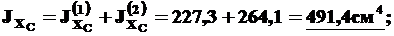
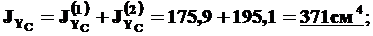 (11)
(11)

5). Найдем положение главных центральных осей CXY. Для этого используем формулу (5):
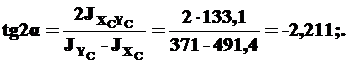
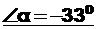 .
.
Угол α меньше нуля, поэтому откладываем его от оси СXс по часовой стрелке и проводим главные центральные оси CXY (рис.14).
| |
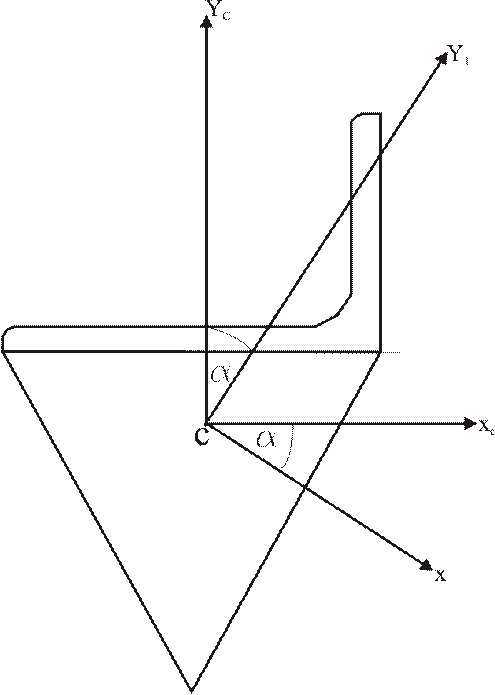
Рисунок 14
6). Найдем главные центральные моменты инерции Jx, Jy. Для этого используем формулу (6):
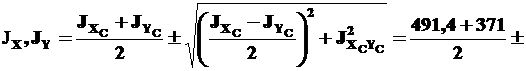
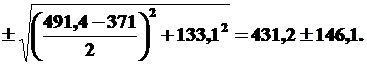
| |
Отсюда получаем:

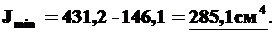
Поскольку для данного сечения Jx1y1 > 0, то ось, относительно которой момент инерции максимален проходит через вторую и четвертую. четверти системы координат CXCYC, то есть


Проверка.
Найдем главные центральные моменты инерции по формулам (4), полагая в них α=-330:
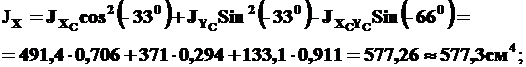
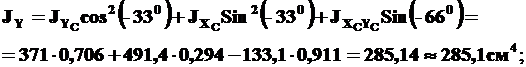

Задача решена.
| |
