МО задачи пространственной ориентации объекта
(непрерывные алгоритмы задачи ориентации – см. п.6.2 Л.6, фор. (6.7)…(6.9), (6.12) или (6.17)…(6.21))
Константы:
dT=0.005 с;
weight_Or=[weight_b;weight_b;weight_a];– веса текущих оценок погрешностей ориентации;
Входные переменные:
Lhb_o - %начальное значение кватернионаLhb,поступающее из задачи начальной («грубой») ориентации объекта;
dfb1(j+1)=[dfxb1;dfyb1;dfzb1]– текущие значения вектора квазикоординат – первого интеграла от вектора угловой скорости в проекциях на связанные оси (оси ИБ БИИМ), формируемые с дискретностью dTв задаче формирования приращений вектора квазикоординат;
dfb2(j+1)=[dfxb2;dfyb2;dfzb2]–текущие значения вектора квазикоординат - второго интеграла от вектора угловой скорости в проекциях на связанные оси (оси ИБ БИИМ), формируемые с дискретностью dTв задаче формирования приращений вектора квазикоординат;
Ro(j+1) -текущее значение с дискретностью dTугла поворота ИБ относительно осей корпуса БИИМ (объекта), (поворот вокруг оси Zo , положительное направление - против часовой стрелки);
Omh_(j)=[OmE_;OmN_;OmH_]- значения вектора угловой скорости вращения географического трехгранника с предыдущего цикла (шага), формируемые в задаче преобразования сигналов ЛА на навигационные оси и интегрирования;
FKOr(j)=[beta;gamma;alpha] –значенияоценок погрешностей ориентации из предыдущего цикла dT (на предыдущем шаге), формируемые в задаче выработки корректур с использованием ФК с дискретностью Tz(см. Л.12).
Примечание:Когда фильтровая задача с использованием ФК не решается, тоFKOr(j)=0и используются
, 
, 
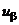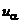-непрерывные управления, формируемые в задаче выработки корректур с использованием стационарных фильтров (см. п. 9.2,Л.9);
Выходные переменные:
Cbh(j+1) –матрица ориентации для перехода от связанных осей (осей ИБ БИИМ) к горизонтной системе координат с географической ориентацией осей;
K(j+1) -текущие значения курса объекта;
Psi(j+1), Teta(j+1) –текущие значения углов килевой и бортовой качки объекта;
Алгоритм задачи, решаемой с дискретностью dT:
%Формирование вектора Fb Эйлера по квазикоординатам dfb1, dfb2:
[dfxb1;dfyb1;dfzb1]=dfb1(j+1);
Mdfb1=[ 0 (-1)*dfzb1 dfyb1;
dfzb1 0 (-1)*dfxb1;
(-1)*dfyb1 dfxb1 0 ];
Fb=dfb1 - Mdfb1*dfb2/dT;
[Fx;Fy;Fz]=Fb;
%Формирование кватерниона HH(i,b)
F2=(Fx^2+Fy^2+Fz^2)/4;
F3=(6-F2)/12+(F2^2)/240;
HH=[1-F2/2+(F2^2)/24;
F3*Fx;
F3*Fy;
F3*Fz];
%Формирование вектора Fh Эйлера по Omh(j)_
[OmE_;OmN_;OmH_]=Omh_(j);
OmE=OmE_- ;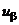
OmN=OmN_- ;
OmH=OmH_- 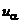; -при формировании непрерывных управлений с использованием стационарных фильтров;
OmE=OmE_ - weight_b*beta*1/Tz;
OmN=OmN_ - weight_b*gamma*1/Tz;
OmH=OmH_ - weight_a*alpha*1/Tz; -при формировании управлений с использованием дискретного фильтра Калмана;
Omh(j)=[OmE;OmN;OmH];
dfh1(j+1)=Omh(j)*dT;
dfh2(j+1)=Omh(j)*dT^2/2;
[dfE1;dfN1;dfH1]=dfh1;
Mdfh1=[ 0 (-1)*dfH1 dfN1;
dfH1 0 (-1)*dfE1;
(-1)*dfN1 dfE1 0 ];
Fh=dfh1 - Mdfh1*dfh2/dT;
[FE;FN;FH]=Fh;
%Формирование кватерниона FF(h,i)
F4=(FE^2+FN^2+FH^2)/4;
F5=(6-F4)/12+(F4^2)/240;
FF=[1-F4/2+(F4^2)/24;
(-1)*F5*FE;
(-1)*F5*FN;
(-1)*F5*FH];
[FF1;FFE;FFN;FFH]=FF;
%Формирование кватерниона Lhb
MFF=[FF1 (-1)*FFE (-1)*FFN (-1)*FFH;
FFE… FF1 (-1)*FFH FFN;
FFN FFH FF1 (-1)*FFE;
FFH (-1)*FFN FFE FF1];
FFL(j+1)=MFF(j+1)*L(j);
[FFLO;FFL1;FFL2;FFL3]=FFL;
MFFL=[FFLO (-1)*FFL1 (-1)*FFL2 (-1)*FFL3;
FFL1… FFLO (-1)*FFL3 FFL2;
FFL2 FFL3 FFLO (-1)*FFL1;
FFL3 (-1)*FFL2 FFL1 FFLO];
L_(j+1)=MFFL(j+1)*HH(j+1);
[L1_;L2_;L3_;L4_]=L_(j+1);
mL_^2=L1_^2+L2_^2+L3_^2+L4_^2;
L(j+1)=L_(j+1)+(1/2)*(1-mL_^2)*L_(j+1);
%Формирование матрицы Cbh
[L1;L2;L3;L4]=L(j+1);
c11=L1^2+L2^2 - L3^2 - L4^2;
c12=2*(L2*L3 – L1*L4);
c13=2*(L2*L4+L1*L3);
c21=2*(L2*L3+L1*L4);
c22=L1^2+L3^2 – L2^2 - L4^2;
c23=2*(L3*L4 – L1*L2);
c31=2*(L2*L4 – L1*L3);
c32=2*(L3*L4+L1*L2);
c33=L1^2+L4^2 – L2^2 – L3^2;
Cbh=[c11 c12 c13;
c21 c22 c23;
c31 c32 c33];
%Формирование матрицы Coh(j+1)
Cob=[cos(Ro) sin(Ro) 0;
(-1)*sin(Ro) cos(Ro) 0;
0 0 1];
Coh=Cbh*Cob;
[d11 d12 d13;
d21 d22 d23;
d31 d32 d33]=Coh;
%Формирование углов качки и курса
Psi=atan(d32/sqrt(1 – d32^2));
Teta=atan( - d31/d33);
K=atan2(d12/d22);
При
atan2<0
K=atan2(d12/d22)+2*pi;
4.4. МО задачи преобразования сигналов ЛА на навигационные оси и интегрирования
(непрерывные алгоритмы задачи преобразования сигналов акселерометров и выработки параметров поступательного движения – см. п.6.4 Л.6, фор. (6.41)…(6.44))
Константы:
dT=0.005 с;
go=9.780318;% м/с2-ускорение силы тяжести на экваторе;
bet=0.0053024;
bet_1=0.0000059;
U=7.292116e-5; %угловая скорость суточного вращения Земли;
%параметры земного эллипсоида (Красовского)
a=6378245 м;%большая полуось
e2=0.0066934; % квадрат эксцентриситета
weight_DV=[weight_DVE 0 0
0 weight_DVN 0
0 0 weight_DVH]
- веса текущих оценок погрешностей составляющих вектора линейной скорости;
weight_DFi;weight_DLa;weight_Dh - веса текущих оценок погрешностей координат места ИММ;
Входные переменные:
b1(j+1)=[b1xb;b1yb;b1zb]- приращения составляющих вектора кажущейся линейной скорости в связанных осях (осях ИБ БИИМ), (поступают с дискретностью dTиз задачи формирования приращений векторов кажущихся линейной скорости и линейного перемещения);
b2(j+1)=[b2xb;b2yb;b2zb]- приращения составляющих вектора кажущегося линейного перемещения в связанных осях (осях ИБ БИИМ), (поступают с дискретностью dTиз задачи формирования приращений векторов кажущихся линейной скорости и линейного перемещения);
Cbh –значенияматрицы ориентации для перехода от связанных осей (осей ИБ БИИМ) к горизонтной системе координат с географической ориентацией осей (формируются в задаче ориентации);
Vho=[VEo;VNo;VHo] – значения составляющих вектора линейной скорости в начальный момент времени;
FLho=[Fio;Lao;ho] – значения координат места БИИМ в начальный момент времени;
FKDV(j)=[FKDVE;FKDVN;FKDVH] - значенияоценок погрешностей скорости из предыдущего цикла dT (на предыдущем шаге), формируемые в задаче выработки корректур с использованием ФК с дискретностью Tz(см. Л.12).;
FKDFLh(j)=[FKDFi;FKDLa;FKDh] - значенияоценок погрешностей координат из предыдущего цикла dT (на предыдущем шаге), формируемые в задаче выработки корректур с использованием ФК с дискретностью Tz(см. Л.12).;
Примечание:Когда фильтровая задача с использованием ФК не решается, тоFKDV(j)=0; FKDFLh(j)=0и используются
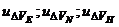-непрерывные управления и разовые коррекции 
, формируемые в задаче выработки корректур с использованием стационарных фильтров (см. п. 9.2,Л.9).
Выходные переменные:
Vh(j+1) -значения вектора линейной скорости в проекциях на оси горизонтной системы координат с географической ориентацией осей;
DSh(j+1) - значения приращений на конечном интервале временивектора линейных перемещений в проекциях на оси горизонтной системы координат с географической ориентацией осей;
Fi(j+1) –широта места;
La(j+1) –долгота места;
h(j+1) –высота;
Omh_(j+1)=[OmE_;OmN_;OmH_] -значения вектора угловой скорости вращения географического трехгранника.
Алгоритм задачи, решаемой с дискретностью dT:
% «Вредные» ускорения
BAe(j+1)=VH(j)*(2*U+dLa(j))*cos(Fi(j)) - VN(j)*(2*U+dLa(j))*sin(Fi(j));
BAn(j+1)=VE(j)*(2*U+dLa(j))*sin(Fi(j))+VH(j)*dFi(j);
ge=go*(1+bet*(sin(Fi))^2-bet_1*(sin(2*Fi))^2);
BAh(j+1)=ge - VE(j)*(2*U+dLa(j))*cos(Fi(j)) - VN(j)*dFi(j);
BA=[BAe;BAn;BAh];
% Вычисление составляющих вектора линейной скорости и приращений линейных перемещений
dC(j+1)=(Cbh(j+1) - Cbh(j))/dT;
dVkh(j+1)=Cbh(j+1)*b1(j+1) - dC(j+1)*b2(j+1);
dVh(j+1)=dVkh(j+1) – BA*dT;
Vh(j+1)=Vh(j)+dVh(j+1) - [ 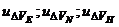]*dT;
- при формировании непрерывных управлений с использованием стационарных фильтров;
Vh(j+1)=Vh(j)+dVh(j+1) – weight_DV*FKDV(j)*dT/Tz; %- при формировании управлений с использованием дискретного фильтра Калмана;
[VE;VN;VH]=Vh(j+1);
При j=0
Vh(j)=Vho;
dSkh(j+1)=Cbh(j+1)*b2(j+1);
dSh(j+1)=Vh(j)*dT+dSkh(j+1) – (1/2)*BA*dT^2;
% Вычисление приращений декартовых координат и географических координат
DSh(j+1)=DSh(j)+dSh(j+1);
[DSE;DSN;DSH]=DSh;
При j=0
DSh(j)=0;
La(j+1)=La(j)+dSE(j+1)/(R*cos(Fi(j+1))) -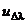 
*dT;
Fi(j+1)=Fi(j)+dSN(j+1)/R -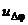 
*dT;
h(j+1)=h(j)+dSH(j+1) -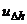 
*dT;% - при формировании разовых коррекций по данным обсервации;
La(j+1)=La(j)+dSE(j+1)/(R*cos(Fi(j+1))) – FKDLa(j)*weight_DLa*dT/Tz;
Fi(j+1)=Fi(j)+dSN(j+1)/R – FKDFi(j)*weight_DFi*dT/Tz;
h(j+1)=h(j)+dSH(j+1) – FKDh(j)*weight_Dh*dT/Tz; %- при формировании управлений с использованием дискретного фильтра Калмана;
При j=0
La(j)=Lao; Fi(j)=Fio; h(j)=ho;
% Вычисление радиусов кривизны для эллипсоида (общеземного или Красовского)
RE=(a/sqrt(1-e2*(sin(Fi))^2))+h;
RN=(a*(1-e2)/sqrt((1-e2*(sin(Fi))^2)^3))+h;
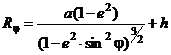
% Вычисление угловых скоростей
dLa(j+1)=VE(j+1)/(RE*cos(Fi(j+1)));
dFi(j+1)=VN(j+1)/RN;
OmE_(j+1)= - dFi(j+1);
OmN_(j+1)=(U+dLa(j+1))*cos(Fi(j+1));
OmH_(j+1)=(U+dLa(j+1))*sin(Fi(j+1));
Omh_(j+1)=[OmE_;OmN_;OmH_];