Постановка транспортной задачи общего вида

Наиболее часто в практической деятельности человеку приходится встречаться с задачами о распределении транспортных потоков. Пример простейшей задачи транспортного типа рассмотрен в § 2.2.

Классическая постановка транспортной задачи общего вида такова.

Имеется пунктов отправления – «поставщиков» и пунктов потребления – «потребителей» некоторого одинакового товара. Для каждого пункта определены:

объемы производства -го поставщика,

спрос -го потребителя, ;

стоимость перевозки одной единицы продукции из пункта – i-го поставщика, в пункт – j-го потребителя.

Обычно данные удобно представлять в виде таблицы, которую называют таблицей стоимостей перевозок

Поставщики	Потребители	В1	В2	…	Вn	запасы
А1	C11	C12		C1n	a1
А2	C21	C22		C2n	a2
Аm	Cm1	Cm2		Cmn	am
Потребности	b1	b2		bn

Требуется в задаче найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при данных запасах поставщиков, и суммарные транспортные расходы были бы минимальными.

Под планом перевозок понимают объем перевозок – количество товара, которое необходимо перевезти от -го поставщика к -му потребителю. Для построения математической модели задачи необходимо ввести штук переменных каждая переменная обозначает объем перевозок из пункта в пункт . Набор переменных и будет планом, который необходимо найти, исходя из постановки задачи.

Ограничения задачи примут вид (3.1):

Очевидно, что для разрешимости задачи (3.1) необходимо, чтобы суммарный спрос не превышал объемы производства у поставщиков: . Если это неравенство выполняется строго, то задача называется «открытой» или «несбалансированной». Если же , то задача называется «закрытой» транспортной задачей.

Мы остановимся сейчас на решении закрытых транспортных задач (ЗТЗ).

В силу ограничений (3.1) нетрудно увидеть, что ТЗ является задачей ЛП и может быть решена симплекс–методом после приведения ее к специальному виду. Но структура системы ограничений имеет некоторую специфику, а именно каждая переменная входит ровно два раза в неравенства системы и все переменные входят в неравенства системы с коэффициентом 1. В силу этой специфики разработан собственный метод решения, называемый методом потенциалов. По–прежнему идеей является переход от одного опорного плана к другому, обязательно «лучшему», с точки зрения значения целевой функции. Здесь целевая функция последовательно уменьшает свои значения, т.к. цель задачи – минимизировать расходы. Каждому опорному плану также соответствует своя распределительная таблица. Переход осуществляется, пока полученный план не будет удовлетворять условию оптимальности. Сначала необходимо построить первоначальный опорный план. В качестве первоначального плана годится любое решение системы уравнений (3.1). Заметим, что это система линейных уравнений, состоящая из уравнений, с неизвестными. Можно доказать, что линейно–независимых уравнений в системе (3.1) , ввиду условия сбалансированности, т.е. базисных переменных должно быть , остальные будут нулевыми. Итак, в качестве плана будем представлять себе таблицу размера , в которой должно быть занято ровно клеток, отвечающих базисным переменным . Стоимости перевозок всегда будем записывать в правом верхнем углу ячейки таблицы, естественно считая их постоянными на протяжении решения задачи.

Алгоритм метода потенциалов

Алгоритм состоит из трех основных шагов:

1) построение первоначального опорного плана.

2) проверка плана на оптимальность.

3) улучшение плана.

Шаг 1. Построение первоначального опорного плана.

Существует два наиболее часто применяемых метода для нахождения первого плана: метод наименьшей стоимости и метод северо-западного угла. Метод наименьшей стоимости позволяет найти план, наиболее близкий к оптимальному, метод северо-западного угла легче программируется, и поэтому до сих пор «живет». Но, если вы решаете задачу «вручную», то применение метода наименьшей стоимости, как правило, уменьшает количество итераций.

Идея метода наименьшей стоимости проста и отражается в названии метода. Сначала следует организовать перевозки к тем поставщикам, где стоимость минимальна. Рассмотрим конкретный пример.

Транспортная задача. Пусть имеется 4 поставщика некоторой продукции и 5 потребителей. Стоимости перевозок от i-го поставщика к j-му потребителю, а также потребности потребителей и возможности поставщиков заданы табл. 3.1

Таблица 3.1

	В1	В2	В3	В4	В5	запасы
А1
А2
А3
А4
потребности

Эта транспортная задача является закрытой или сбалансированной, т.к. 24+12+18+16=60 и 11+13+26+10+10=60 – потребности равны запасам. Будем заполнять первую распределительную таблицу. Стоимости перевозок в новой таблице будем располагать в правом верхнем углу клеток, а в центр клеток помещать числа, соответствующие первоначальному опорному плану перевозок.

Итак, минимальная стоимость перевозки – это число 1, оно встречается на двух местах, с номерами (2, 4) и (3, 2). Выберем любое, к примеру, (2, 4). Рассуждаем: у поставщика 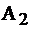имеется запас товара 12 ед., а потребителю 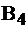требуется 10 ед., можем удовлетворить его потребности и привезти ему 10. Тогда у 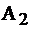останется в запасах 12-10=2 ед. Поместим в клетку (2, 4) наименьшее из чисел 10 и 12, т.е. перевозку 10. При этом заметим, потребности потребителя 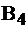удовлетворены, можем вычеркнуть 4-й столбец из рассмотрения, запомнив сбоку, что запасов осталось на втором складе 2 ед. (см.табл. 3.2).

Таблица 3.2

	В1	В2	В3	В4	В5	запасы
А1	21	19	11	-12	12
А2	26	29	14	10 1	26	12/2
А3	39	1	22	- 8	25
А4	53	23	40	-26	28
потребности				10/0

В табл. 3.2 теперь снова ищем минимальный по стоимости элемент, это опять 1 на месте (3, 2). Записываем в эту клетку число 13, как наименьшее из чисел 13 и 18 и вычеркиваем 2-й столбец, потребности В₂ удовлетворены (табл. 3.3).

Таблица 3.3

	В1	В2	В3	В4	В5	запасы
А1	21	19	11	- 12	12
А2	26	29	14	10 1	26	12/2
А3	39	131	22	- 8	25	18/5
А4	53	23	40	– 26	28
потребности		13/0		10/0

Следующее минимальное число по стоимости в таблице после двух вычеркиваний – это число 11 на месте (1, 3). Вписываем в клетку перевозку 24 и вычеркиваем 1-ю строку, запасы у поставщика исчерпаны. Переходим к клетке (2, 3) с минимальной стоимостью 14. Помещаем туда число 2, т.к. в 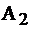имеется 12 единиц продукции, но 10 из них мы уже вывезли в 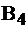, осталось 2 ед. При этом вычеркиваем и столбец, и строку. Далее заполняем клетку (3, 5), сюда мы можем перевезти 5 единиц груза, т.к. 13 уже вывезли в , и у возможности исчерпаны, вычеркиваем 3-ю строку. Затем заполняем клетку (4, 5), поместим туда 5 единиц груза, т.к. 5 уже вывезли в , а ему всего необходимо 10. После всех вычеркиваний в таблице осталась одна клетка (4, 1), поместим туда число 11, что соответствует потребностям и возможностям . Имеем табл. 3.4.

Проверим, что сумма чисел построчно и по столбцам совпадает с возможностями и потребностями. Число занятых клеток соответствующих базисным переменным опорного плана, обязано равняться . Но иногда занятых клеток может оказаться меньше. У нас клеток, занятых перевозками 7. В этом случае на втором шаге алгоритма добавляют в одну из ячеек таблицы фиктивную нулевую перевозку, например в (3, 4), смотри табл.3.4. При выборе клетки руководствуются соображениями минимальной стоимости, а также, чтобы в каждой строке и каждом столбце была по крайней мере одна занятая клетка.

Таблица 3.4

	В1	В2	В3	В4	В5	запасы
А1	21	19	11 24	12	12
А2	26	29	14	1	26
А3	39	1	22	8	25 5
А4	53	23	40	26	28
потребности

Итак, первоначальный план построен. Обычно, проводя построение плана, всё делают в одной таблице, производя в ней все необходимые вычеркивания. Чтобы не загромождать запись, рассуждения проводятся устно.

Шаг 2. Проверка плана на оптимальность.

При построении первоначального плана мы ставим задачу найти хоть какой-нибудь, не обязательно лучший план, удостоверяющий ограничениям задачи. Теперь нам хотелось бы уметь отвечать на вопрос: является ли найденный опорный план оптимальным И если не является, то как «улучшать» его. Эту задачу решает метод потенциалов, предложенный в 1949 г. советскими учеными Л.В. Канторовичем и М.К. Гавуриным, теоретической основой метода является теорема.

Теорема. Если для некоторого опорного плана транспортной задачи можно подобрать систему из чисел , называемых потенциалами, то план оптимален тогда и только тогда, когда выполняются условия:

1) для всех (*)

2) для всех (**)

где – матрица стоимостей перевозок.

Доказательство теоремы опускаем, оно основывается на рассмотрении двойственной задачи к исходной транспортной. Числа, называемые потенциалами, в точности являются переменными двойственной задачи, а сформулированные условия (**) –суть второй теоремы двойственности.

Покажем, как находить числа, называемые потенциалами. Отведем им место в таблице – правый столбец и нижняя строка. Условие (*) представляет собой систему из линейных уравнений с неизвестными потенциалами. Поэтому одно из неизвестных полагаем равным 0 для определенности, затем последовательно находим остальные потенциалы.

Проведем эти вычисления, записывая найденные потенциалы в дополнительно зарезервированный столбец и строку (табл.3.5).

Таблица 3.5

	В1	В2	В3	В4	В5	uj
А1	21	19	11 24	12	12
А2	26	29	14 2	1 10	26
А3	39	1 13	22	8 0	25 5
А4	53 11		40	26	28 5
vi		–49	–29	–42	–25

Проводя вычисления, смотрим только на занятые клетки и на числа, стоящие в правом верхнем углу, – стоимости перевозок.

1. Полагаем один из потенциалов равным 0. Пусть найдем из условия (*) остальные, последовательно обходя занятые клетки:

для занятой клетки (4,1): т.е. ,

для занятой клетки (4,5): т.е. ,

для клетки (3,5): , т.к. ,

затем можем найти из (3,2): , т.к. ,

после из (3,4): , т.к. ,

из (4,2): , т.к.

и, наконец, из (2,3): , т.к. ,

из (3,1): т.к.

Все потенциалы найдены. Вычисления обычно проводятся устно, с особой внимательностью, не путая стоимости перевозок стоящие в правых верхних углах клеток, с самими перевозками стоящими в клетках. Их значения на этом шаге нам не нужны, важно лишь, что они определяют занятость клетки.

2. После нахождения системы потенциалов можно собственно и заняться проверкой плана на оптимальность, ради чего мы и вычисляли потенциалы. Для проверки плана на оптимальность необходимо проверить условие (**). Нужно для свободных клеток посчитать суммы и сравнить их с числами – стоимостями перевозок. Если то по теореме, план является оптимальным, задача решена. Иначе, если хотя бы для одной клетки план нужно улучшать. Переходить к 3-му шагу алгоритма. Сделаем проверку условия (**) для нашей таблицы, записывая в правом верхнем углу выполнение неравенств (табл.3.6).

Таблица 3.6

	В1	В2	В3	В4	В5	vj
А1	40>21	–9<19	11=11 24	–2<12	15>12
А2	43>26	–6<29	14=14 2	1=1 10	18<26
А3	50<39	1=1 13	21<22	8=8 0	25=25 5
А4	53=53 11	4<23	14<40	11<26	28=28 5
ui		–49	–29	–42	–25

В нашей задаче первоначальный опорный план неоптимален, условие (**) нарушено в клетках (1, 1), (1, 5), (2, 1), (3, 1).

Шаг 3. Улучшение плана.

Для проведения операции улучшения плана нам понадобится понятие цикла – контура перераспределения ресурсов.

Циклом будем называть набор клеток таблицы, в котором две и ровно две соседние клетки расположены в одной строке или в одном столбце, вершины поочередно обозначаются «+» и «-». Цикл начинается со свободной клетки и проходит только по занятым.

Графически нетрудно представить цикл в виде ломаной, каждое звено которой лежит в строке или в столбце, причем в каждой строке или столбце не более чем по одному звену. Звенья ломаной располагаются под прямым углом. Цикл начинается со свободной клетки, в которой нарушено условие оптимальности, и проходит только по занятым.

Примеры циклов:

с11	с12	с13 ·	с14 ·			с11 •	с12 •	с13	с14
с21	с22 ·	с23	с24 ·			с21	с22 •	с23	с24 •
с31	с32 ·	с33 ·	с34			с31 •	с32	с33	с34 •

С понятием цикла связаны важные свойства планов:

1) допустимый план является опорным, когда из занятых этим планом клеток нельзя образовать ни одного цикла;

2) если имеем опорный план, то для каждой свободной клетки можно образовать единственный цикл, содержащий данную клетку и некоторые из занятых.

Улучшение плана производится по следующей схеме. В подчеркнутых клетках табл. 3.6. находим клетку с наибольшей разностью т.е. где условие (**) нарушается максимально. Затем для этой клетки согласно свойству 2 строим единственный цикл. Набор клеток в цикле помечаем поочередно знаками «+» и «–», начиная с «+» в свободной клетке. Имеем таблицу 3.7

Таблица 3.7

	В1	В2	В3	В4	В5	запасы
А1	40>21 +	–9<19	11=11 – 24	2<12	15>12
А2	43>26	–6<29	14=14 + 2	1=1 –10	18<26
А3	50>39	1=1 13	21<22	8=8 + 0	25=25 – 5
А4	53=53 –11	4<23	14<40	11<26	28=28 + 5
потребности

Начиная с клетки (1, 1), где условие (**) нарушено максимально, строим цикл. Клетку (1, 1) помечаем знаком «+», далее ходим по занятым клеткам, поворачивая под прямым углом, знаки чередуем, пока не попадем в тот столбец или строку, откуда начали. Если вы нашли цикл, то он верный, т.к. цикл единственен. У нас все занятые клетки вошли в цикл, но это необязательно.

Рассмотрим элементы плана , расположенные в клетках цикла со знаком «–» : . Выберем из них наименьший обозначим Строим новый план по правилу

Новый план записываем в табл. 3.8. Клетка, в которой разница равна 0, у нас (3, 5), теперь будет свободной. Проверьте, что число занятых клеток по-прежнему равно 8.

Таблица 3.8

	В1	В2	В3	В4	В5	запасы
А1
А2
А3
А4
потребности

Очевидно, что полученный план будет удовлетворять прежним ограничениям, т.к. сдвиг перевозки происходит по циклу, а значит, не нарушает суммарную перевозку по столбцу и по строке (в одном месте прибавили, а в другом – столько же отняли). Общая же стоимость перевозок уменьшается на число, равное где – объем перевозок, перемещаемый по циклу. У нас эта величина равна 5·(40–21)=5·19=95.

Действительно, для плана Х общая суммарная стоимость перевозки: .

Для нового плана

=5·21+19·11+7·14+5·1+13·1+5·8+6·53+10·28=1068.

Итак, мы построили новый «лучший» план, 3-й шаг закончен. И теперь переходим к следующей итерации: находим новые потенциалы, проверяем план на оптимальность, улучшаем, если план неоптимален.

Для нашей задачи проведем дальнейшее решение. Новая система потенциалов записана в табл. 3.9.

Условие (**) не выполняется в клетках (4, 3) и (4, 4). С клетки (4, 4) начинаем строить цикл. Выбираем наименьшее из чисел .

Таблица 3.9

	В1	В2	В3	В4	В5	vj
А1	21 + 5	–19<19	11 – 19	–2<12	–4<12
А2	24<26	–6<29	14 + 7	1 – 5	–1<26
А3	31<39	1 13	21<22	8 5	6<25
А4	53 – 6	23=23	43>40	30>26 +	28 10
ui		–30	–10	–23	–25

Строим новый план, добавляя Δ к клеткам с «+», и вычитая Δ из клеток с «–». Новый план выглядит как показано в табл.3.10.

Таблица 3.10

	В1	В2	В3	В4	В5	vj
A1	21 + 10	–13>19	11 – 14	–6<12	–4<12
A2	24<26	–10<29	14 12	–3<1	–1<26
A3	35<39	1	–25<22	8	10<25
A4	53 – 1	19<23	43>40 +	26	28 10
ui		–34	–10	–27	–25

Найдем новую систему потенциалов, запишем в таблицу 3.10.

Оказывается, план не оптимален, в клетки (4, 3) нарушается неравенство (**), еще раз строим цикл, улучшаем план, Δ=1.

Находим новую систему потенциалов (табл. 3.11), проверяем на оптимальность, убеждаемся, что полученный план оптимален.

Таблица 3.11

	В1	В2	В3	В4	В5	vj
A1	21 11	–10<19	11 13	–3<12	–1<12
A2	24<26	–7<29	14 12	0<1	2<26
A3	32<39	1 13	22=22	8 5	10<25
A4	50<53	19<23	40 1	26 5	28 10
ui		­31	–10	–24	–22	–62

Итак, предложенный таблицей 3.11, план перевозок является оптимальным, при этом суммарная стоимость перевозок .

Действительно, после второй итерации стоимость перевозок уменьшилась на величину (30–26)·5=20, после третьей (43–40)·1=3, т.е. 1068–23=1045, что мы и имеем. Задача решена.

Замечание.Если транспортная задача является задачей открытого типа, в которой условие баланса не выполняется, а именно сумма запасов больше суммы потребностей, то решить такую задачу можно по предложенной схеме методом потенциалов, введя дополнительного потребителя, с потребностью равной разности балансов, и нулевыми стоимостями перевозок от каждого поставщика к этому потребителю.