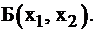Решение задачи линейного программирования графически

Итак, мы научились решать системы линейных неравенств от двух переменных и выяснили, что решением является некоторая область плоскости. Вернемся к задачам линейного программирования. Любая ЗЛП состоит из ограничений, являющихся системой неравенств, и целевой функции.

Определение. Любое решение системы ограничений называется допустимым решением ЗЛП.

Определение. Допустимое решение, в котором целевая функция достигает максимального или минимального значения, называется оптимальным решением.

В силу этих определений задача ЛП может быть сформулирована следующим образом.

Среди всех точек выпуклой области, являющейся решением системы ограничений, выбрать такую, координаты которой минимизируют (максимизируют) линейную функцию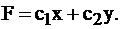

Заметим, что переменные 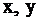в ЗЛП принимают, как правило, неотрицательные значения ( 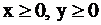), поэтому область расположена в I четверти координатной плоскости.

Рассмотрим линейную функцию 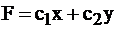и зафиксируем какое-нибудь её значение 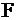, пусть, к примеру 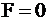: 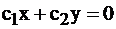. Графиком этого уравнения будет прямая, проходящая через начало координат 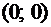, смотри рис.2.5. При изменении этого фиксированного значения 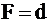прямая 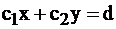будет смещаться параллельно и «зачертит» всю плоскость. Линии 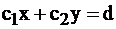являются линиями уровня функции F.

Рис. 2.5

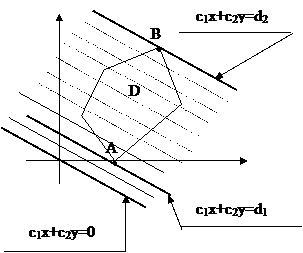Пусть многоугольник 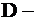допустимая область. При изменении 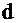прямая 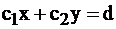при некотором значении 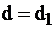достигает многоугольника 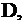назовём эту точку 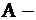«точкой входа», и затем, пройдя многоугольник, при некотором значении 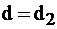будем иметь с ним последнюю общую точку 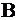, назовём эту точку 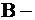«точкой выхода».

Вектор 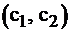является градиентом функции F и показывает направление роста функции.Функция F перпендикулярна этому вектору. Очевидно, что своего наименьшего значения целевая функция 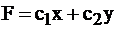достигнет в точке «входа» 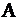и наибольшего значения в точке «выхода» .

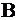Учитывая, что оптимальное значение на множестве допустимых, целевая функция принимает в точке «входа» или «выхода», т. е. в вершинах области решений, можно предложить следующий план решения ЗЛП:

1) построить область решений системы ограничений;

2) построить прямую для целевой функции, перпендикулярную вектору 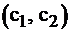, и параллельным переносом этой прямой найти точку «входа» или «выхода» (в зависимости от требования минимизировать или максимизировать целевую функцию);

3) определить координаты этой точки, вычислить в них значение целевой функции.

При графическом решении ЗЛП возможны два особых случая, которые требуют обсуждения.

Случай 1.

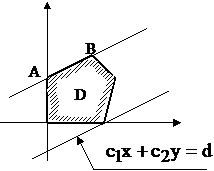При перемещении прямой 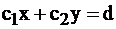«вход» или «выход» произойдет по стороне многоугольника (как на рисунке). Это случится, если в многоугольнике есть стороны, параллельные прямой .

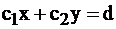В этом случае точек «выхода» («входа») бесконечное множество, а именно любая точка отрезка .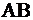

Это означает, что целевая функция принимает максимальное (минимальное) значение не в одной точке, а во всех точках, лежащих на соответствующей стороне многоугольника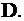

Случай 2.

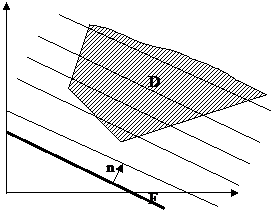Рассмотрим случай, когда область допустимых значений открыта, как в примере 3 § 2.3.

В случае открытой области целевая функция может быть задана таким образом, что соответствующая ей прямая не имеет точки «выхода» (или «входа») из области.

Тогда максимальное (минимальное) значение функции не достигается ни в какой точке, говорят, что функция неограниченно возрастает (убывает).

Рассмотрим графический способ решения на примере задачи 3 (о составлении плана) §2.1, смотри ниже рис.2.5.

Необходимо найти максимальное значение целевой функции 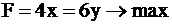при системе ограничений:

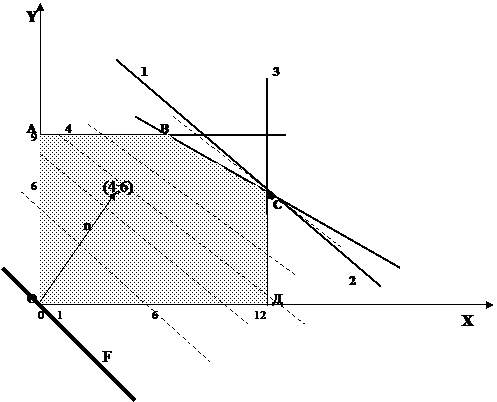
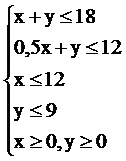
Рис. 2.5 Графическое решение задачи ЛП

1. Построим область допустимых значений, являющуюся решением системы неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами.

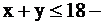полуплоскость ниже прямой 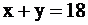(обозначена цифрой 1);

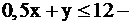полуплоскость ниже прямой 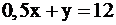(2);

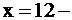прямая, параллельная оси OY (3); 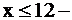полуплоскость левее (3);

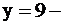параллельна оси OX (4), 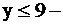полуплоскость ниже ;

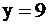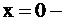ось OY; 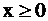– полуплоскость правее оси OY;

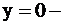ось OX; 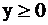– полуплоскость выше оси OX.

2. Пересечением всех этих полуплоскостей является, очевидно, пятиугольник ОАВСД с вершинами в точках О(0;0), А(0;9), В(6;9), С(12;6), Д(12;0). Этот пятиугольник и образует область допустимых значений задачи.

3. Рассмотрим целевую функцию задачи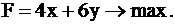

Вектор градиента целевой функции имеет вид 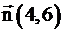. Построим прямую, перпендикулярную этому вектору: 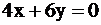. Будем двигать эту прямую параллельным образом. Из всего семейства прямых 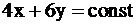последней вершиной, через которую пройдет прямая, при выходе за границу многоугольника, будет вершина 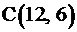. Именно в ней 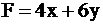достигнет своего максимального значения.

Значит, при 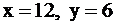функция F достигает своего максимального значения и равна 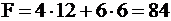. Точка (12; 6) удовлетворяет всем неравенствам системы ограничений, и в ней значение целевой функции оптимально: 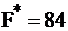(оптимальное значение будем обозначать «*»). Задача решена.

Ответ: необходимо выпустить 12 изделий I вида и 6 изделий II вида, при этом прибыль составит 84 ед.

Еще раз обратим внимание на то, что графический метод применялся нами для решения задач, которые имели в системе ограничений только две переменных. В принципе этот метод может применяться и для систем неравенств, имеющих три переменных. Геометрически ситуация будет иная, более сложная для изображения, роль прямых будут играть плоскости в трехмерном пространстве, а решением неравенства от трех переменных будет являться полупространство, находящееся по одну сторону от плоскости. Роль областей будут играть многогранники, являющиеся пересечением полупространств. Идея метода остается той же.

Каноническая форма задач ЛП

Одним из универсальных методов линейного программирования является симплексный метод, который применим для задач, имеющих каноническую форму.

Определение. Задача ЛП имеет каноническую форму, если:

1) все ограничения системы состоят только из уравнений,

2) переменные неотрицательны,

3) целевую функцию необходимо максимизировать.

Однако в большинстве экономических задач чаще всего в систему ограничений первоначально входят не только уравнения, но и неравенства, как было у нас в задачах 2, 3, 4, 5.

Любая общая задача ЛП может быть приведена к канонической форме. Выполнение первого условия достигается путем введения новых (или их называют дополнительными) переменных. Вернемся к задаче 3. Система ограничений (3) этой задачи состоит из четырех неравенств. Введя дополнительные переменные: 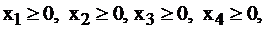можно перейти к системе ограничений:

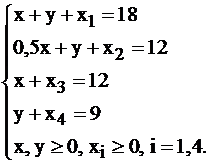(9)

Эти дополнительные переменные 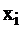имеют конкретный экономический смысл, а именно означают величину неиспользованного времени работы (простоя) машины 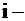го вида. Например, если бы машины первого вида работали все 18 ч., то 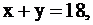следовательно, 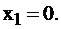Но мы допускаем возможность неполного использования времени работы 1-й машины 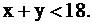В этом случае 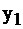приобретает положительное значение и может рассматриваться как неиспользованный лимит времени. Например, зная решение этой задачи из результатов § 2.3, 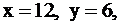мы можем из системы ограничений (9) сделать вывод, что 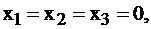а 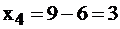. То есть машины 1-го , 2-го, 3-го вида используют свое рабочее время полностью, а вот 4-я машина загружена лишь наполовину: 3 часа при заданном оптимальном плане простаивает. Возможно, после таких выводов руководителю предприятия захочется загрузить ее другой работой, сдать в аренду на это время и т. д.

Итак, введением дополнительных переменных мы можем любое ограничение типа неравенства привести к уравнению.

Рассмотрим задачу о смеси (4 из §2.1). Система ограничений имела вид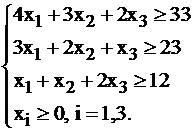

Неравенства были обращены в сторону «больше», поэтому, вводя дополнительные переменные 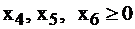их необходимо отнять от левой части, чтобы уравнять ее с правой. Получим систему ограничений в канонической форме:

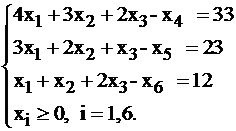
Переменные 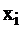также будут иметь экономический смысл. Если вы вспомните практическое содержание задачи, то переменная 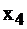будет означать количество излишнего вещества А в смеси, 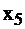– количество излишков вещества В в смеси, 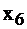– количество излишков С в смеси.

Выполнение второго условия: задача нахождения минимального значения целевой функции может быть сведена к нахождению максимума для функции –F, ввиду очевидности утверждения .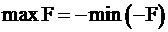

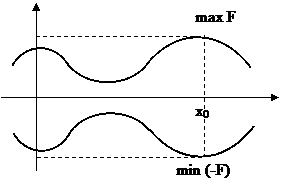Рис. 2.6

Посмотрите на рис. 2.6, если в какой-то точке 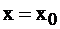функция 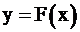достигает своего максимума, то функция 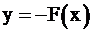, симметричная ей относительно оси OX, в этой же точке 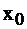достигнет минимума, причем 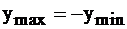при .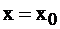

Вып

Выполнение третьего условия – неотрицательности переменных достигается представлением отрицательной переменной в виде разности двух переменных, которые уже в свою очередь неотрицательны: .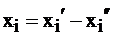

Идея симплексного метода

Симплексный метод является универсальным методом линейного программирования. Его алгоритм состоит из ряда шагов, следуя которым, вы приходите к решению задачи ЛП. Сейчас нас будет интересовать аналитическая идея этого метода, которая при общем взгляде на алгоритм или на «замурованную» программу в ЭВМ не столь ясна, как если бы рассмотреть ее на конкретном примере.

Итак, если мы решаем ЗЛП в канонической форме, то система ограничений – это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений неопределенные, т.е имеющие множество решений.

Например, пусть есть система

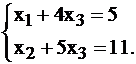
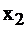Здесь число уравнений равно 2, а неизвестных 3, уравнений меньше ­­– система недоопределена. Выразим и через :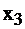

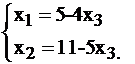
Это общее решение системы. Если переменной 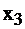придавать любые, произвольные числовые значения, то будем находить частные решения системы. Например, 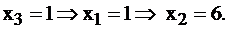Имеем 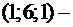частное решение. Пусть 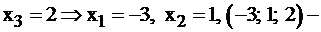другое частное решение. Таких частных решений бесконечно много.

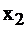Совокупность переменных и образует базис: 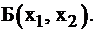Переменные и 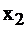называются базисными, а переменная 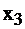– свободной. Если 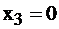, то полученное частное решение (5,11,0) называется базиснымрешением, соответствующим базису