Public static void GetRandValue(int geneIdx)

{

return rand.NextDouble()*

(RightSide[j]-LeftSide[j])+LeftSide[j];

// RightSide[j] – максимальное значение j-го параметра

// LeftSide[j] – минимальное значение j-го параметра

}

}

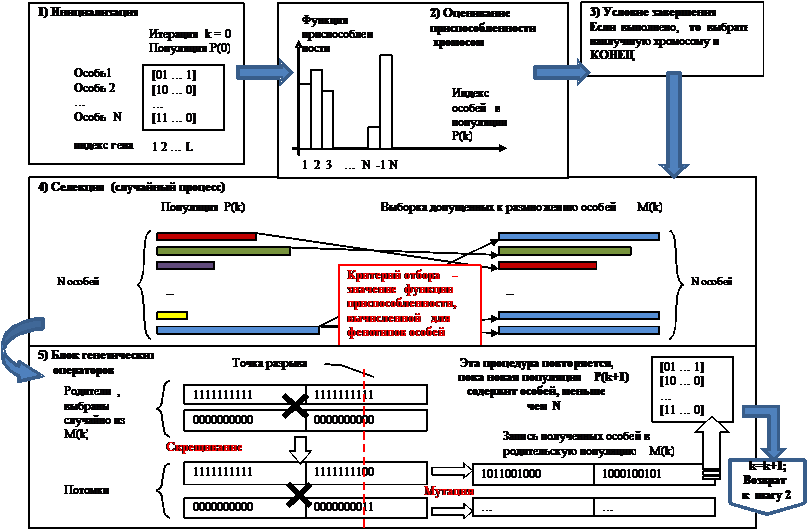
Рисунок 5. Схема выполнения ГА.

2.5.2. Оценивание приспособленности популяции

Оценивание приспособленности хромосом в популяции состоит в расчете функции приспособленности для каждой хромосомы этой популяции. В случае использования целочисленного кодирования для вычисления значения функции приспособленности бывает необходимо преобразовать закодированные в хромосоме целочисленные значения к вещественным числам по формуле (2). Другими словами:

Fitness_i = f(PHENOTYPE_i),

где PHENOTYPE_i = { phen_ik Î R | k = 1,2,...,G } – фенотип (вектор раскодированных параметров) i-й особи, phen_ik – значение k-го гена i-й особи, G – количество генов в хромосоме (параметров в задаче).

Форма функции приспособленности зависит от характера решаемой задачи. Как уже упоминалось, обычно использование ГА используется при решении экстремальной задачи, когда необходимо найти такие значения параметров целевой функции, при которых функция имеет экстремум (оптимум). Таким образом, для задач минимизации считают, что i-я особь приспособленнее k-й особи, если выполняется Fitness_i < Fitness_k. В случае задач максимизации, наоборот, i-я особь приспособленнее k-й особи, если выполняется Fitness_i > Fitness_k.

В результате данного этапа должно быть составлено подобие рейтинга, в котором хранятся значения функции приспособленности для каждой особи текущего поколения и самые приспособленные особи имеют наименьшее значение функции приспособленности.

2.5.3. Проверка условия остановки алгоритма

Определение условия остановки ГА зависит от конкретной задачи. В оптимизационных задачах, если известно максимальное (или минимальное) значение функции приспособленности, то остановка алгоритма может произойти после достижения ожидаемого оптимального значения, возможно - с заданной точностью (малое число, порядка 10^-4÷10^-8 [13]).

Остановка алгоритма также может произойти в случае, когда не происходит видимого улучшения значения некого параметра популяции в течение заданного количества поколений. В этом случае в качестве такого показателя обычно используются [15]:

· средняя приспособленность популяции,

· приспособленность лидера (особи с наилучшей приспособленностью в поколении),

· модуль разницы приспособленностей лидера и наихудшей особи в текущем поколении (так называемый разброс фитнесов популяции),

· расстояние между фенотипами лидера и наихудшей особи в популяции (так называемая длина популяции), которое можно рассчитать как модуль разницы двух векторов-фенотипов указанных особей.

Для подсчета количества итераций, за которые решение не улучшается, в программе обычно декларируется отдельный инкрементный счетчик, который обнуляется в случае улучшения значения параметра. Величину изменения параметра имеет смысл оценивать, опять-таки, с некой заданной точностью. В противном случае ГА может не сойтись.

Очень распространенный и простой критерий остановки – по истечении определенного времени выполнения, либо после выполнения некого предельного количества итераций.

В некоторых источниках [13, 15] реализованные ГА применяют комплекс вышеперечисленных условий. Необходимо подчеркнуть, что каждый критерий остановки необходимо тщательно подбирать и обосновывать применительно к конкретной задаче, а «универсального» подхода здесь, скорее всего, не найти.

Как видно из рис. 4, если условие остановки выполнено, то производится переход к завершающему этапу выбора «наилучшей» хромосомы. В противном случае на следующем шаге выполняется селекция.

2.5.4. Селекция

Селекция хромосом заключается в отборе (по рассчитанным на предыдущем этапе значениям функции приспособленности) тех хромосом, которые будут участвовать в создании потомков для следующей популяции, т.е. для очередного поколения. Такой отбор производится согласно принципу естественного отбора, по которому наибольшие шансы на участие в создании новых особей имеют хромосомы с наибольшими значениями функции приспособленности. Существуют различные методы селекции. Наиболее популярными считаются так называемый метод рулетки (roulette wheel selection), который свое название получил по аналогии с известной азартной игрой и турнирный отбор (tournament selection) [13]. Так как метод рулетки в классическом виде предназначен для максимизации функций и для него характерна чрезмерно быстрая сходимость алгоритма [14], то данное пособие рассматривает только турнирный отбор как более универсальный метод.

Суть турнирного отбора состоит в выборе N наиболее приспособленных особей, где N – размер популяции. Для этого из популяции случайно выбираются t особей, и самая приспособленная из них допускается к скрещиванию (рис. 6.). Говорят, что формируется турнир из t особей, где t – размер турнира. Эта операция повторяется N раз, что в итоге формирует некую промежуточную выборку из N особей, средняя приспособленность которых не хуже, чем средняя приспособленность всех особей текущего поколения.

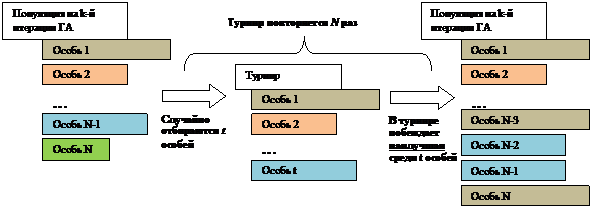
Рисунок 6. Иллюстрация турнирного отбора.

Чем больше значение t, тем больше «давление» селекции на популяцию, и тем быстрее сойдется алгоритм. Вариант турнирного отбора, когда t = 2, называют бинарным турниром. Типичные значения размера турнира t = { 2, 3, 4, 5 }.

Таким образом, селекция приводит к формированию из текущего поколения некой промежуточной выборки из N особей (так называемого родительского пула [13]), которые допущены к размножению.

2.5.5. Генетические операторы

В классическом ГА применяются два основных генетических оператора: оператор скрещивания (crossover) и оператор мутации (mutation). Однако стоит отметить, что оператор мутации играет лишь корректирующую роль по отношению к оператору скрещивания. Скрещивание в классическом ГА производится практически всегда, тогда как мутация - достаточно редко [13]. Вероятность скрещивания, как правило, достаточно велика (обычно 0,5 £ p_c £ 1), тогда как вероятность мутации устанавливается весьма малой (чаще всего 0 < р_m £ 0,1). Это следует из аналогии с миром живых организмов, где мутации происходят чрезвычайно редко.

2.5.5.1. Оператор скрещивания. Отобранные в результате селекции особи (называемые родительскими) скрещиваются и дают потомство. Хромосомы потомков формируются в результате обмена генами между родительскими особями (оператор скрещивания, или, как говорят, кроссовер). Созданные таким образом потомки составляют популяцию следующего поколения. Ниже приведены основные виды скрещивания для целочисленного и вещественного кодирования.

Механизм работы данного оператора выглядит так: из родительского пула случайным образом выбираются 2 особи и скрещиваются с вероятностью p_c, в результате чего создаются 2 потомка. Этот процесс повторяется до тех пор, пока не будет создано N потомков. Вероятность скрещивания p_c является одним из ключевых параметров ГА и в большинстве случаев ее значение лежит в интервале от 0,6 до 1. Внешняя программная реализация кроссовера на псевдоязыке может выглядеть следующим образом:

k = 0;

ПОКА (k < РАЗМЕР_ПОПУЛЯЦИИ)

{

i = RANDOM * РАЗМЕР_ПОПУЛЯЦИИ;

j = RANDOM * РАЗМЕР_ПОПУЛЯЦИИ;

ЕСЛИ (Pc > RANDOM)

{

СКРЕЩИВАНИЕ(РОДИТЕЛЬСКИЙ_ПУЛ[i], РОДИТЕЛЬСКИЙ_ПУЛ[j], OUT СЛЕДУЮЩЕЕ_ПОКОЛЕНИЕ[k], OUT СЛЕДУЮЩЕЕ_ПОКОЛЕНИЕ[k+1]); //*

k = k+2;

}

}

где размер родительского пула равен размеру популяции N; RANDOM – случайная величина, равномерно распределенная на интервале [0; 1]; OUT – ключевое слово, по аналогии с языком C# означающее, что переменная, которая указана после него, служит для возврата результирующего значения из функции. Таким образом, строка, помеченная символом ‘*’, означает, что на вход конкретного оператора скрещивания передаются случайно выбранные особи из структуры родительского пула, а на выходе возвращаются особи-потомки, которые последовательно записываются в некую промежуточную структуру потомков. Забегая вперед, также необходимо помнить о том, что для каждой выбранной пары родителей кроссовер и мутация применяются в связке с вероятностями p_c и p_m соответственно. В случае, когда кроссовер не выполняется (вероятность 1-p_c), пара особей-родителей сразу же помещается в следующее поколение, минуя мутацию. Инверсия же применяется с вероятностью p_I к каждой особи следующего поколения, независимо от того, выполнялся ли кроссовер. Логику этого процесса можно проследить на рис. 7.

Целочисленное кодирование. Для целочисленного кодирования часто используются 1-точечный, 2-точечный и однородный операторы скрещивания. 1-точечное скрещивание работает следующим образом: выбирается произвольная точка разрыва и для создания потомков производится обмен частями родительских хромосом. Иллюстративный пример работы 1-точечного скрещивания представлен на рис. 8

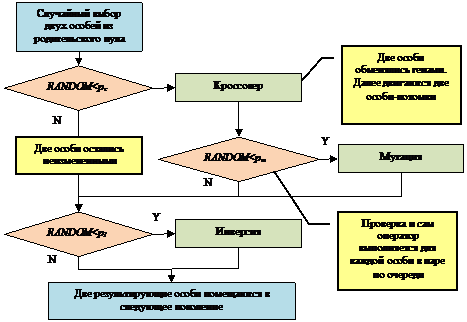
Рисунок 7. Диаграмма процесса размножения особей в ГА.

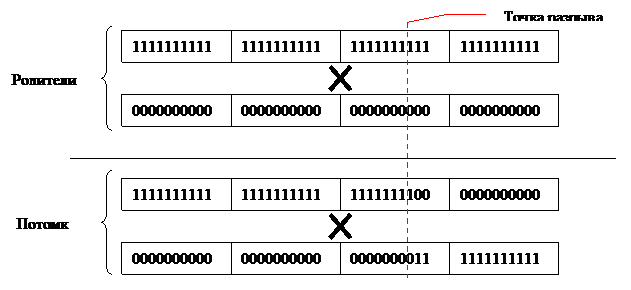
Рисунок 8. Пример работы 1-точечного скрещивания

Для оператора 2-точечного скрещивания выбираются 2 случайные точки разрыва, после чего для создания потомков родительские хромосомы обмениваются участками, лежащими между точками разрыва. При использовании однородного оператора скрещивания разряды родительских хромосом наследуется независимо друг от друга. Для этого определяют вероятность p₀, что i-й разряд хромосомы первого родителя попадет к первому потомку, а второго родителя – ко второму потомку. Вероятность противоположного события равна (1 – p₀). В большинстве случаев вероятность обоих событий одинакова, т.е. p₀ = 0,5.

Вещественное кодирование. Для вещественного кодирования рассмотрим 2-точечный, арифметический и BLX-a операторы скрещивания. 2-точечное скрещивание для вещественного кодирования, в целом, аналогично 2-точечному скрещиванию для целочисленного кодирования. Различие заключается в том, что точка разрыва не может быть выбрана «внутри» гена, а должна лежать на границе между генами (см. рис. 9).

Рисунок 9. Пример работы 2-точечного скрещивания для вещественного кодирования

При использовании арифметического и BLX-a операторов процесс обмена генов между родительскими особями зависит от значений генотипов родителей. Обозначим g_k⁽¹⁾ g_k⁽²⁾ – k-е гены родительских особей, 1 ≤ k ≤ L, L – количество генов в хромосоме. Пусть также h_k⁽¹⁾ и h_k⁽²⁾ – k-е гены потомков. Тогда для арифметического скрещивания:

,

,

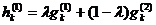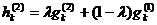где 0 ≤ l ≤ 1.

Если используется BLX-a скрещивание, то значение k-го гена потомка выбирается случайным образом (обычно с равномерным распределением) из интервала [c_min – a × D_k, c_max + a × D_k], где a – константа,

c_min = min{g_k⁽¹⁾ g_k⁽²⁾},

c_max = max{g_k⁽¹⁾ g_k⁽²⁾},

D_k = c_max - c_min.

Изображение интервала, используемого для BLX-a скрещивания показано на рис. 10.

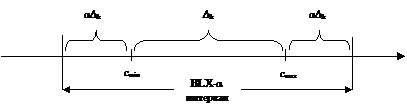
Рисунок 10. Интервал для BLX-a скрещивания

Разрушающая способность скрещивания. Операторы скрещивания характеризуются способностью к разрушению (disruption ability) родительских хромосом. Скрещивание для целочисленного кодирования считается тем разрушительнее, чем больше в результате его применения расстояние по Хэммингу между получившимися хромосомами потомков и родителей. Расстояние Хэмминга – это число разрядов, в которых цифры сравниваемых двоичных слов одинаковой длины различны[4]. Другими словами, способность целочисленного скрещивания к разрушению зависит от того, насколько сильно он «перемешивает» содержимое родительских хромосом. Так, одноточечное скрещивание считается слаборазрушающим, а однородное скрещивание в большинстве случаев является сильноразрушающим оператором. Двухточечное скрещивание по разрушающей способности занимает промежуточную позицию по отношению к одноточечному и однородному операторам. Для скрещивания при вещественном кодировании способность к разрушению определяется тем, насколько велико расстояние по Евклиду в пространстве поиска между точками, соответствующими хромосомам родителей и потомков. Таким образом, разрушающий эффект 2-точечного скрещивания зависит от содержимого родительских хромосом. Разрушающая способность арифметического скрещивания зависит от значения параметра l, например, при l ® 1 и l ® 0, способность к разрушению будет низкой. Для BLX-a скрещивания разрушающая способность зависит как от значения a, так и от разности значений соответствующих генов родительских особей. Разрушая хромосомы родительских особей, скрещивание может создать новые решения, не встречавшиеся ранее в процессе поиска.

2.5.5.2. Оператор мутации. Сразу после скрещивания на потомках применяется мутация, которая предназначена для внесения случайных изменений в хромосомы особей. Это позволяет алгоритму «выбираться» из локальных экстремумов и, тем самым, эффективнее охватывать пространство поиска. Так же, как и для оператора скрещивания, имеет смысл определить вероятность применения мутации p_m. Далее приведены различные операторы мутации в зависимости от способа кодирования генетической информации.

Целочисленное кодирование. В случае целочисленного кодирования мутация изменяет отдельные разряды в хромосоме. Для этого каждый разряд инвертируется с вероятностью p_m. Ниже приведен пример мутации на псевдокоде: