Нахождение оригинала по изображению

При расчете переходных процессов операторным методом необходимо не только находить изображение функций, их производных и интегралов, но и решать обратную задачу – находить функции (оригиналы) по их изображениям. Существуют следующие способы решения этой проблемы:

1. Использование обратного преобразования Лапласа

, (4.35)

которое представляет собой решение интегрального уравнения (4.27) относительно неизвестной функции f(t) и может быть получено методами теории функций комплексного переменного. Интеграл (4.35) вычисляется по прямой на плоскости комплексного переменного p, параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F(p). Такой способ в прикладных задачах электротехники не используется.

2. Табличный метод. Подробные таблицы оригиналов и соответствующих им изображений приводятся в математических и электротехнических справочниках. При использовании этого способа возникают трудности, связанные с распознаванием и сведением функций к табличному виду.

3. Использование теоремы о вычетах или теоремы разложения.

Для каждой функции времени, входящей в уравнение Кирхгофа, описывающего расчетную цепь, устанавливается в соответствие операторное изображение, после чего система линейных дифференциальных уравнений переписывается в виде системы алгебраических уравнений (также получаем операторную схему замещения). Система алгебраических уравнений рассчитывается относительно операторного изображения искомой величины, по которому с помощью теоремы разложения находится оригинал.

Теорема разложения имеет две модификации в зависимости от операторного изображения искомой величины:

1) 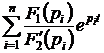_·=^· , (4.31)

где n – порядок цепи,

p_i – простые корни характеристического уравнения N(p) = 0;

.

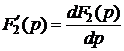2) 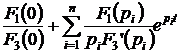_·=^· , (4.32)

где p_i – корни характеристического уравнения F₃(p) = 0.

В этом случае знаменатель имеет один нулевой корень, на это указывает наличие в составе знаменателя множителя p. Теорема разложения в форме (4.32) соответствует сигналам, имеющим принужденную составляющую.

Если уравнение F₂(p) = 0 имеет комплексные сопряженные корн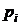и и 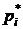, то достаточно вычислить слагаемое сумм (4.31) или (4.32) только для корня 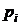, а для корня 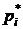взять значение, сопряженное этому слагаемому, т.е.

_·=^· (4.33)

или

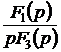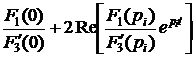_·=^· . (4.34)

Если среди корней многочлена F₂(p) = 0 есть q простых корней (p₁, p₂, …, p_q), корень p_r кратности r и корень p_s кратности s, то можно записать теорему разложения с двойной суммой в правой части (одна сумма – по числу корней, а вторая – для каждого корня по порядку его кратности):

_·=^·

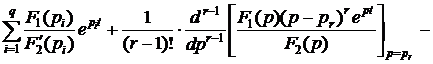
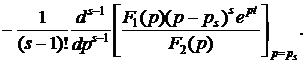(4.35)

Если нужно вычислить начальное (при t = 0⁺) и установившееся (при t = ¥) значения оригинала, т.е. f(0⁺) и f(¥), то можно воспользоваться формулами (4.31) и (4.32). Однако начальное и установившееся значения оригинала в случае, если установившийся процесс непериодический, определяются достаточно просто по так называемым предельным соотношениям:

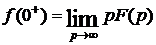(4.36)

и

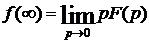. (4.37)

Рассмотрим специфические особенности применения метода.

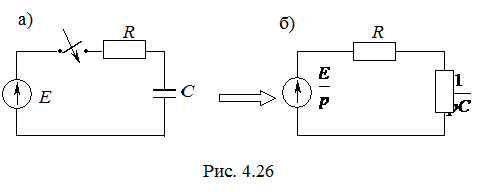
Пример 1. Рассмотрим заряд конденсатора при подключении RC–цепи на постоянное напряжение (рис. 4.26, а). Определим закон изменения в переходном режиме.

Цепь с нулевыми начальными условиями. Соответствующая операторная схема замещения представлена на рис. 4.26, б.

Операторное изображение напряжения на конденсаторе определим по закону Ома:

Изображение тока в операторной схеме замещения

Для отыскания воспользуемся теоремой разложения: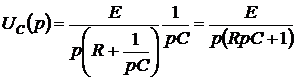

_·=^· .

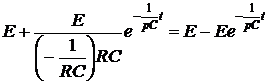Используя предельные соотношения, определим соответственно начальное и установившееся значения напряжения на конденсаторе:

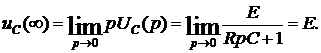
Аналогичные значения будут получены по формуле, описывающей закон изменения 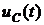в переходном режиме

и

.

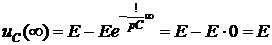Пример 2. Найти напряжение на емкости в цепи (рис. 4.27), подключенной к источнику постоянного напряжения U = 4 B. Параметры элементов электрической цепи приведены на рисунке.

1. Анализ независимых начальных условий (докоммутационный режим)

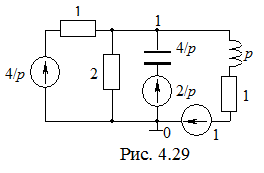2. Эквивалентная операторная схема представлена на рис. 4.29.

Операторные сопротивления:

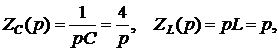
Операторные ЭДС:

3. Расчет эквивалентной операторной схемы методом узловых потенциалов:

.

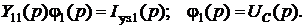
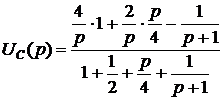После необходимых преобразований получим

.

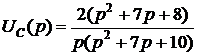4. Для отыскания 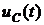воспользуемся теоремой разложения:

_·=^· ,

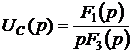здесь ,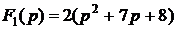

,

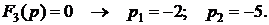
Таким образом,

.

Окончательно

.
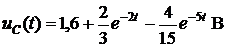