Свойства математического ожидания.
1. Математическое ожидание неслучайной величины с равно самой величине с:
M[c] = c. (6.4)
Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1:
M[c]=c∙1=c.
2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание:
M[c×X] = c×M[X]. (6.5)
Доказательство:
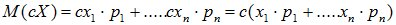
3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:
 (6.6)
(6.6)
Доказательство: следует из свойств 1 и 3.

4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M[X+Y] = M[X]+M[Y]. (6.6)
10.Числовые характеристики случайных величин. Дисперсия. Свойства дисперсии.
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.
Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.
Расчетные формулы:
 (6.9)
(6.9)
Дисперсия может быть вычислена через второй начальный момент:
 (6.10)
(6.10)
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.
Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.
11.Средним квадратическим отклонением (СКО) СВ X называется характеристика 
 . (6.11)
. (6.11)
СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.
Свойства дисперсии
Дисперсия постоянной величины с равна нулю.
Доказательство: по определению дисперсии
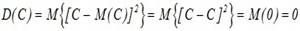
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.
D[X+c] = D[X].
Доказательство: по определению дисперсии
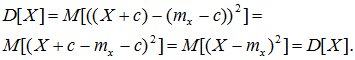 (6.12)
(6.12)
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.
Доказательство: по определению дисперсии
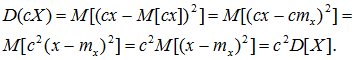 . (6.13)
. (6.13)
Для среднего квадратичного отклонения это свойство имеет вид:
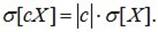 (6.14)
(6.14)
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. 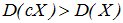 . Если 0<½с½<1, то
. Если 0<½с½<1, то 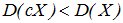 .
.
Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:
[ m - 3s; m + 3s; ].(6.15)
12. Распределения дискретных случайных величин. Биномиальное, Пуассона, геометрическое, гипергеометрическое распределения.
Исходной информацией для построения функции распределения дискретной случайной величины X является ряд распределения этой СВ.
| xi | x1 | x2 | x3 | ... | xn | >xn |
| pi | p1 | p2 | p3 | ... | pn | |
| F(xi) | p1 | p1+p2 | … | p1+..+pn-1 |
F(xi)=P{X<xi}=P{(X=x1)È(X=x2)È ... È(X=xi-1)}= p1+...+pi-1.
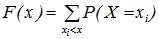 , то есть суммирование распространяется на все значения
, то есть суммирование распространяется на все значения 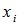 , которые меньше х.
, которые меньше х.
Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятности этих значений.
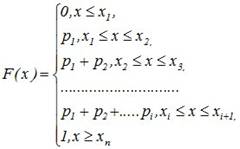
Биномиальное распределение.
Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли:
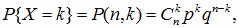
где p – параметр распределения 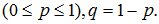
Распределение загасит от двух параметров п и р.
На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Числовые характеристики: М [Х] = n, D[X]= npq.
Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
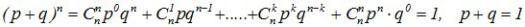 ,
,
т.е. 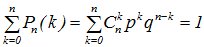
Распределение Пуассона.
Соотношениями, описывающими биноминальное распределение, удобно пользоваться в тех случаях, если величина и достаточно мала, а р велико.
Теорема: Если, 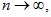 а
а 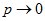 так, что
так, что 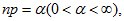 то
то
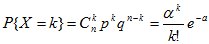
при любом k=0,1,….
Числовые характеристики: М[Х] = α, D[X] = α.
Закон Пуассона зависит от одного параметра α, смысл которого заключается в следующем: он является одновременно и математическим ожиданием и дисперсией случайной величины Х.
