Минимально необходимый объем выборки

для нахождения непараметрических толерантных пределов при Р = 0.95

Q	0.8	0.9	0.95	0.99	k
n
n
n
n

За независимость от вида плотности распределения исследуемой генеральной совокупности приходится “платить” существенным увеличением объема выборки (см. табл. 4). Кроме того, становится ясно, почему в качестве толерантных пределов выбираются члены вариационного ряда, расположенные поближе к его краям.

Ранее подробно был рассмотрен случай нахождения непараметрических толерантных пределов для интервального оценивания интерквантильного промежутка 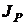, симметричного относительно математического ожидания (см. разд. 1.6.2, рис. 10, а).

В ряде случаев, когда математическое ожидание случайной величины невелико по сравнению с ее среднеквадратическим значением, объем выборки может быть уменьшен без ущерба для достоверности оценок. Как правило, такая ситуация встречается при экспериментальном определении характеристик погрешности средств измерений или результатов измерений, или характеристик точности регуляторов, позиционеров, систем автоматического управления и регулирования, когда в составе погрешности этих устройств имеются и случайные, и систематические составляющие, но в документации на эти средства установлены нормы на сумму этих составляющих. Пример такого интерквантильного промежутка приведен в разд. 1.6.2 (см. на рис. 10, б). Он обозначен там 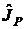и имеет границы [–g, g]. В подобных случаях рекомендуется поступать следующим образом.

Исходная выборка значений погрешностей 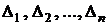, среди которых имеются положительные и отрицательные значения, преобразуется в выборку, состоящую из абсолютных величин этих исходных значений. В результате весь вариационный ряд оказывается на правой полуоси, что снимает заботу об отбрасывании первого статистически эквивалентного блока, а именно, 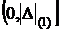, поскольку обе границы доверительного интервала для интерквантильного промежутка, симметричного относительно начала координат, определяются конечными членами вариационного ряда, составленного из модулей выборочных значений .

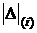В этом случае толерантные пределы 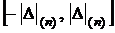, составленные на основе одного лишь максимального члена этого вариационного ряда, являются границами доверительного интервала для интерквантильного промежутка 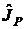(см. разд. 1.6.2, рис.10, б), если, конечно, объем выборки достаточен для этого. Поскольку в этом конкретном случае не отбрасывается ни один статистически эквивалентный блок (ибо первый, как уже было сказано, нас не интересует, а последним блоком является 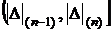), минимально необходимый объем выборки находят при k = 0 из неравенства

.

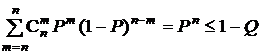Этому варианту соответствует первая строчка в табл. 4.

Понятно, что при желании застраховаться от вредного влияния грубых промахов или помех количество отбрасываемых членов может быть увеличено в два раза при том же объеме выборки. При этом доверительная вероятность не изменится, а объем выборки, необходимый при отбрасывании одного, двух и более крайних членов, находится из последующих строк данной таблицы. Видно, что достигается существенная экономия объема выборки. “Платой” за это является расширение доверительного интервала.

Бутстреп – оценивание

Бутстреп[1]-оценивание – метод нахождения доверительных интервалов для числовых характеристик случайных величин и любых параметров плотности распределения, не зависящий от вида плотности распределения генеральной совокупности из которой извлечена выборка. Этот метод предложен Б. Эфроном и описан в его книге [10] а также в серии статей отечественных авторов, опубликованных в журнале [11].

Метод заключается в следующем.

Пусть имеется выборка 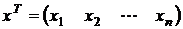, извлеченная из генеральной совокупности X, плотность распределения которой 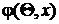, где Q – числовая характеристика или параметр, для которого по этой выборке –необходимо определить границы доверительного интервала.

Согласно бутстреп-методу, из имеющейся выборки конструируются бутстреп-выборки путем комбинации исходных выборочных значений при условии, что бутстреп-выборки должны отличаться хотя бы одним элементом. Порядок расположения элементов бутстреп-выборок не имеет значения. Объем бутстреп-выборок может быть различным, но, по построению, он будет обязательно меньше n. По каждой из бутстреп-выборок вычисляется оценка числовой характеристики или параметра Q.

Обозначим бутстреп-выборки 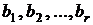, объемы этих выборок – 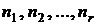, оценки параметра – 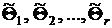. Объединим все эти обозначения в табл. 5.

Из полученных оценок строится вариационный ряд

,

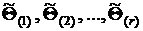и задача определения границ доверительного интервала для параметра Qпри доверительной вероятности Q ставится, как задача оценки интерквантильного промежутка 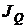с помощью непараметрических толерантных пределов (см. разд. 2.4.6.2.), если, конечно, количество членов вариационного ряда достаточно для этого. Поскольку в этой процедуре не могут возникать грубые промахи и резкие выбросы значений оценок 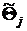, здесь не имеет смысла страховаться от них, поэтому достаточно использовать

Таблица 5

Бутстреп-выборки и оценки

Обозначение выборки	Бутстреп- выборка	Объем выборки	Оценка числовой характеристики (параметра)

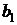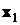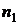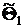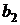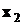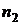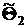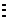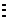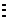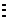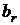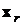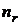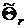только крайние члены вариационного ряда, то есть только первую строчку табл. 4 ( при оценивании интервала с симметричными границами) или вторую строчку (при оценивании правой и левой границы по отдельности). В качестве доверительной вероятности в данной ситуации принимается вероятность p из интервала значений (0.8 – 0.9), которая в дальнейшем не фигурирует, как характеристика качества оценки параметра Q.

Таким образом, для реализации бутстреп-метода оценивания используются непараметрические толерантные пределы из п. 2.4.6.2. применительно к вариационному ряду 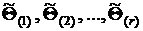со следующей заменой: вероятность P (см. п.. 2.4.6.2). заменяется на вероятность Q настоящего пункта, в качестве вероятности Q (см. п. 2.4.6.2) назначается вероятность p. Доверительной вероятностью для найденного доверительного интервала параметра считается вероятность Q.

На первый взгляд, метод кажется некорректным.

По теореме Шеннона, никакое преобразование информации не приводит к увеличению ее количества (эта теорема логически согласуется с положением физики о невозможности создания вечного двигателя). В данном случае, когда для нахождения доверительного интервала требуется значительное количество информации (как мы убедились хотя бы в предыдущем пункте), здесь она как будто добывается путем простого комбинирования элементов исходной выборки, информации в которой до того было недостаточно для решения той же задачи. И здесь не в пользу бутстреп-метода, но в согласии с английским бытовым значением этого слова возникают ассоциации с «опытом» барона Карла Иеронима Фридриха фон Мюнхгаузена самовынимания себя вместе с лошадью из болота за собственный парик.

Серьезные сомнения в корректности этого метода широко распространены в среде математиков – специалистов в области теории вероятностей и математической статистики.

Тем не менее публикации практических результатов применения этого метода и результаты статистического моделирования свидетельствуют о работоспособности метода в определенных условиях.