Доверительный интервал для вероятности

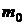Оценивается вероятность p события A по результатам n независимых испытаний, исходами которых может быть одно из двух событий A и . Пусть - количество появления события A в n испытаниях. Точечной оценкой вероятности в соответствии с частотным определением (см.разд. 1.2.2) является отношение

.

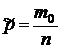Эти испытания соответствуют схеме Бернулли (см. разд. 1.2.4), в соответствии с которой вероятность того, что событие A появилось 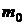раз

.

Требуется найти нижнюю и верхнюю 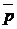границы интервала, который накрывает истинное значение вероятности pс вероятностью Q.

Начнем с поиска нижней границы на примере.

Пусть было выполнено n = 100 испытаний и событие A осуществилось 50 раз.

Предположим, что =0.Но это предположение не подтверждается полученным результатом, ибо при такой вероятности событие A не должно осуществиться никогда, как невозможное событие, а оно осуществилось и неоднократно.

Предположим, что 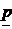=0,01.Воспользуемся формулой для 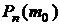и расcчитаем вероятность того, что при 100 испытаниях событие A осуществится 50 раз. Эта вероятность равна примерно 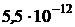. Она настолько мала, что и в этом случае мы не можем заключить о подтверждении нашего предположения результатом испытаний

Это же заключение можно сформулировать иначе: “При вероятности события A,равной 0,01, полученный результат практически невозможен, а потому это предположение не может считаться достаточно обоснованным”.

Предположим, что =0,1. В этом случае вероятность того, что при 100 испытаниях событие A осуществится 50 раз, должна была бы быть равна примерно 0,014. Это весьма незначительная вероятность, и поэтому и в данной ситуации мы не можем считать, что наше предположение подтверждается экспериментально.

Предположим, что =0,2. В этом случае . Такая вероятность полученного исхода нашего испытания может считаться достаточной для того, чтобы считать этот исход возможным. Если это так, и такая вероятность представляется исследователю удовлетворительной, он принимает значение р = 0,2 в качестве нижней границы доверительного интервала.

На этом примере мы видим, что с увеличением предполагаемого истинного значения вероятности p значение вероятности 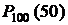монотонно возрастает, и в этом конкретном примере нижняя граница доверительного интервала для вероятности находится из уравнения

,

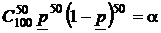где a – заданное значение вероятности, достаточное для того, чтобы считать полученный исход вполне возможным.

Однако, из материалов разд. 1.2.4 следует, что вероятность 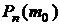в схеме Бернулли имеет максимум в окрестности значений, связанных равенством m = np. Это означает, что приведенное уравнение имеет два решения, из которых для определения нижней границы следует выбрать только одно, удовлетворяющее условиюp < m/n. Чтобы избавиться от этой двузначности и обеспечить дополнительные гарантии, принято находить нижнюю границу доверительного интервала для вероятности в схеме Бернулли из уравнения

.

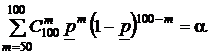В этом уравнении левая часть монотонно зависит от , и тем самым имеет только одно решение. Решение этого уравнения имеет следующий смысл: в качестве нижней границы доверительного интервала для вероятности выбирается такое значение, при котором вероятность появления события A не менее 50 раз достаточна для того, чтобы считать полученный исход испытания вполне возможным.

В общем случае для нахождения нижней границы доверительного интервала для вероятности используется неравенство

.

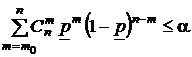На том же примере рассмотрим подход к определению верхней границы доверительного интервала для вероятности в схеме Бернулли.

Предположим, что = 1.Это предположение не подтверждается результатом выполненного испытания, поскольку в этих условиях событие A должно осуществиться 100 раз, а полученный результат 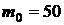невозможен, вероятность его осуществления равна нулю.

Предположим теперь, что =0,7.Если это было бы так на самом деле, то вероятность полученного результата была бы равна 0,0000064, то есть этот результат маловероятен, и говорить о том, что результат испытаний подтверждает наше предположение, мы вряд ли можем.

Точно так же, как это было при отыскании нижней границы доверительного интервала, мы в конце концов найдем такое значение >m/n, при котором вероятность 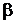осуществления полученного нами результата окажется достаточной для того, чтобы считать это предположение оправданным:

.

И в этом случае из тех же соображений, что и ранее, верхняя граница доверительного интервала для вероятности отыскивается из неравенства

.

Мы построили доверительный интервал для вероятности с границами , такой, что

,

с доверительной вероятностью .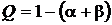

Обычно принимают a = b, и Q = 1 – 2a.