Оценивание коэффициентов аппроксимирующих полиномов

2.3.7.1. Формулировка задачи

Будем рассматривать следующую ситуацию. Объективно существует функция y = f(x), ограниченная и дифференцируемая не менее q + 1 раз на интервале 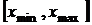. Природа и происхождение этой функции могут быть различными:

этой функцией связаны между собой естественные параметры и(или) явления в природе, в обществе, в экономике и т.п.;

этой функцией описывается преобразование физических величин, происходящее в технических устройствах, таких, как регуляторы, датчики, измерительные преобразователи, устройства телекоммуникаций и т.п.;

этой функцией описываются взаимосвязи параметров технических объектов, в том числе технологических процессов, в различных режимах (штатный режим работы, испытания, нештатные режимы);

этой функцией, по мнению исследователя, описываются объекты, явления, процессы, которые он моделирует на компьютере.

По теореме Вейерштрасса, ограниченные и q +1 раз дифференцируемые в интервале 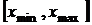функции могут быть сколь угодно точно аппроксимированы в этом интервале степенным (и даже обобщенным) полиномом.

Понятно, что в реальном исследовании сколь угодно высокая точность достигнута быть не может, хотя стремление к максимально достижимой точности у каждого исследователя имеется. Пусть это естественное стремление выражается следующим образом.

Желательно аппроксимировать реальную функцию y = f(x)полино­мом степени q так, чтобы максимальное расхождение между реальной функцией и этим полиномом не превосходило пренебрежимо малой, с точки зрения исследователя, величины d > 0 :

.

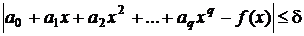Будем называть этот полином степени q “точным”.

Поскольку, по теореме Вейерштрасса, такой полином существует при любом сколь угодно малом значении δ,будем считать коэффициенты 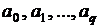“истинными” и для их обозначения введем вектор этих коэффициентов 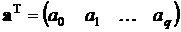. Степень полинома q будем считать известной. В этом случае говорят: “модель объекта известна с точностью до параметров”. Объектом для нас является полином, аппроксимирующий функцию y = f(x).

Теперь задачей исследователя является организация такого экспе­римента, в результате которого он смог бы определить значения этих коэффициентов. Необходимыми условиями выполнения такого эксперимента являются

воспроизведение с необходимой точностью заданных значений аргумента 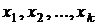, , 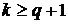в диапазоне 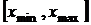, или, по крайней мере, фиксация фактически реализующихся этих значений с помощью измерений с заданной или хотя бы с известной точностью;

измерение с необходимой или хотя бы с известной точностью значений функции 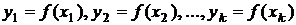при всех заданных (зафиксированных) значениях аргумента.

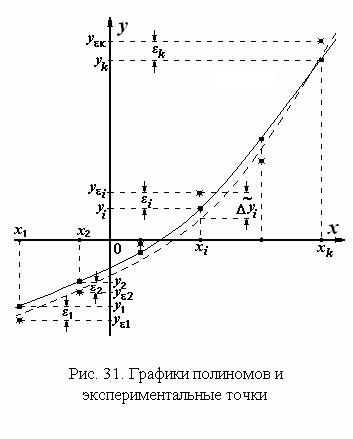
Пример графического представления результатов подобного эксперимента приведен на рис. 31. Непрерывной кривой изображен график исследуемой функции y = f(x), точки на этой кривой – суть значения

.

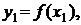
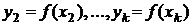Для обозначения всей совокупности этих значений введем вектор 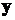: 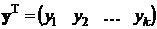. Точки вне этой кривой – результаты измерений, для обозначения которых введем вектор : .

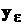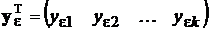Будем считать, что воспроизведение (измерения) значений аргумента выполняются с настолько высокой точностью, что погрешностью результатов можно пренебречь.

Будем также считать, что погрешности 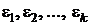измерения значений функции суть компоненты случайного вектора ε, не содержащие систематических составляющих (математическое ожидание всех компонент равно нулю), вектор ε распределен в соответствии с нормальным законом: 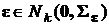, где 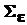– его ковариационная матрица. Диагональными элементами ковариационной матрицы 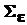являются дисперсии погрешностей измерений 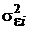. Результаты измерений образуют в совокупности случайный вектор 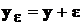, который распределен нормально 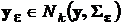. В случае независимости измерений ковариационная матрица 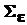диагональна.

Задача состоит в том, чтобы выполнить полиномиальную аппроксимацию исследуемой функции y = f(x), то есть найти оценки коэффициентов 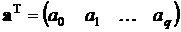полинома, аппроксимирующего эту функцию.

Измерения значений функции при каждом значении аргумента могут быть однократными или многократными.

Рассмотрим вначале случай однократных измерений, которым можно ограничиться только, если ковариационная матрица 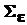известна априори.

2.3.7.2. Измерения однократные

В соответствии с формулировкой задачи (разд. 2.3.7.1) в результате эксперимента при фиксированных значениях 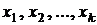мы получаем значения , :

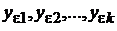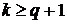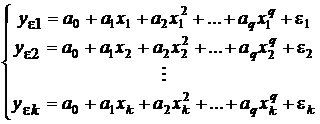
Эти значения представлены точками (см. рис. 31), лежащими вне кривых.

Приведенная система равенств есть система k уравнений, из которой нам необходимо получить оценки q + 1 коэффициентов .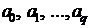

Для того чтобы эту систему записать в матричном виде, введем матрицу

.

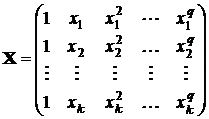Тогда система уравнений записывается в виде

,

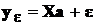где векторы 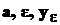определены в п. 2.3.7.1 и

, .

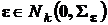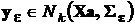Будем находить ММП-оценки неизвестных коэффициентов полинома. Для этого запишем k-мерную плотность распределения вектора :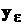

.

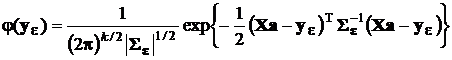Функция правдоподобия в этом случае

.

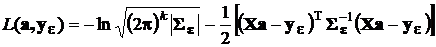Максимум функции правдоподобия находится там же, где находится минимум квадратичной формы :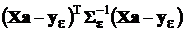

,

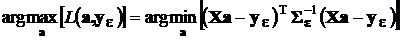поэтому для нахождения ММП-оценок искомых коэффициентов будем их отыскивать путем минимизации указанной квадратичной формы. С этой целью продифференцируем ее по вектору а и приравняем производную нулю. Напомним предварительно правила дифференцирования по вектору (см., например, [5], стр. 73):

.

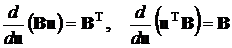Пользуясь этими правилами после раскрытия скобок, получим

,

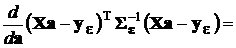
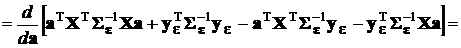
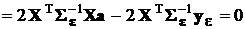откуда находим вектор ММП-оценок коэффициентов аппроксимирующего полинома:

,

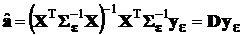где .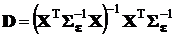

Очевидно, что эта оценка линейно зависит от результатов измерений, а размер матрицы D равен (q + 1) k.

Являясь ММП-оценкой, полученный вектор есть эффективная оценка вектора коэффициентов полинома. Проверим ее несмещенность:

,

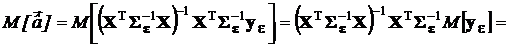
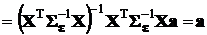поскольку произведение взаимно обратных матриц есть единичная матрица. Несмещенность полученной оценки доказана.

Как показано в разд.3.7.1, ковариационная матрица вектора 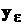есть 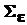. Тогда, поскольку 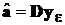, то в соответствии с разд. 1.7.4 ковариационная матрица вектора оценок коэффициентов

.

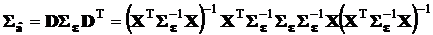Производя перемножение ряда взаимно обратных матриц, находящихся в середине правой части, окончательно получим:

.

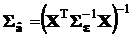Напомним также, что при линейном преобразовании случайных величин вид плотности распределения не изменяется (разд. 1.6.7). Поэтому в связи с обнаруженной нами несмещенностью оценки

.

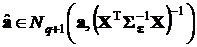Если измерения равноточные, то есть при всех i = 1, 2, ..., k 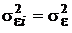, а компоненты вектора ε независимы, то ковариационная матрица 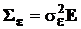, где Е – единичная матрица, 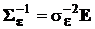. В этих условиях квадратичная форма, подлежащая минимизации, принимает вид

.

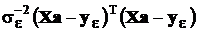В результате минимизации получаем решение и его характеристики

.

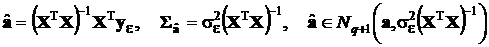Компонентами вектора 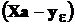являются разности

,

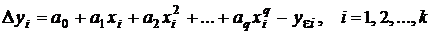и минимизируемая квадратичная форма представляет собой сумму квадратов этих разностей:

.

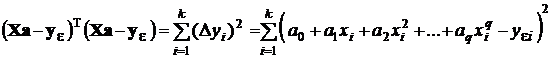По этой причине приведенный метод определения коэффициентов аппроксимирующих полиномов называется методом наименьших квадратов (МНК), а получаемые этим методом оценки коэффициентов полиномов называются МНК-оценками.

Общий метод оценивания коэффициентов аппроксимирующих полиномов путем минимизации квадратичной формы 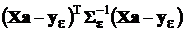называется обобщенным методом наименьших квадратов (ОМНК), а оценки, вычисляемые по формуле 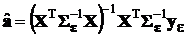, – ОМНК‑оцен-ками.

Конечным итогом и целью оценивания является полином, коэффициентами которого являются найденные оценки:

.

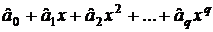При значениях аргумента 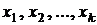этот полином принимает значения, которые суть компоненты вектора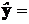 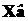. График этого полинома представлен на рис. 31 пунктирной линией. В точке 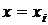показана разность 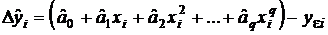между значением в этой точке построенного полинома и результатом измерений. Все эти разности в совокупности для i = 1, 2, . . , kсоставляют вектор

.

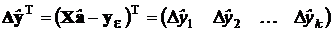Итак, в результате выполненных операций мы определили, что квадратичная форма 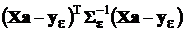принимает минимальное значение при 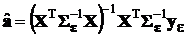. Обозначим это минимальное значение 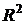. При ОМНК

.

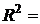
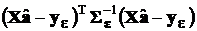Применительно к МНК, когда ,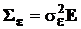

.

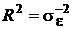
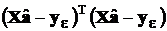В обоих вариантах величина 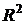случайна, поскольку зависит от выборочных данных. Естественно выяснить плотность распределения величины 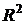. Этот вопрос мы рассмотрим отдельно в следующем разделе.

2.3.7.3. Плотность распределения величины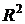

Начнем с рассмотрения величины

,

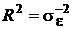
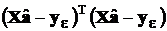которая вычисляется в рамках применения МНК, когда для получения оценок коэффициентов a достаточно знать лишь о факте равноточности измерений, а значение дисперсии 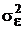погрешностей измерений может быть неизвестным.

В выражении для 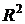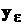– вектор выборочных значений, .

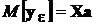Вектор 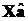– несмещенная ММП-оценка своего математического ожидания 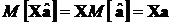. Поэтому 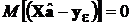. В соответствии с МНК и постановкой задачи в разд.. 2.3.7.1 компоненты 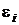вектора случайных погрешностей ε распределены нормально с одинаковыми параметрами 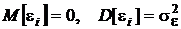. Поэтому компоненты вектора 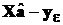, то есть разности

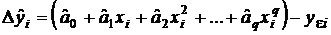
При равноточных измерений можно считать выборочными значениями погрешностей, изъятыми из одной нормальной генеральной совокупности 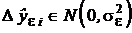. Тогда реализуется МНК, и значение 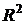представляет собой сумму

,

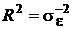
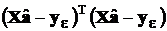
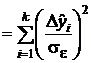где дробь 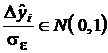, а сумма квадратов этих дробей есть не что иное, как сумма квадратов нормальных случайных величин с нулевым математическим ожиданием и единичной дисперсией.

Такая сумма распределена по закону 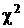с числом степеней свободы, равным количеству слагаемых k , уменьшенному на количество связей между выборочными значениями. В данном случае количество таких связей равно количеству уравнений, из которых получены оценки коэффициентов а, то есть q + 1. Поэтому число степеней свободы k – q – 1.На этом основании заключаем, что

,

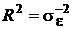
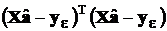
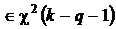Ранее, в одномерном случае в разд. 2.3.4.2. в) было обнаружено, что распределению 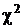с n – 1 степенью свободы подчиняется величина 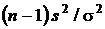. Это также сумма

.

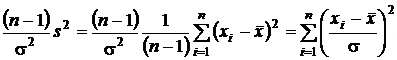Поэтому по аналогии с величиной 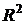мы можем заключить, что при однократных равноточных измерениях несмещенной оценкой дисперсии погрешностей этих измерений может служить величина

=

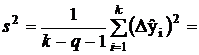
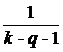
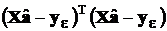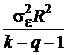
При k = q + 1 это выражение теряет смысл. Подобная ситуация возникает в одномерном случае, когда математическое ожидание исследуемой случайной величины неизвестно и выполняется только одно измерение, то есть n = 1. Тогда оценить характеристику разброса, каковой является дисперсия, принципиально невозможно (см. также разд. 2.3.4.2. b). Поэтому при организации эксперимента необходимо обеспечивать k > q + 1.

При применения ОМНК также

.

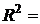
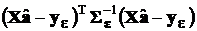
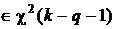По материалам настоящего раздела см. также [5, 7].

2.3.7.4. Практически важные замечания

З а м е ч а н и е 1. При однократных измерениях применение ОМНК затруднено тем, что ковариационная матрица в большинстве случаев неизвестна. Реально известными могут быть только дисперсии 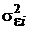случайных погрешностей 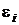из нормативной документации на средство измерений, применяемое для измерения значений функции y = f(x). В этой ситуации ковариационная матрица вынужденно оказывается неполной: в ней остаются только диагональные элементы 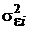, а внедиагональные элементы, которые характеризуют степень корреляции между результатами измерений, отсутствуют. Возникает естественный вопрос о том, как влияет недостаток этой информации на качество получаемых оценок.

Исследования показывают, что неучет корреляции в пределах 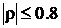приводит лишь к незначительной потере эффективности оценок. Оценки остаются несмещенными.

В случаях, когда при неравноточных измерениях применяется МНК, то есть когда неравноточность не учитывается, в оценках коэффициентов появляется нежелательное смещение.

З а м е ч а н и е 2. Отличие фактической плотности распределения погрешностей 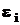от нормальной приводит к потере эффективности оценок среди всех возможных. Однако на множестве всех линейных оценок, то есть оценок, которые линейно зависят от экспериментальных данных, ОМНК и МНК- оценки эффективны для любых плотностей распределения погрешностей 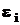. Это означает, что при каждом конкретном виде плотности распределения может быть получена более эффективная оценка, чем оценка ОМНК или МНК, но она обязательно будет нелинейно зависеть от экспериментальных данных.

З а м е ч а н и е 3. Нестатистический вариант полиномиальной аппроксимации сложных функций.

Этот вариант может возникать при желании упростить представление и(или) вычисление сложных функций. В этом варианте в качестве исходных данных совместно используются:

значения аппроксимируемой функции, вычисленные на компьютере с высокой точностью, или табличные значения, взятые из математических или иных справочников;

заданная исследователем точность аппроксимации в виде неравенств типа .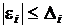

Если заданные значения 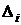одинаковы, то можно применить МНК с подбором подходящей степени полинома q по признаку удовлетворения требований к точности аппроксимации.

При различии значений 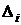можно применить ОМНК, а в качестве ковариационной матрицы 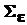использовать диагональную матрицу с элементами в диагонали, равным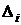и или 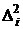– по усмотрению исследователя. Степень полинома, необходимая для достижения требуемой точности аппроксимации, подбирается путем проб.

В этой ситуации статистические и вероятностные термины и характеристики не применяются.

З а м е ч а н и е 4. Все установленные выше свойства ОМНК и МНК- оценок коэффициентов аппроксимирующих полиномов справедливы только тогда, когда модель, то есть вид полинома (степенной полином) и его степень известны. Если фактическая степень полинома выше, чем q, то получаемые оценки коэффициентов будут смещены, и оценки не будут обладать теми свойствами, которые были обнаружены выше в разд. 2.3.7.2, 2.3.7.3. Оценки коэффициентов будут смещены, а плотность распределения величины 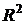не будет соответствовать распределению “хи-квадрат”.

2.3.7.5. Измерения многократные,

характеристики погрешностей известны

Полагаем, что известны характеристики погрешностей измерения 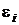значений 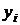аппроксимируемой функции:

при равноточных измерениях – дисперсия ,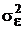

при неравноточных измерениях – ковариационная матрица .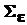

В частном случае ковариационная матрица может быть диагональной, i-ми элементами диагонали являются дисперсии 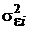погрешностей измерения значений 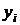аппроксимируемой функции.

При каждом значении аргумента 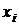, i = 1, 2, ..., k, выполняется n измерений функции. Обозначим результаты этих измерений 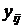, где j–номер эксперимента, j = 1, 2, ..., n.Вычисляются средние арифметические значения

,

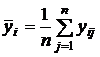из которых составляется вектор 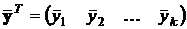, после чего в зависимости от обстоятельств вычисляются МНК или ОМНК-оценки коэффициентов аппроксимирующего полинома по формулам разд. 2.3.7.2, где вместо вектора 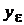следует использовать вектор .

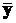В силу центральной предельной теоремы плотность распределения среднего арифметического стремится к нормальной довольно быстро при любых плотностях распределения исходных погрешностей, которые не слишком сильно различаются по дисперсии (см. разд. 1.6.6.4). Поэтому при многократных измерениях требование к нормальности распределения погрешностей измерений значительно смягчается.

Как известно из разд. 2.3.4.1, дисперсии средних арифметических 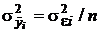. Точно так же из разд. 2.3.4.4 следует, что ковариационная матрица вектора средних арифметических 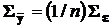. В связи с этими обстоятельствами формулы разд. 2.3.7.2, 2.3.7.3 несколько изменятся.

а)П р и м е н е н и е МНК.

, ,

,

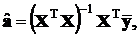
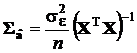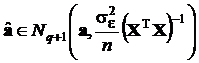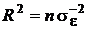
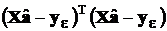но, как и прежде, .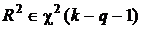

б) П р и м е н е н и е ОМНК.

, , ,

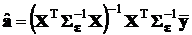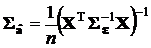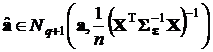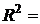n ,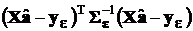

но, как и прежде, .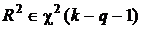

2.3.7.6. Измерения многократные,

характеристики погрешностей неизвестны

В разделе 2.3.7.5 предполагалось, что ковариационная матрица 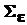или, по крайней мере, дисперсии 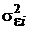погрешностей результатов измерений известны, что на практике бывает достаточно редко, особенно в отношении ковариационной матрицы.

Однако при многократных измерениях предоставляется возможность оценить дисперсии 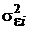при каждом i:

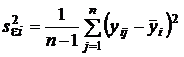
или ковариационную матрицу в целом.

Корректная оценка всех элементов ковариационной матрицы 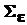, не только диагональных, но и внедиагональных возможна лишь при выполнении специально организованного эксперимента.

Выполняется один цикл измерений в такой последовательности:

воспроизводится значение физической или иной величины, соответствующее первому значению аргумента 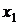и выполняется измерение (определение) значения функции, полученный результат – ;

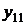воспроизводится значение физической или иной величины, соответствующее второму значению аргумента 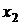и выполняется измерение (определение) значения функции, полученный результат – ;

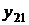описанная процедура продолжается до достижения последнего, k-го значения аргумента х, таким образом будет получен первый вектор результатов измерений ;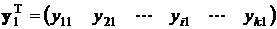

устанавливается значение физической величины x, превышающее значение 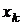, затем вновь устанавливается значение 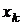, и процесс повторяется, но в обратном порядке, при уменьшении значений x; таким образом будет получен второй вектор результатов .

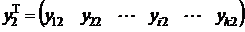При повторении подобных циклов измерений в конечном итоге будет получено четное количество n векторов вида

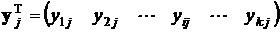, j = 1, 2, . . . , n.

По этому массиву экспериментальных данных вычисляются оценки (см. разд. 2.3.4.3, 2.3.4.4) :

, .

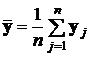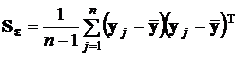Оценка ковариационной матрицы построена в соответствии с ее математическим определением, приведенным в разд. 1.7.3. Поскольку при реализации ОМНК эту матрицу придется обращать, она не должна быть особенной. Для этого необходимо, чтобы n > k. Но если по техническим, экономическим или иным причинам это условие выполнить невозможно, то придется ограничиться вычислением только оценок дисперсий 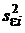при каждом значении 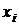. По этим значениям строится диагональная матрица 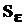, в диагонали которой на i-м месте стоит оценка дисперсии 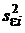. В таком случае не учитывается ковариация между измерениями в точках 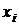, что приводит к незначительной потере в эффективности оценок коэффициентов, но они остаются несмещенными (см. разд.2.3.7.4, замечание 1).

После этого для вычисления оценок коэффициентов аппроксимирующего полинома применяется ОМНК с заменой во всех формулах разд. 2.3.7.5 матрицы 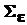на :

, , ,

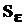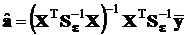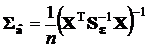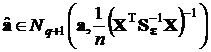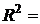n ,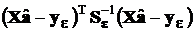

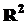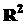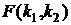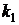Вследствие случайности исходных данных величина также случайна. Из-за того, что в формуле для вместо генеральной ковариационной матрицы участвует ее оценка, распределение “хи-квадрат” неприменимо. Вместо него здесь применяется плотность F-распределения Фишера (иногда она именуется, как плотность распределения Фишера-Снедекора), и обозначается, как , где и 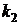– количества степеней свободы. Плотность распределения Фишера имеет случайная величина [5]

F= ,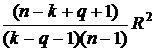

что записывается в виде

F = .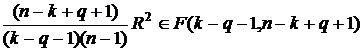

Эта плотность распределения широко используется для сопоставления дисперсий генеральных совокупностей при дисперсионном анализе посредством исследования отношения оценок этих дисперсий. Нетрудно увидеть, что величина 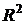также, в некотором смысле есть отношение дисперсий. Функция распределения Фишера табулирована, таблицы приводятся в специальных таблицах математической статистики (например, [1,13, 14]).

Из последних выражений для величины F следует, что при подготовке эксперимента по аппроксимации зависимостей необходимо обеспечить неравенство n > k - q -1. Это неравенство выполняется всегда, поскольку для предотвращения особенности матрицы 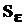необходимо выполнить неравенство n > k, которое означает превышение количества повторных измерений над количеством точек, в которых выполняется эксперимент. Иногда по техническим, экономическим или иным объективным причинам это условие оказывается невыполнимым. В таком вынужденном случае придется формировать диагональную матрицу :

, ,

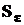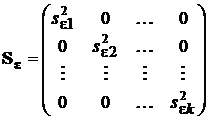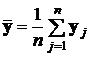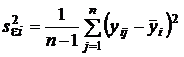
и применять ее при вычислении оценок коэффициентов.

В этой ситуации должно быть k > q + 1, и F‑распределению Фишера подчиняется случайная величина

F= .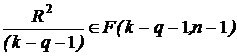

Число степеней свободы k - q - 1 и n - 1.

В частном случае, когда по результатам проверки по критерию Кочрена (п. 2.5.6.1) гипотезы о равенстве дисперсий 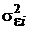будет принято решение о применении МНК, вычисляется средняя оценка дисперсии

,

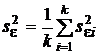которая подставляется вместо 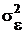во всех соответствующих формулах разд. 2.3.7.5

, ,

,

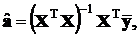
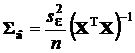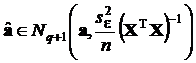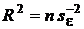
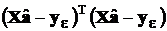И в этом случае случайная величина

F= .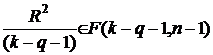

распределена в соответствии с F-распределением Фишера с числом степеней свободы k - q - 1 и n - 1.

Все замечания, сделанные выше в разд. 2.3.7.4, распространяются на случаи многократных измерений в полном объеме.

2.3.7.7. Особенности вычислений при реализации МНК и ОМНК

Как следует из разд. 2.3.7.2, 2.3.7.3, в процессе оценивания коэффициентов аппроксимирующих полиномов приходится обращать матрицы 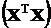и 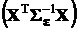. Из линейной алгебры и вычислительной математики известно, что устойчивость результатов подобных действий в сильной степени зависит от обусловленности обращаемых матриц. Что касается матриц 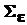и 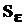, то здесь следует опасаться того, что они могут оказаться особенными. В частности, одна из причин появления особенности у матрицы 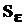указана в разд. 2.3.7.6.

Обусловленность матриц характеризуется числом обусловленности, которое есть не что иное, как коэффициент “усиления” погрешностей экспериментальных данных и погрешностей округления к погрешностям результатов вычислений.

Для квадратных симметричных матриц, каковыми являются матрицы, перечисленные выше, число обусловленности определено равенствами

,

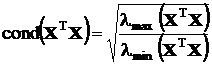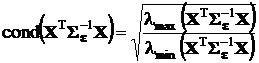
где 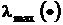, 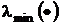– наибольшее и наименьшее собственные числа соответствующей матрицы.

Число обусловленности матриц, используемых в МНК или в ОМНК, может достигать значений от 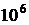до 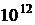и выше.

Известно, что число обусловленности указанных матриц монотонно возрастает с увеличением количества столбцов матрицы X, то есть с увеличением порядка q или, что то же самое, с увеличением числа коэффициентов полинома (см. конструкцию матрицы X в разд. 2.3.7.2). Максимального значения число обусловленности достигает при q + 1 = k, когда распределение Фишера уже неприменимо. Особенно опасной оказывается ситуация, когда количество оцениваемых коэффициентов превышает их фактическое количество, то есть при завышении степени полинома.

Можно рекомендовать три способа повышения устойчивости оценок коэффициентов МНК и ОМНК.

1. Не стремиться к излишне высокому порядку аппроксимирующего полинома, использовать априорную информацию о гладкости аппроксимируемой функции.

2. При необходимости аппроксимации функции y = f(x) полиномом высокого порядка вплоть до q = k – 1 использовать метод регуляризации Тихонова.

Применительно к МНК и ОМНК этот метод заключается в следующем [7].

Исходное уравнение преднамеренно искажается таким образом, чтобы это искажение заведомо улучшало обусловленность. Таким регуляризирующим искажением является, по Тихонову, увеличение диагональных элементов матрицы системы уравнений. Регуляризированное таким образом решение имеет вид .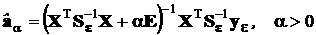

Число a называется параметром регуляризации. Оценка 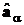в англоязычной литературе называется ридж-оценкой. В отечественной литературе встречается калькоподобный перевод этого термина: “гребневая оценка”.

Эта оценка, конечно, смещена. Ее смещение примерно

.

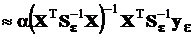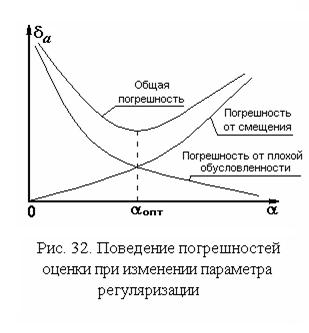Проблема состоит в выборе такого значения параметра регуляризации, при котором результирующая погрешность, вызванная смещением оценки и плохой обусловленностью матрицы системы, была минимальной.

На рис. 32 показана принципиальная возможность такого выбора. Однако, универсального практического рецепта выбора оптимального значения параметра регуляризации пока не существует.

3. Третий способ заключается в таком размещении значений аргумента x, при котором число обусловленности матрицы 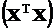или 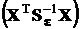было минимальным. Этот способ рассматривается в следующем пункте.

2.3.7.8. Основные принципы планирования эксперимента,