Двумерная нормальная плотность распределения

Вновь обозначим: 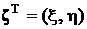– нормальный случайный вектор, 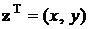– значения, которые он принимает. Двумерная нормальная плотность распределения записывается в виде

,

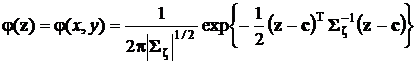где 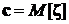– двумерный вектор – математическое ожидание случайного вектора ζ, 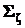– ковариационная матрица вектора ζ, 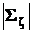– ее определитель

, , .

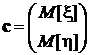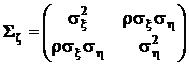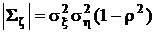Индексы у обозначения коэффициента корреляции r опущены, поскольку здесь это не вызовет никаких осложнений.

В дальнейшем принадлежность случайного вектора двумерному нормальному распределению будем записывать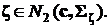

Форма и свойства двумерной нормальной плотности распределения определяются, в основном, показателем степени экспоненты и не зависят от ее расположения, а потому примем 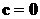. В связи с этим рассмотрим показатель степени экспоненты отдельно:

.

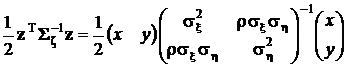Обращение матрицы выполним через алгебраические дополнения и определитель:

.

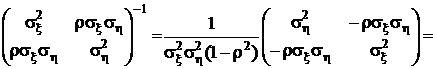
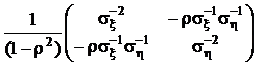Тогда

.

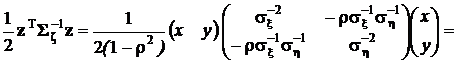
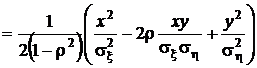Если нормальные случайные величины xиh некоррелированы, то есть r = 0, то показатель степени экспоненты упрощается очевидным образом, и двумерная нормальная плотность распределения распадается на два сомножителя:

,

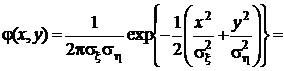
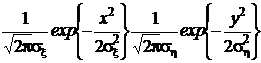каждый из которых есть не что иное, как маргинальная плотность распределения каждой из компонент вектора ζ. Из этого факта мы получаем полезный вывод:

Из некоррелированности двух нормально распределенных случайных величин с необходимостью следует их независимость; это исключительное свойство нормальных случайных величин, которое является их характеризационным признаком, а именно, если для двух случайных величин установлено, что из некоррелированности следует их независимость, то эти случайные величины распределены нормально.

Проанализируем геометрическую форму поверхности, которая задана нормальной плотностью распределения.

Очевидно, что эта поверхность имеет максимум в точке 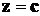, поскольку при любом отклонении от этой точки абсолютная величина показателя степени экспоненты возрастает, а из-за того, что этот показатель степени меньше нуля, функция в целом убывает. Значение максимума в указанной точке равно множителю перед экспонентой.

Для исследования формы поверхности примем 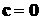и рассечем ее плоскостью, параллельной плоскости x0y на уровне B, ниже максимального значения. Указанное рассечение выражается равенством

.

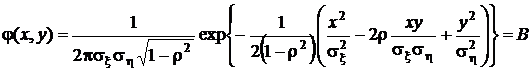В сечении получим фигуру, описываемую уравнением

.

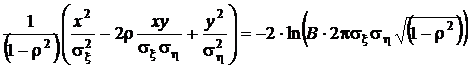Обозначим 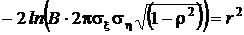, тогда уравнение фигуры, получившейся в сечении, принимает знакомый вид:

.

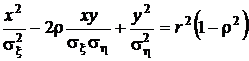Это уравнение эллипса, размеры и расположение которого определяются его параметрами: радиусом 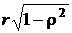, который увеличивается с уменьшением B, то есть с приближением секущей плоскости к плоскости x0y, длинами полуосе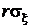й и 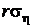, а также коэффициентом корреляции r. Пример одного из сечений приведен на рис. 25. Непосредственно из уравнения эллипса видно, что точки его пересечения с осями координат суть 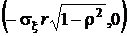, 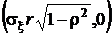– с осью x, и 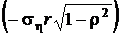, 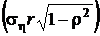– с осью y. Угол наклона большой оси к оси абсцисс

.

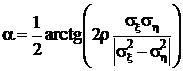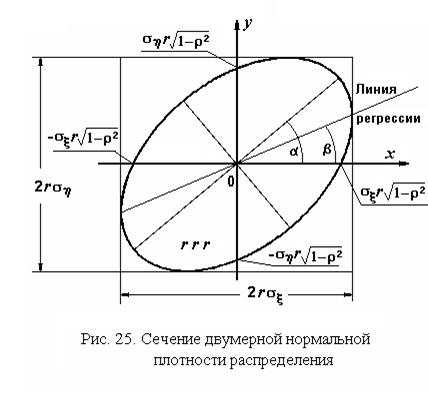При изменении коэффициента корреляции в диапазоне от -1 до 1 все эллипсы остаются вписанными в прямоугольник со сторонами 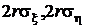. При r = 0оси эллипса совпадают с осями координат, при r = -1и при r = +1точки его пересечения с осями перемещаются в начало координат, и эллипс вырождается в прямую линию. Это говорит о том, что в таких крайних случаях из-за жесткой связи между случайными величинами для их размещения хватает одной прямой, то есть по-существу, мы имеем дело не с двумя, а с одной случайной величиной, как это уже указывалось в разд. 1.7.3.

На рис. 25 показана еще одна прямая, поименованная как линия регрессии. Эта линия есть геометрическое место точек, которые представляют все условные математические ожидания M[h/x = x].

Для того чтобы получить уравнение этой линии, найдем выражение для условной плотности распределения, для чего воспользуемся соответствующей формулой из разд. 1.7.1, помня о том, что маргинальные плотности двумерного нормального распределения также нормальны:

.

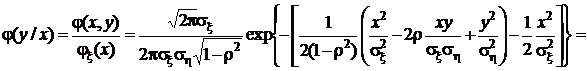
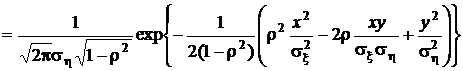В фигурных скобках имеет место полный квадрат разности, поэтому

.

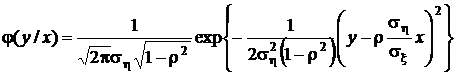Полученное выражение есть каноническая запись одномерной нормальной плотности распределения с параметрами:

дисперсия равна ;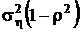

математическое ожидание равно .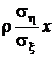

Таким образом, мы получили условную плотность распределения, которая оказывается также нормальной, и условное математическое ожидание 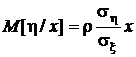, которое является линейной функцией x . Напомним, что в начале настоящего пункта мы приняли равными нулю математические ожидания обеих компонентов случайного вектора 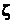. Настало время вспомнить об этом и записать условное математическое ожидание для общего случая:

.

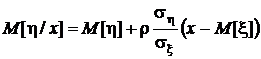Полученное выражение называется уравнением линейной регрессии случайной величины h на случайную величину x. Угол наклона линии регрессии к оси абсцисс

.

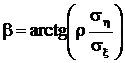Регрессия между двумя нормальными случайными величинами (если она существует, то есть когда r ¹ 0) всегда линейна. Это естественно, поскольку только линейное преобразование не изменяет вид плотности распределения.

Прямая регрессии обязательно проходит через середины вертикальных хорд эллипса, потому что условные нормальные распределения, которые являются сечениями двумерной плотности вертикальными плоскостями, симметричны, и их математические ожидания совпадают с модами и медианами этих сечений. И поэтому прямая регрессии пересекается с эллипсом в точках касания вертикальных касательных к нему.

Заметим также, что частные (маргинальные) плотности двумерной нормальной величины также нормальны.