Функции распределения и плотности распределения

Рассмотрим двумерный случайный вектор, то есть двумерный вектор, каждая составляющая которого есть непрерывная случайная величина:

.

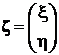Как и ранее, случайный вектор и его случайные компоненты обозначим греческими буквами, а значения, которые может принимать вектор и его компоненты – соответствующими латинскими буквами, то есть будем считать, что случайный вектор ζ принимает значения

.

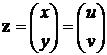Функция распределения двумерного случайного вектора есть вероятность совместного осуществления событий:

.

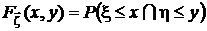Плотность распределения, как и ранее, есть производная от функции распределения по обоим аргументам:

,

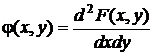поэтому

.

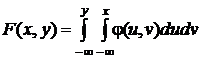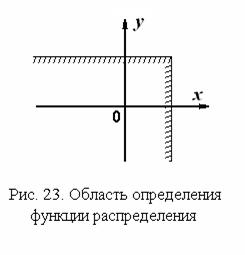
Область интегрирования показана на рис. 23.

В силу монотонности вероятностной меры функция распределения – неубывающая функция по каждому аргументу, поэтому плотность распределения есть неотрицательная функция двух аргументов, которая описывает некоторую поверхность над координатной плоскостью. Эта поверхность приближается к плоскости x0y при удалении значений аргументов от начала координат в любом направлении. Понятно, что

.

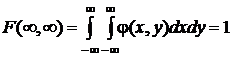Если по одному из аргументов ограничений нет, то

.

.

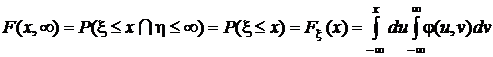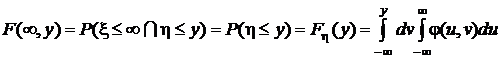Таким образом мы получили маргинальные (частные) функции распределения 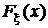и 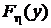. Дифференцирование этих функций по их аргументам, то есть дифференцирование соответствующих интегралов по их верхним пределам, по определению, дает маргинальные (частные) плотности распределения:

, .

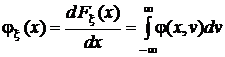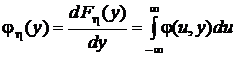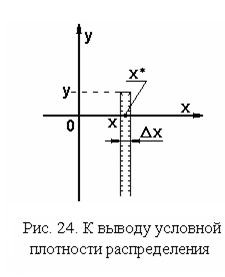Определим условную функцию распределения, то есть функцию распределения одной из случайных величин при условии, что другая случайная величина принимает некоторое конкретное значение, например,

.

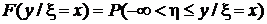Выделим на координатной плоскости область, показанную на рис. 24.

Вероятность того, что случайный вектор принимает значения из этой области, равна 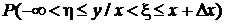. В соответствии с формулой для условной вероятности из разд. 1.2.3

.

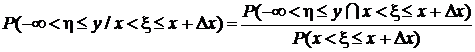Условная функция распределения получается в результате предельного перехода:

.

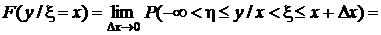
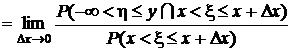
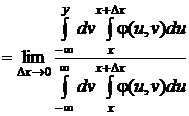По теореме о среднем, внутри интервала 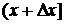найдется точка 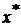, такая, что

,

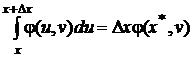поэтому

.

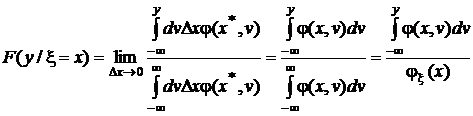Условная плотность распределения есть производная от условной функции распределения:

.

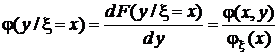Аналогично

.

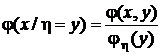Обычно обозначают 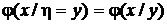и 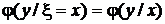. В этих обозначениях из полученных формул следует

, .

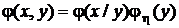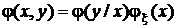С учетом этих соотношений перепишем формулы для маргинальных распределений в виде:

, .

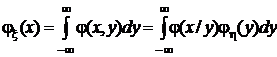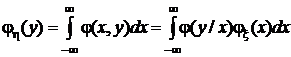Это формулы полной вероятности для непрерывных случайных величин.

Поскольку 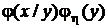= 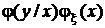, получаем формулу Байеса для непрерывных случайных величин:

.

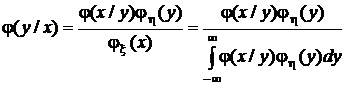Если x и h независимы, то 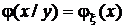, 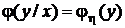и поэтому .

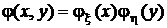Справедливо и обратное: если 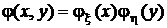, то из этого с необходимостью следует независимость x и h.

Признак независимости случайных величин: две случайные величины независимы тогда и только тогда, когда их совместная плотность распределения может быть представлена как произведение маргинальных плотностей распределения этих величин (см. также разд. 1.2.3).

Числовые характеристики

Моменты случайных величин определяются, как и ранее, следующими формулами

начальные моменты k-го порядка

,

;

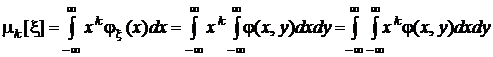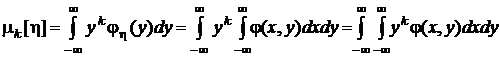центральные моменты k-го порядка:

, .

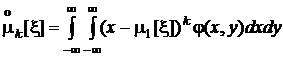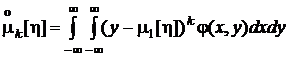Среди этих моментов самыми употребительными являются математи­ческие ожидания

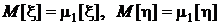
и дисперсии

, .

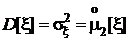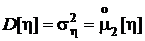Математическое ожидание случайного вектора есть вектор, компонентами которого являются математические ожидания соответствующих составляющих:

.

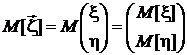Из условных моментов выделим лишь первые начальные (условные математические ожидания) и вторые центральные (условные дисперсии):

, ,

,

.

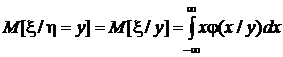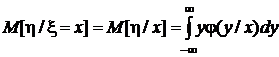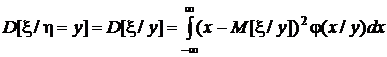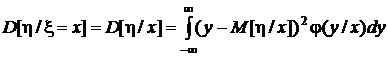Как и ранее, во всех случаях

, ,

, .

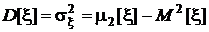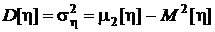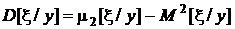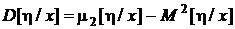Для двумерных случайных величин вводятся смешанные моменты:

начальные порядка k, r

;

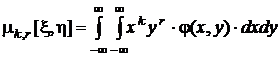центральные порядка k, r

.

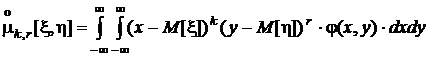Из них наиболее употребительным является центральный смешанный момент порядка (1, 1),который называется ковариацией и обозначается cov(x, h):

.

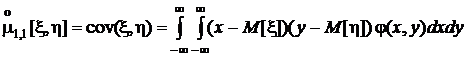Выясним связь между этим и начальным смешанным моментом того же порядка:

.

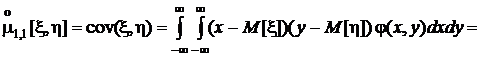
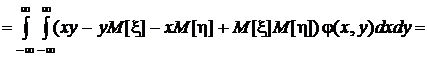
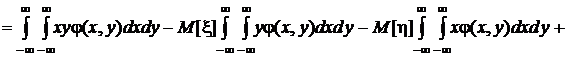
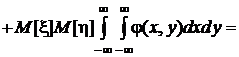
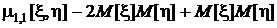В итоге получаем, что .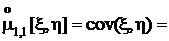

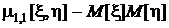Если случайные величины x и hнезависимы,в соответствии с признаком независимости, сформулированным ранее,

= ,

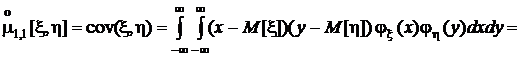
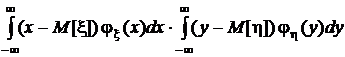то есть мы видим, что двукратный интеграл в этих условиях преобразуется в произведение однократных интегралов, каждый из которых равен 0. В самом деле,

.

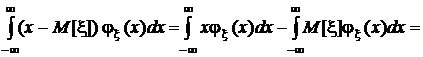
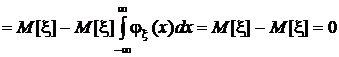Поэтому при условии независимости случайных величин x и hих первый центральный смешаный момент, или ковариация, равна 0.

При взаимно однозначной зависимости между x и h, например, линейной 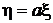, ковариация

.

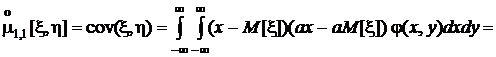
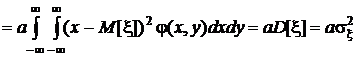Это означает, что ковариация есть характеристика степени зависи­мости между случайными величинами. Для того, чтобы избавиться от масштаба значений, принимаемых случайными величинами, в качестве показателя линейной зависимости используется частное от деления ковариации на произведение среднеквадратических значений случайных величин:

.

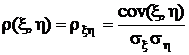Эта величина называется коэффициентом корреляции. Случайные величины, у которых коэффициент корреляции равен нулю, называются некоррелированными. Независимые случайные величины с необходимостью некоррелированы. Обратное, вообще говоря, неверно! Из некоррелированности случайных величин их независимость, вообще говоря, не следует. Это понятно хотя бы потому, что из равенства нулю центрального смешанного момента порядка (1, 1) вовсе не следует, что все центральные смешанные моменты более высоких порядков также равны нулю.

Определим максимально возможное значение коэффициента корре­ляции. Естественно предположить, что своего максимального значения коэффициент корреляции достигает при взаимно однозначной связи между x и h,например, линейной 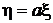. Для этого случая нам известна ковариация междуx и h, а из разд. 1.6.5 следует, что 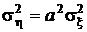, то есть 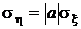. В результате получаем

,

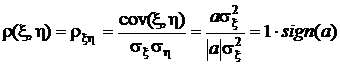а это означает, что