Функции от непрерывных случайных величин

Вначале введем и кратко опишем гамма-функцию, которая встретилась в разд. 1.6.6.7 и будет встречаться в дальнейшем.

Введем математическое определение гамма-функции и применим интегрирование по частям:

,

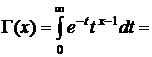
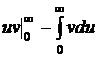где , , , .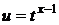

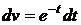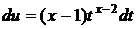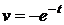Выполним подстановку:

= .

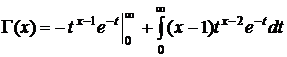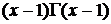В результате мы получили рекуррентную формулу для вычисления значений гамма-функции.

Если x – целое положительное число, x = n, то в соответствии с этой рекуррентной формулой

.

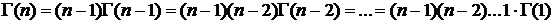Вычислим G(1) отдельно:

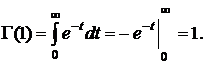
Поэтому 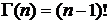В частности, G(1) = 0×Г(0) = 0! = 1.

В дальнейшем нам понадобятся следующие значения гамма-функции от дробных аргументов:

, , .

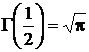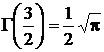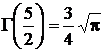Последние два значения гамма-функции получены с использованием только что выведенной рекуррентной формулы.

Займемся теперь основной задачей. Пусть задана непрерывная дифференцируемая функция от случайной величины x: h = f (x). Известна плотность распределения случайной величины x: j (x).Задача состоит в том, чтобы найти плотность распределения y(y) случайной величиныh.

Подобная задача возникает в технике, когда случайные процессы или измеряемые величины, возмущенные случайными помехами, претерпевают нелинейные преобразования, и возникает задача прогнозирования характеристик сигнала, который получается в результате этого преобразования.

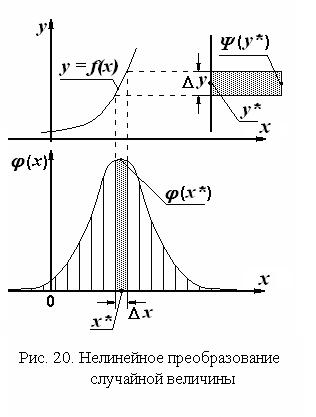Для вывода необходимого соотношения воспользуемся рис. 20, на котором представлены функция преобразования y = f(x) и плотность распределения j(x). Функция преобразования предполагается монотонной, и это свойство функции преобразования практически всегда имеет место в технических устройствах: средствах измерения, измерительных преобразователях и регуляторах. В силу взаимной однозначности преобразования случайная величина h принимает значения из интервала Dy, в точности с той же вероятностью, с которой случайная величина x принимает значения из интервала Dx. Поскольку вероятностная мера интервала есть площадь под кривой плотности распределения на этом интервале, это означает, что площади заштрихованных фигур на рис. 20 должны быть равны

,

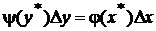где 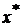, 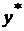– точки, находящиеся внутри выделенных интервалов Dx и 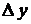, 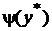– значение искомой плотности распределения в точке .

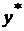Из этого выражения следует:

.

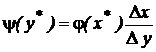Заметим здесь, что ширина интервала 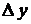, в который преобразуется интервал Dx,не зависит от знака производной функции преобразования, и это обстоятельство мы учтем при выполнении предельного перехода

.

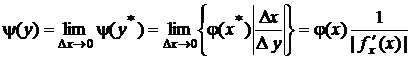В силу инвариантности первого дифференциала производная 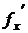выражается через производную от обратной функции:

.

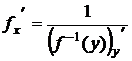Кроме того в выражении для y(y) необходимо выразить аргумент x плотности распределения j(x) через y с помощью обратной функции : 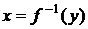. В итоге окончательно получим:

.

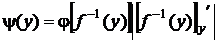П р и м е р ы.

1. Случайная величина x распределена нормально: 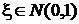. Функция преобразования 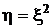. Эта ситуация представлена на рис. 21. Видно, что в силу двузначности обратной функции случайная величина h принимает значения из интервала 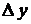, когда случайная величина xпринимает значения в одном из двух выделенных интервалов Dx. Поэтому для данного примера исходное выражение должно быть изменено следующим образом:

.

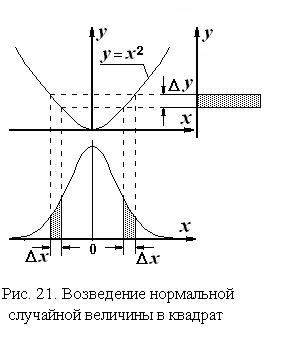
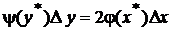Из этого следует соответствующее изменение общей формулы:

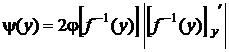
Для данного примера

, ,

,

.

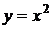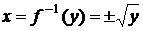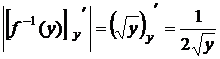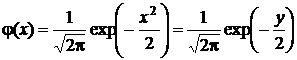В конечном итоге после подстановки в общую формулу получим искомую плотность распределения

.

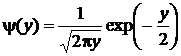Найдем характеристическую функцию этого распределения:

.

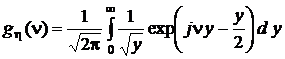Сделаем замену переменной интегрирования:

.

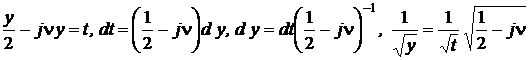В результате этой замены получим выражение с участием гамма-функции:

.

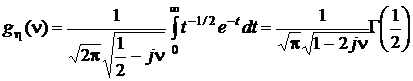Поскольку 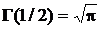, окончательно получим:

.

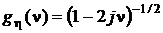2. Пусть 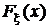– интегральная функция распределения случайной величины x. Образуем случайную величину h, как функцию от случайной величины x : 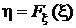.Задача состоит в том, чтобы найти плотность распределенияy (y)случайной величиныh.

Воспользуемся полученным ранее выражением

.

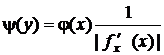В нашем случае в качестве функции y = f(x) выступает функция 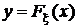, производная от которой по x есть плотность распределения j(x). Поэтому

.

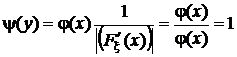Таким образом, оказывается, что случайная величина h, полученная в результате функционального преобразования любой непрерывной случайной величины x путем ее подстановки в ее же интегральную функцию распределения, распределена равномерно в интервале [0,1] вне зависимости от вида функции распределения величины x.

Полученный результат имеет два полезных применения.

Первое. Машинное моделирование случайных чисел с заданной интегральной функцией распределения. Технология моделирования следующая:

задается функция распределенияF(x);

по стандартным программам генерируются случайные числа 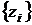, распределенные равномерно в интервале [0, 1];

случайные числа 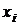, распределенные в соответствии с заданной функцией распределения F(x), получаются как решения уравнений

.

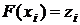Второе. Статистическое оценивание параметров и характеристик случайных величин по результатам экспериментов, вне зависимости от вида распределения исследуемой случайной величины. Это применение будет изложено в разделе 2. Математическая статистика.

3. Случайная величина h образуется в результате линейного преобразования случайной величины : .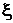

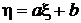В данном случае реализуется функциональное преобразование

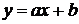, обратная функция 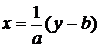, производная от нее по y равна 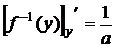. В результате подстановки в общую формулу получим:

.

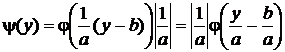Это означает, что любое линейное преобразование не изменяет вид плотности распределения случайной величины. Изменяется лишь масштаб и смещение от начала координат.

Неравенство Чебышева

Неравенство Чебышева позволяет сделать грубую, но быструю оценку вероятности отклонения значений случайной величины от ее математического ожидания, превышающих некоторое заданное положительное значение A: .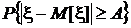

Несмотря на грубость получаемой оценки неравенство Чебышева имеет достаточно широкое и полезное применение благодаря тому, что оно справедливо для любых законов распределения, кроме закона распределения Коши. С одним из таких применений мы познакомимся в разделе 2 «Математическая статистика».

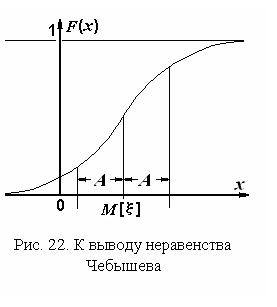
Запишем вероятность, подлежащую оценке, как интеграл от плотности распределения случайной величины x по отрезкам оси

(-¥, M[x]-A], (M[x]+A, ¥),

то есть по множеству 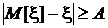, как это видно из рис. 22:

.

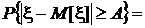
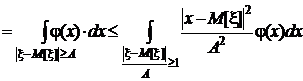
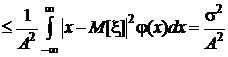Окончательно .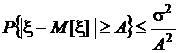

Существуют другие записи неравенства Чебышева:

если A = ks, то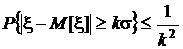

или .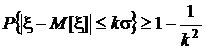

Для того, чтобы оценить степень грубости оценки, вытекающей из неравенства Чебышева, сопоставим ее с точными значениями вероятностей, установленными в разд. 1.6.6.4 для нормально распределенной случайной величины.

Точные значения:

,

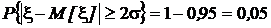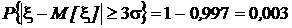
Значения вероятностей, полученных из неравенства Чебышева для тех же отклонений значений случайной величины от математического ожидания:

, .
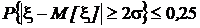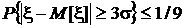