Функция непрерывной случайной величины

Так же, как и в дискретном случае можно ввести функцию непрерывной случайной величины. Пусть имеется случайная величина X, f(x), F(x) и монотонная функция y=j(x), для которой существует обратная дифференцируемая функция x=y(y). Опеределим случайную величину Y=j(x) как числовую функцию, которая каждому элементарному исходу испытания, характеризуемому значением x, ставит в соответствие число, равное j(x). Чтобы определить случайную величину Y, необходимо кроме ее значений задать закон распределения, то есть найти ее функцию распределения G(y) и плотность вероятности g(y). Можно показать, что для этих функций должны выполняться следующие равенства

G(y)= F(y(y)) и g(y)= f(y(y))×y¢(y)

Основные характеристики непрерывной случайной величины

Математическое ожидание

Математическим ожиданием непрерывной случайной величины называется интеграл плотности вероятности

_¥

M(x)= ∫ xf(x)×dx

^-¥

В случае, если функция плотности вероятности отлична от нуля только на интервале a<x<b

_b

M(x)= ∫ xf(x)×dx

^a

Дисперсия

Дисперсией непрерывной случайной величины называют математическое ожидание отклонения случайной величины от ее математического ожидания

_¥

D(x)= ∫[x-M(X)]²×f(x)×dx

^-¥

В случае, если функция плотности вероятности отлична от нуля только на интервале a<x<b

_b

D(x)= ∫[x-M(X)]²× f(x)×dx

^a

Для дисперсии и математического ожидания непрерывной случайной величины выполняются те же свойства, что и для дискретной.

Мода и медиана

Модой непрерывной случайной величины X называют такое значение x_Mo=x₀, для которого функция плотности распределения f(x₀)× максимальна.

Медианой непрерывной случайной величины X называют такое значение x_Me=x₀, для которого функция распределения равна 0.5

P(X< x_Me)= P(X> x_Me)= F(x_Me)=0.5

5.3.4. Моменты k-го порядка

Начальным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание величины величины X^k

_¥

a_k (X)=M(X ^k)= ∫x^k f(x)×dx

^-¥

Центральным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание k-ой степени соответствующей центрированной величины.

_{· ¥}

M_k(X)=M(X ^k)= ∫[x-M(X)]^k×f(x)×dx

^-¥

Асимметрия и эксцесс.

Для характеристики общего вида графика плотности вероятности случайной величины вводят такие параметры, как асимметрия и эксцесс.

Для оценки асимметрии распределения случайной величины можно использовать любой нечетный центральный момент, если его порядок выше первого. Обычно используется нормированный третий момент случайной величины

as=m³/s³=1/s³×M([X-M(X)]³)

При as>0 асимметрия положительна и более длинное крыло кривой распологается справа от математического ожидания. При as<0 асимметрия отрицательна и «длинна часть» кривой распологается слева от математического ожидания. Для симметричного распределения as=0.

Эксцесс теоретического распределения вводится как

Ek=m⁴/s⁴-3.

Если случайная величина распределена в соответствии с нормальным законом, Ek=0. При Ek<0 – функция плотности распределения имеет более низкую и плоскую вершину, чем в случае нормального распределения, при Ek>0 – более высокую и острую вершину.

Законы распределения непрерывной случайной величины

Равномерное распределение

Распределение называется равномерным, если плотность вероятности постоянна на интервале a<x<b и равна 0 вне интервала.

0, x£a

f(x)= 1/(b-a), a<x£b

1, x>b

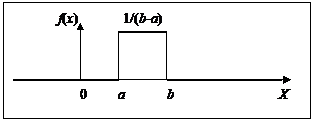Рис. 8. Равномерное распределение (плотность распределения)

Пользуясь свойствами функции распределения легко показать, что

При x£a функция

_x

F(x)= P(-¥<X< x)= ∫ f(t)×dt=0

^-¥

При a<x£b функция

_0x

F(x)=P(-¥<X<x)= ∫ f(t)×dt + ∫ f(t)×dt=x/(b-a)

^{-¥ a}

При x>b F(x)=P(-¥<X< x)=1

_{0 b x b}

F(x)=P(-¥<X<x)= ∫ f(t)×dt + ∫ f(t)×dt +∫ f(t)×dt =∫1/(b-a)dx=(b-a)/(b-a)=1

^{-¥ a b a}

Таким образом,

0, x£a

F(x)= (x-a)/(b-a), a<x£b

1, x>b

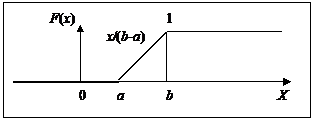Рис. 9. Равномерное распределение (функция распределения)

Математическое ожидание для равномерного распределения

_{b b b}

M(x)= ∫ xf(x)×dx=∫1/(b-a) xdx=1/2×x²/(b-a)½=(b²- a²)/(b-a)/2=(a+b)/2

^{a a a}

Дисперсия равномерного распределения

_b

D(X)=M([X]²)-[M(X)]²=∫x²/(b-a)dx-[(b+a)/2]²=(b-a)²/12

^a

Мода для равномерного распределения не существует, медиана x_Me==(a+b)/2.

Показательное распределение

Показательное распределение задается функцией

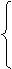le^-lx, x³0

f(x)=

0, x<0

Функция распределения

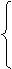1-e^-lx, x³0

F(x)=

0, x<0

Зная функцию распределения легко определить вероятность попадания случайной величины в заданный интервал

P(a<x<b)= F(b)- F(a)= e^-la- e^-lb

Математическое ожидание и дисперсия для показательного распределения равны

M(x)=1/l

D(x)=1/l²

Из условия

F(x_Me)=0.5=1- e^-lxMe

получим для медианы значение

x_Me=ln(0.5)/(-l)

Мода показательного распределения равна 0

Нормальное распределение

Нормальное распределение описывается законом

f(x)= 1/s/(2p)^0.5×e^-1/2×(x-a)2/s²

Данный закон распределения зависит отдвух праметров – a и s. Можно показать, что

M(x)= a

D(x)= s²

График плотности нормального распределения называют нормальной кривой (кривой Гаусса), а соответствующую функцию - функцией Гаусса. Данная функция определена для всех значений x, симметрична относительно x=a, на бесконечности она стремится к 0, максимальна при x=a, f(a)= 1/s/(2p)^0.5. Точки перегиба - x=a+s и - x=a-s.

Нормальное распределение называется нормированным при

M(x)=0

D(x)= 1

Значения нормированной функции нормального распределения

j(x)= 1/(2p)^0.5×e^-x2/2

затабулированы. Вероятность случайной величины оказаться в заданном интервале в случае ее нормированного нормального распределения определяется выражением

x₂

P(x₁<x<x₂)= 1/(2p)^0.5×∫ e^-t2/2×dt=F(x₂)-F (x₁),

x₁

где

x

F(x)= 1/(2p)^0.5×∫ e^-t2/2×dt

0

- уже знакомая нам функция Лапласа. Если случайная величина распределена нормальным образом с параметрами a и s (не нормирована), тогда

P(x₁<x<x₂)=F((x₂- a)/s)-F((x₁- a)/s),

Используя эту формулу, легко найти вероятность того, что отклонение случайной величины от математического ожидания не превысит величину e

P(|x -a|£e)= P(a -e£x £ a +e)=F(( a -e- a)/s)-F(( a +e- a)/s)=2×Ф(e/s)

В случае, если e=3s

P(a -3s£x £ a +3s)=2×Ф(3)= 2×0.49865=0.9973

Таким образом, с вероятностью 99.73% значения нормально распределенной случайной величины находятся в интервале
(a -3s, a +3s). Данное утверждение получило название правила “трех сигм”. Вероятность того,что отклонение математического ожидания превысит 3s составляет всего 0.0027. На практике обычно предполагают, что если закон распределения случайной величины неизвестен, но правило трех сигм выполняется, распределение можно считать нормальным.

Закон больших чисел