Пространство элементарных исходов

Мощность множества измеряется не в лошадиных силах, а в кардинальных числах. Бывают множества с конечной, счетной, континуум мощностью и даже больше. Если элементы множества можно пересчитать,то есть поставить в взаимно однозначное соответствие каждому элементу множества натуральное число, оно называется «счетное множество».

Множество элементарных исходов опыта в теории вероятностей называется пространством элементарных исходов. Элементарные исходы являются элементами (точками) этого множества. В предыдущих примерах видно, что одному реальному опыту можно сопоставить несколько описаний пространства элементарных исходов. Таким образом, для описания экспериментов в качестве первичных математических понятий используются множества. В своей общей части теория вероятностей не использует никаких специфических свойств элементарных исходов и множеств, кроме числа элементов в них или их мощности. Поэтому любые два пространства элементарных исходов с одинаковым числом элементов или одинаковой мощностью с точки зрения теории вероятностей эквивалентны. Например, в опыте с бросанием монеты мы можем выбрать в качестве исходов слова "герб" и "решка" или числа "0" и "1". Обозначается пространство элементарных исходов обычно так: а сам элементарный исход так Можно записать отношение между пространством элементарных исходов и элементарными исходами так

Советы по построению пространства элементарных исходов.

Имейте в виду задачу, которую вы хотите решить - то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.

На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.

Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.

Очень удобно выбирать элементарные исходы в виде векторов (в смысле точек в пространстве), размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.

Определения

Подмножества

Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.

· Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.

· Элементарный исход можно представить в виде

· ,

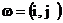· где i – число очков на первой кости, j – второй кости.

· Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:

·

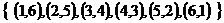
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…

A =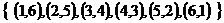

Пустое подмножество обозначим

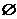
Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.

Множество всех элементарных событий W называется, естественно, достоверное событие.

Элементарный исход как случайное событие представляет собой одноточечное подмножество.

Операции над подмножествами

Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию.

Дополнение

Дополнение до подмножества A - это подмножество

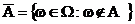
т. е. дополнением к A является подмножество, включающее в себя все элементарные исходы, не содержащиеся в A. С точки зрения теории вероятностей подмножество A представляет событие, которое естественно назвать отрицание A или не-A. Т.е. A в опыте не произошло («не наступило»).

Объединение

Объединением двух подмножеств A и B является подмножество

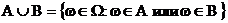
Соответственно и интерпретация : произошло или A или B.

Пересечение

Пересечением двух подмножеств : A и B является подмножество

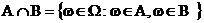
Соответственно и интерпретация : и A и B произошли одновременно.

Разность

Разностью двух подмножеств A и B является подмножество

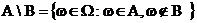
Соответственно и интерпретация : A произошло, B - нет.

Симметричная разность

Симметричной разностью двух подмножеств A и B является подмножество

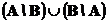
Соответственно и интерпретация : произошло только одно из этих двух событий.