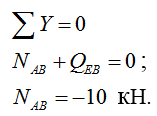Узловая передача нагрузки (многопролетные балки)

Внешняя нагрузка на несущую часть строительной конструкции может передаваться через вспомогательные балки (например, в мостах).

Основная балка, которая является несущей частью, называется главной балкой. Балки, расположенные перпендикулярно к главной, называются поперечными. Однопролетные балки, к которым непосредственно приложена внешняя нагрузка, называются продольными (вспомогательными).

Описанный способ передачи нагрузки на главную балку называется узловым, а точки главной балки, к которым примыкают поперечные балки, называются узлами. Участок балки между двумя соседними узлами называют панелью.

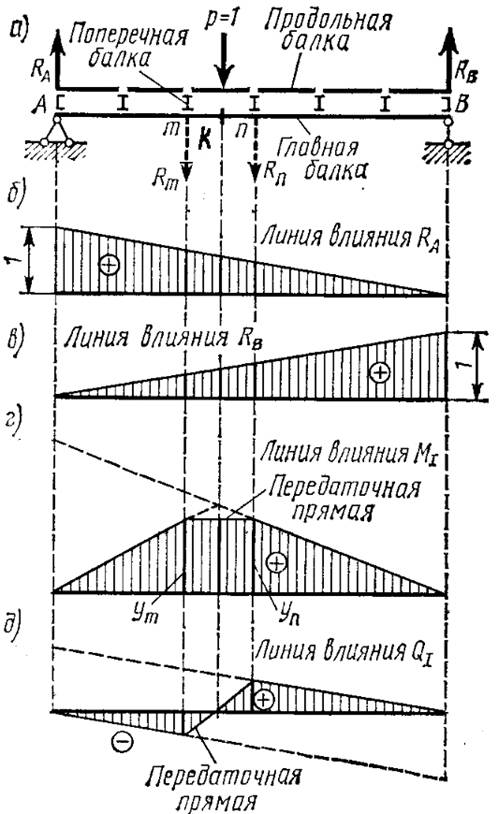
Линии влияния при узловой передаче нагрузки

Линии влияния для реакций в опорах балки Ra и Rb строятся аналогичным образом, как и для обычной простой балки.

Когда подвижная единичная сила Р=1 действует непосредственно на главную балку линии влияния внутренних усилий строятся как для обычной простой балки, что соответствует случаям, когда единичная сила находится над поперечными балками. Когда единичная сила находится между поперечными балками, линия влияния представляет собой прямую, соединяющую вершины крайних узловых ординат линии влияния рассматриваемой панели, имеющей сечение, для которого строится линия влияния – эта прямая называется передаточной прямой.

Алгоритм построения линии влияния при узловой передаче нагрузки:

1) Строится линия влияния как для обычной простой балки;

2) На построенной линии влияния ординаты под узлами панели, имеющей сечение, для которого строится линия влияния, соединяются прямой линией (передаточной прямой).

При построении линий влияния для многопролетных балок расчет начинается с балки, которой принадлежит рассматриваемое сечение, а затем переходят к остальным элементам многопролетной балки, причем усилия от единичной нагрузки могут передаваться с основных балок на вспомогательные. На вспомогательных балках линия влияния строится как при узловой передаче нагрузки. Т.е. для многопролетных балок вначале строится линия влияния для балки, в которой находится рассматриваемое сечение, а затем построенная линия влияния продолжается для всех балок вспомогательных к балке с сечением (для вспомогательных линия влияния проводится через ноль на нейтральной оси под шарнирными опорами).

Пример задачи с решением.

С. Задача 5

Построить линии влияния внутренних усилий для многопролетной балки.

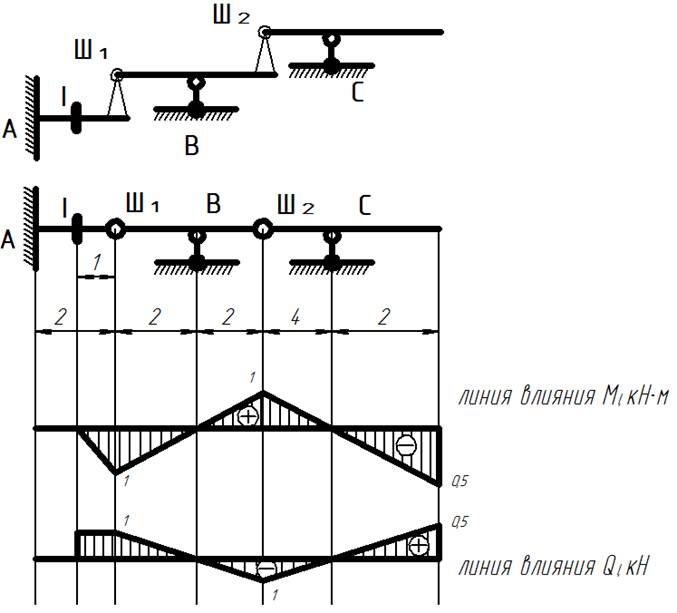
Линии влияния для многопролетной балки

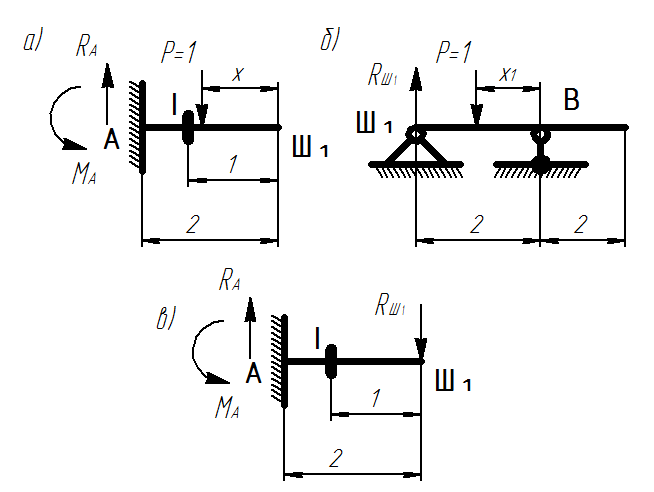
Схемы для построения линий влияния

1) Определяем реакции в опорах балки с сечением I (рис. а):

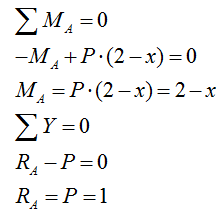
2) Рассматриваем случай расположения силы Р=1 справа от сечения I:

Рассматриваем характерные точки: x=0; 1.

При этом рассматриваем действие сил, лежащих левее сечения I.

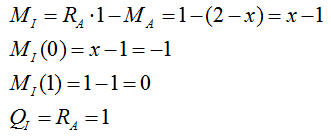
3) Рассматриваем случай расположения силы Р=1 слева от сечения I:

Рассматриваем характерные точки: x=1; 2.

При этом рассматриваем действие сил, лежащих правее сечения I.

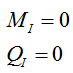
4) Определяем реакцию в шарнире вспомогательной балки Ш₁B, примыкающем к балке с сечением (рис. б):

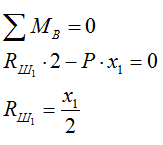
5) Определяем реакции в опорах балки с сечением I с учетом реакции Rш₁ (которую переносим на балку с сечением, меняя направление) (рис. в):

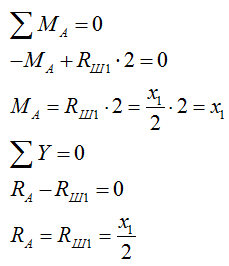
6) Рассматриваем случай расположения силы Р=1 на вспомогательной балке (справа от сечения I):

Рассматриваем характерные точки: x₁=0; 2; -2.

При этом рассматриваем действие сил, лежащих левее сечения I.

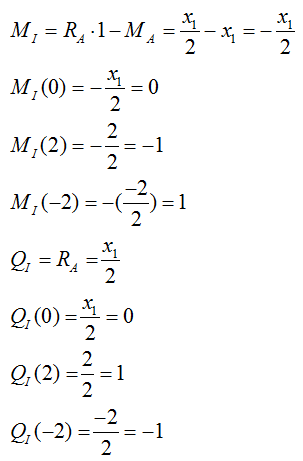
Далее расчет ведется по аналогии на базе пунктов 4-6 (рассматриваем расположение силы Р=1 на вспомогательной балке Ш₂С).

С. Задача 6

Построить линии влияния внутренних усилий для многопролетной балки.

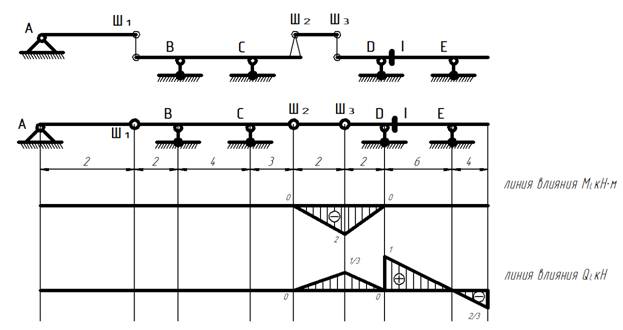
Линии влияния для многопролетной балки

Линия влияния для балки с сечением строится как показано в примерах выше.

Линии влияния для вспомогательных балок имеют значение 0 в опорах. И могут быть построены графически. Значения на линиях влияния определяются из условия подобия треугольников:

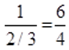
С. Задача. Метод матриц

Построить эпюры внутренних усилий и линии влияния для указанного сеченияметодом матриц.

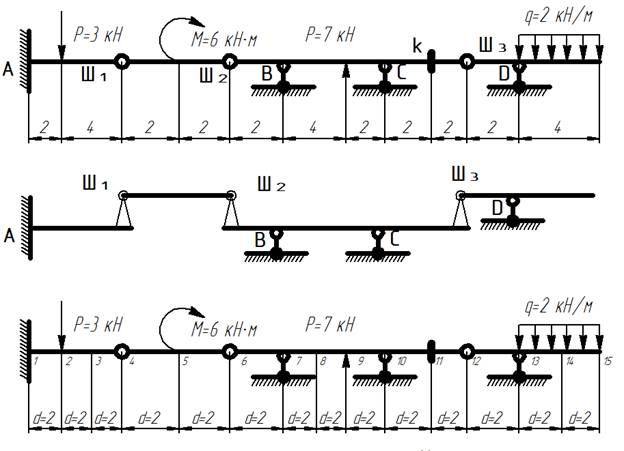
Расчет многопролетной балки методом матриц

1) Разбиваем балку на равные участки и пронумеруем их границы. При этом точки разбиения балки должны приходится на точки приложения внешних нагрузок, связей в балке.

2) Рассчитываем сосредоточенные силы в каждой точке. Для этого каждый участок рассматриваем как отдельную балку и определяем для нее реакции от внешних нагрузок. На границе двух участков суммируем реакции, направляя полученный результат в противоположную сторону, и определяем сосредоточенную силу в точке на границе двух участков.

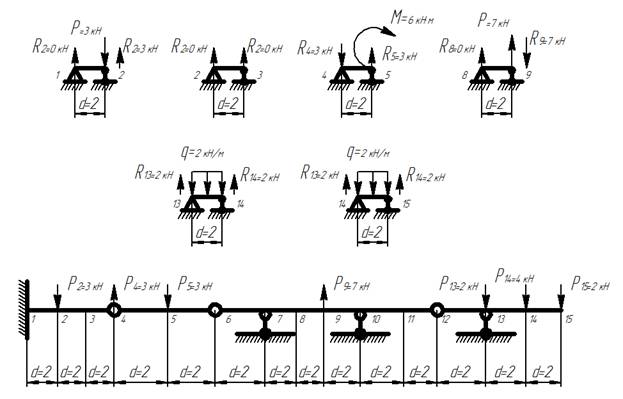
Расчет сосредоточенных сил

3) Составляем матрицу нагрузки Р (положительное направление принимаем для силы, направленной вниз):

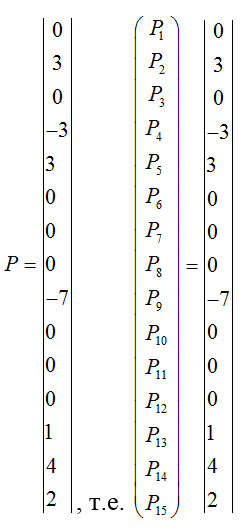
4) Построим эпюры изгибающих моментов для многопролетной балки для случаев нахождения силы Р=1 в каждой введенной точке.

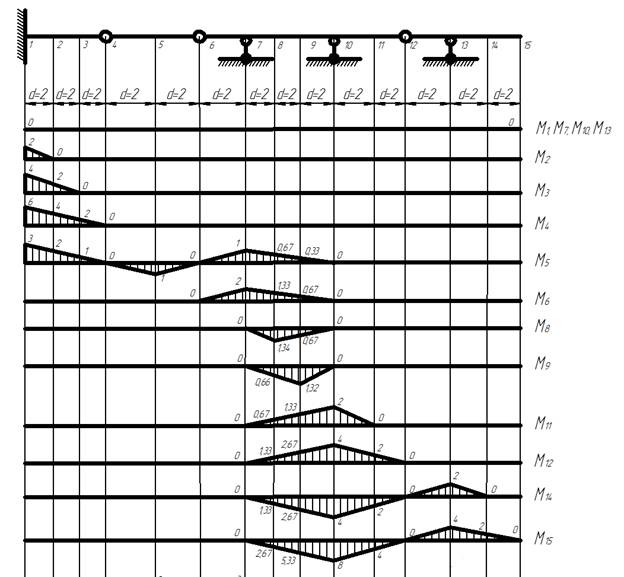
Эпюры изгибающих моментов от силы Р=1

5) Составляем матрицу влияния моментов L_M, каждый столбец которой представляет собой ординаты построенных эпюр изгибающих моментов в введенных точках:

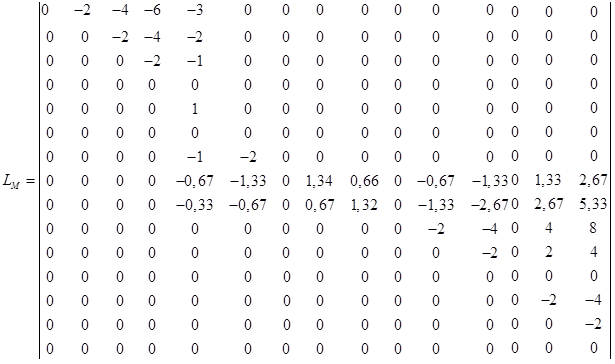
, т.е.:

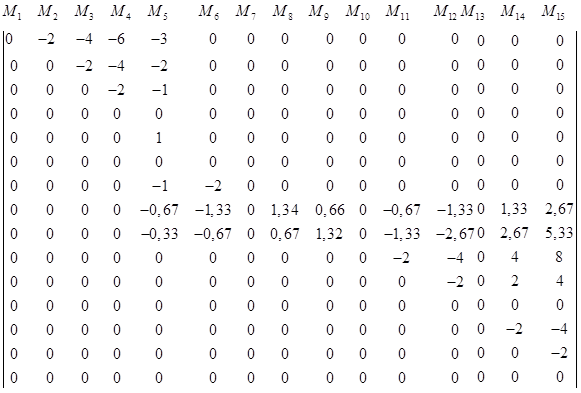
6) Составляем матрицу влияния поперечных сил L_Q. Для этого воспользуемся матрицей перехода K_QM от матрицы L_M к L_Q.

Матрица K_QM имеет туже размерность, что и матрица L_M (в данном примере 15×15).

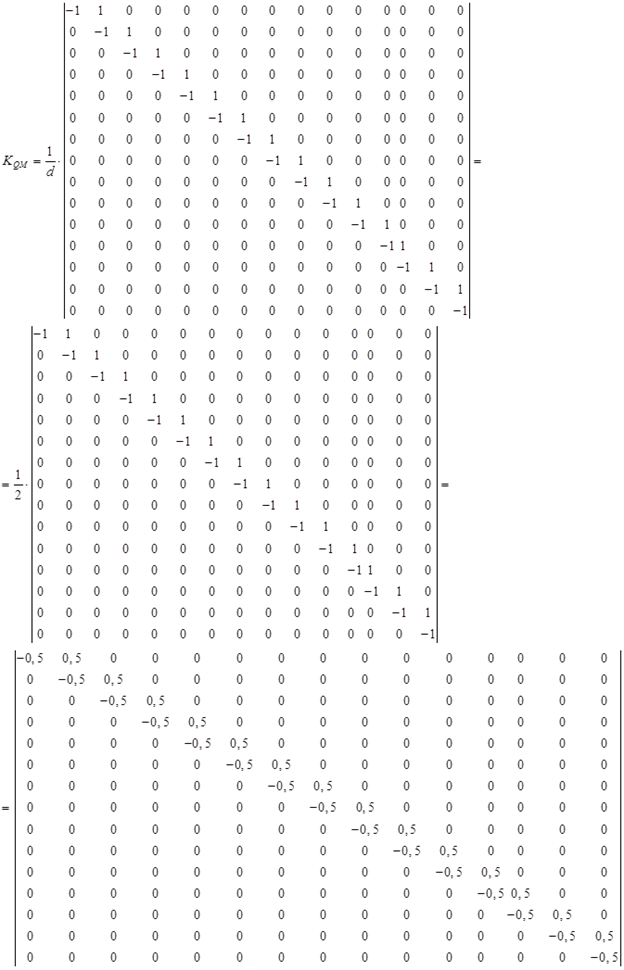
где d – длина участков, на которые разбита многопролетная балка.

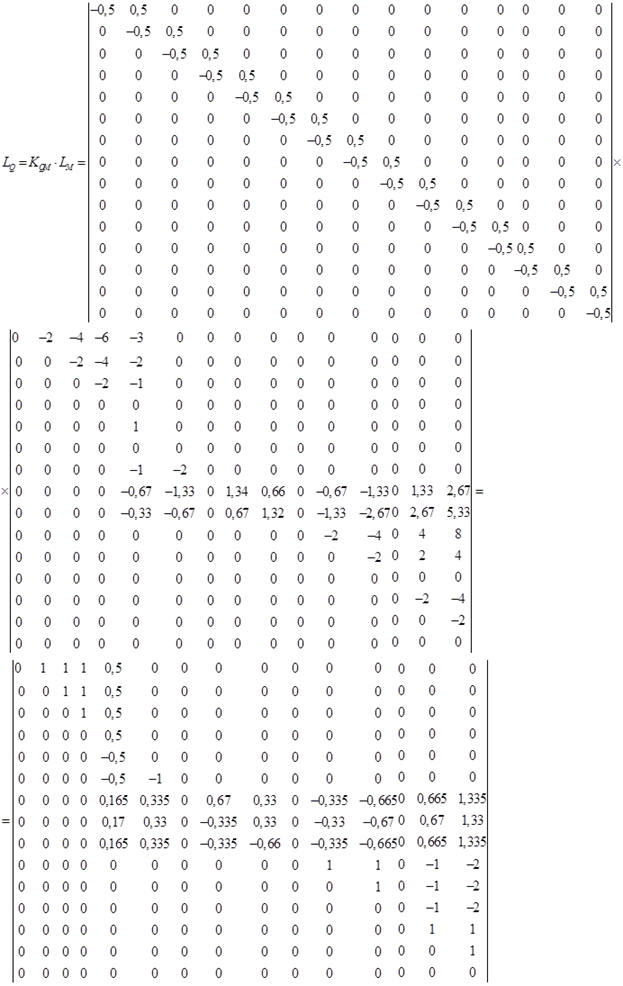
7) Составляем матрицу изгибающих моментов М:

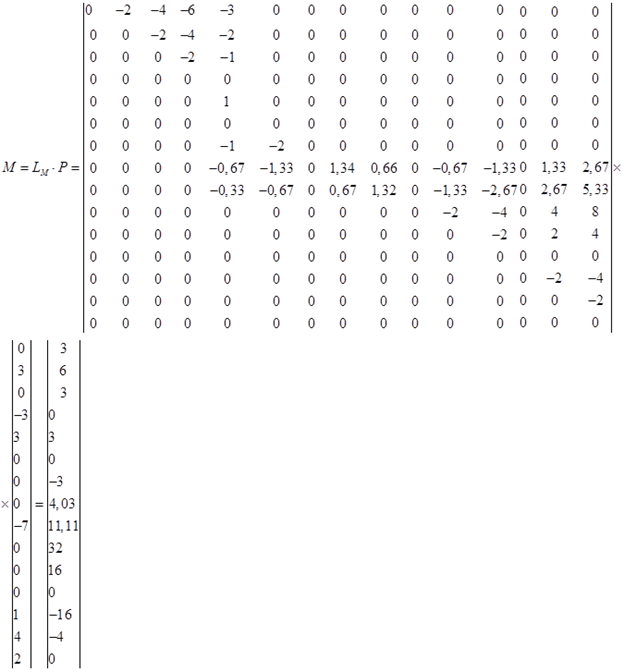
8) Составляем матрицу поперечных сил Q:

9) Строим эпюры изгибающих моментов М и поперечных сил Q. Для этого полученные величины матриц М и Q откладываем в введенных точках. При этом для участка с распределенного нагрузкой необходимо значения эпюры, построенной из матрицы, сложить с эпюрой от распределенной нагрузки в пределах каждого участка с распределенного нагрузкой, рассматривая этот участок как самостоятельную балку на опорах (рисунок 1). При построении эпюр учитываем, что под сосредоточенным моментом должен быть скачок на его величину на эпюре изгибающих моментов, а на эпюре поперечных сил его быть не должно.

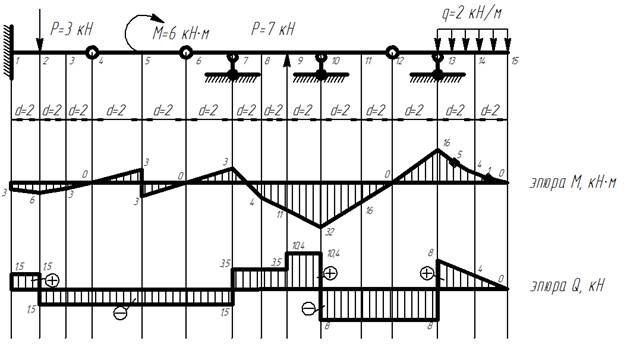
Эпюры внутренних усилий

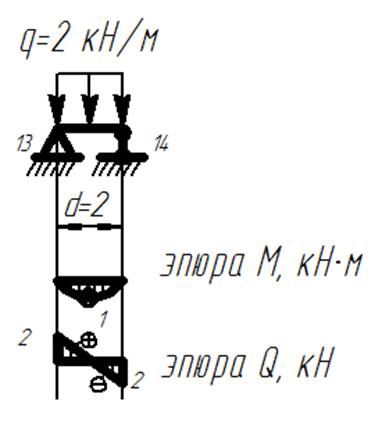
Рисунок 1. Эпюры внутренних усилий для участка с распределенной нагрузкой

10) Построение линий влияния изгибающего момента М и поперечной силы Q.

Каждая строка матриц L_M и L_Q содержит ординаты линии влияния для соответствующего сечения, проходящего через введенную точку.

Заданному сечению, находящемуся в 11 введенной точке соответствуют 11 строки матриц L_M и L_Q.

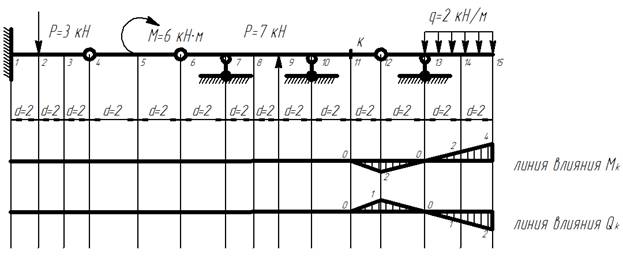
Линии влияния для сечения k

11) Определяем изгибающий момент М и поперечную силу Q в сечении k по линиям влияния:

- изгибающий момент М_k:

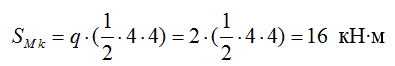
- поперечная сила Q_k:

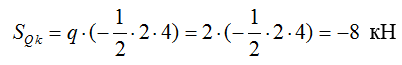
Полученные значения соответствуют значениям на эпюрах в сечении.

Расчет рам

Принципы расчет простой рамы аналогичен расчету простой балки. Единственным отличием является появление горизонтальных реакций в опорах даже от вертикальных нагрузок.

Количество степеней свободы плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:

W = 3Д – 2Ш – С₀

При W=0–система неизменяема и статически определима (т.е. может быть решена путем составления уравнений равновесия).

Для определения реакций в опорах применяетсяпринцип освобождения от связей – систему можно освободить от связей, если эти связи (например, опоры) заменить реакциями. Далее составив уравнения равновесия для новой полученной системы определяют величины введенных реакций.

Уравнения равновесия для плоской системы можно составить в следующих видах:

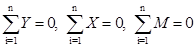
В элементах стержневой системы на плоскости могут возникать три вида внутренних усилий: продольная сила N,поперечная сила Q, изгибающий момент M. Положительные значения указанных усилий в зависимости от направления внутренних усилий определяются как на рис. 1:

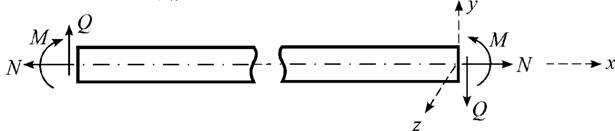
Рисунок 1. Правило знаков для внутренних усилий

Правила для проверки правильности построения эпюр:

1. На участках стержня, на которые действует равномерно распределенная нагрузка q эпюра изгибающих моментов М имеет вид выпуклой (вогнутой) кривой (выпуклость это кривой направлена в ту сторону, куда и направлена распределенная нагрузка), эпюра Q – наклонной прямой.

2. В местах расположения на стержне сосредоточенной силы P на эпюре поперечной силы Q всегда будет перепад на величину этой сосредоточенной силы. В месте расположениясосредоточенного момента на эпюре изгибающих моментов М также всегда будет перепад на величину этого сосредоточенного момента.

Расчет составной рамы

Составные рамы представляют собой статически определимые геометрически неизменяемые распорные системы. Характерной особенностью распорных систем является наличие горизонтальных составляющих опорных реакций при действии вертикальной нагрузки. Для определения реакций в таких системах составляют два уравнения моментов относительно опорных шарниров и два – относительно ключевого шарнира. Проверкой правильности нахождения реакций служат уравнения равновесия – сумма проекций всех сил на оси X и Y.

При составлении уравнений относительно ключевого шарнира рассматриваются отдельно левая и правая части рама, разделенные ключевым шарниром.

Если составную раму можно разделить на основную – статически определимую геометрически неизменяемую раму, и вспомогательную (приставную) раму, прикрепленную к основной при помощи шарнира, то ее расчленяют на отдельные рамы по шарниру, вместо которого прикладывают два неизвестных усилия (горизонтальное и вертикальное), причем расчет начинают вести со вспомогательной (приставной) рамы.

С. Задача 1

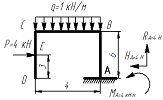
Построить эпюры внутренних усилий для простой рамы.

Подробнее: С. Задача 1

С. Задача 2

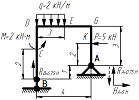
Построить эпюры внутренних усилий для простой рамы.

С. Задача 1

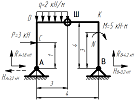
Построить эпюры внутренних усилий для составной рамы.

Данную раму разделить на основную (статически определимую и геометрически неизменяемую) и вспомогательную нельзя. Поэтому рассчитываем ее как неделимую систему.

Подробнее: С. Задача 1

С. Задача 1

Построить эпюры внутренних усилий для простой рамы.

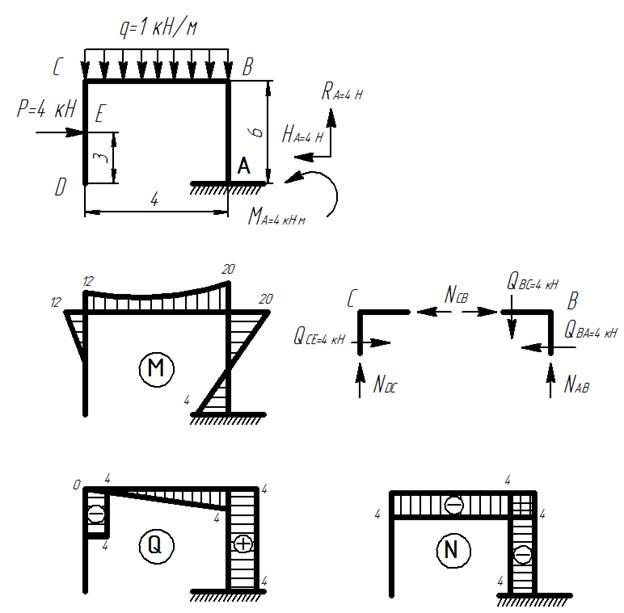
Простая рама

1) Определяем реакции в опорах:

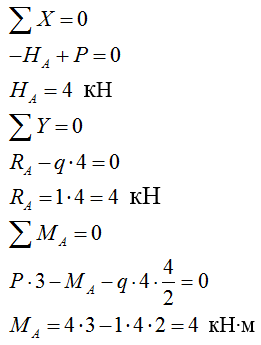
2) Строим эпюру изгибающих моментов М (построение ведем с любого "свободного" конца рамы):

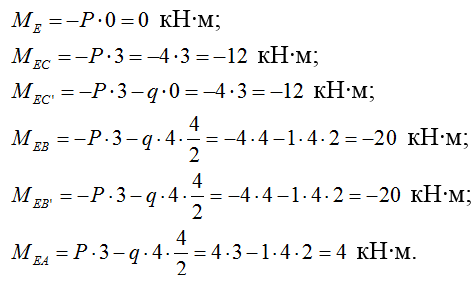
3) Строим эпюру поперечных сил Q (формула Журавского):

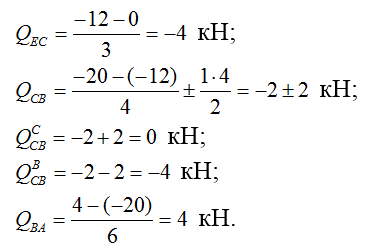
4) Строим эпюру продольных сил N методом вырезания узлов:

Рассматриваем узел С:

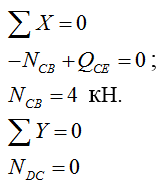
Рассматриваем узел B:

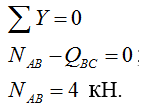
С. Задача 2

Построить эпюры внутренних усилий для простой рамы.

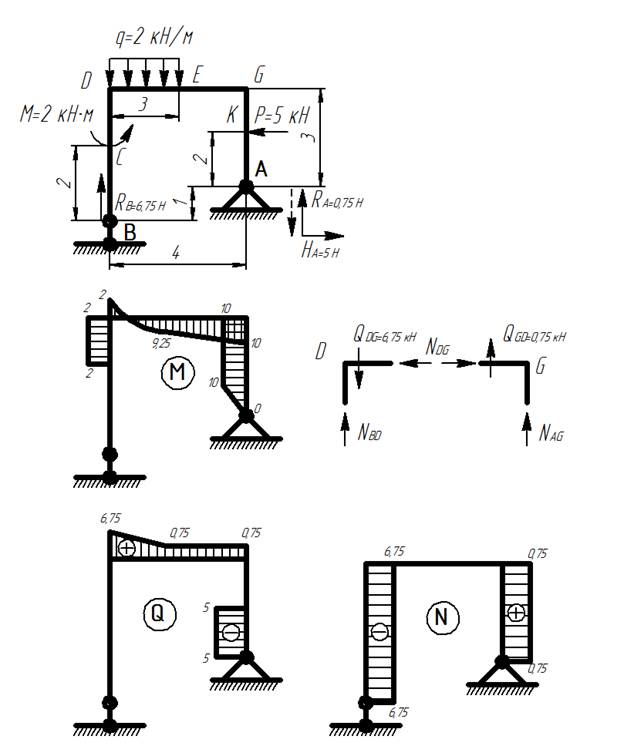
Простая рама

1) Определяем реакции в опорах:

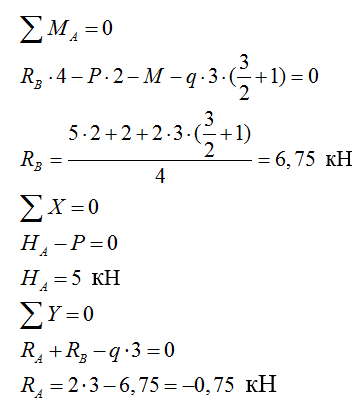
2) Строим эпюру изгибающих моментов М:

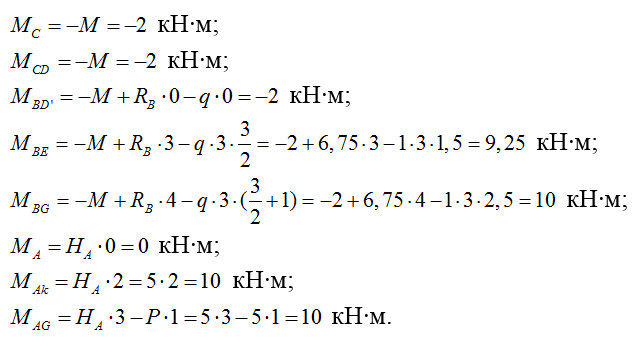
3) Строим эпюру поперечных сил Q:

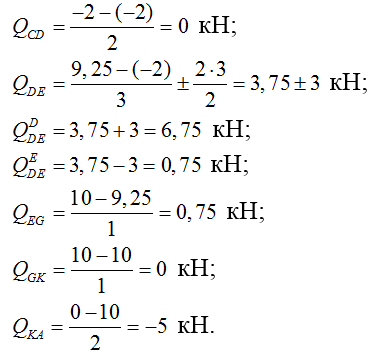
4) Строим эпюру продольных сил N:

Рассматриваем узел D:

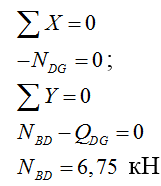
Рассматриваем узел G:

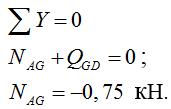
С. Задача 3

Построить эпюры внутренних усилий для простой рамы.

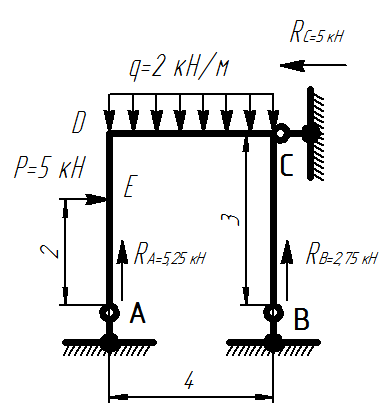
Простая рама

1) Определяем реакции в опорах:

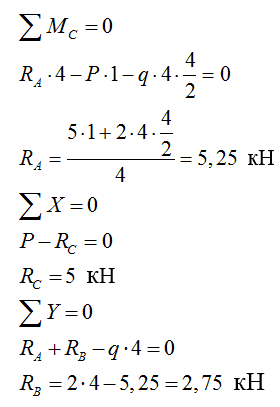
Проверка:

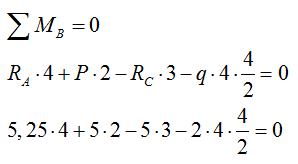
2) Строим эпюру изгибающих моментов М:

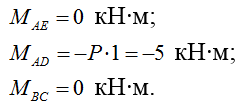
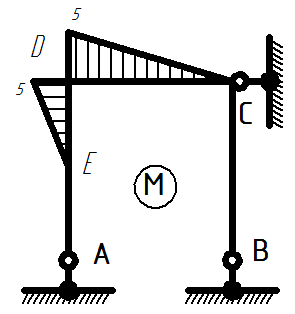
Эпюра изгибающих моментов

3) Строим эпюру поперечных сил Q:

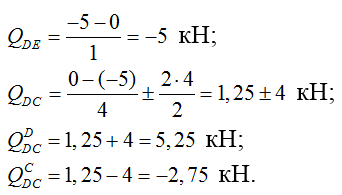
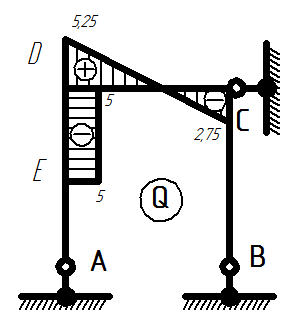
Эпюра поперечных сил

4) Строим эпюру продольных сил N:

Рассматриваем узел D:

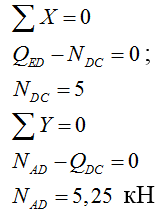
Рассматриваем узел G:

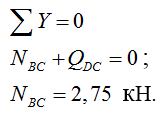
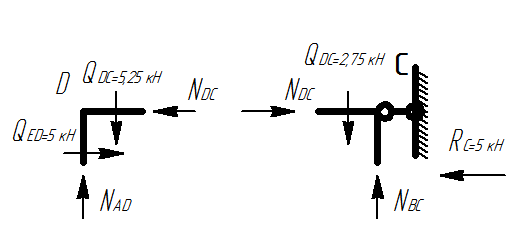
Метод вырезания узлов

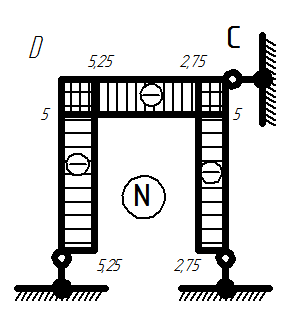
Эпюра продольных сил

С. Задача 4

Построить эпюры внутренних усилий для простой рамы.

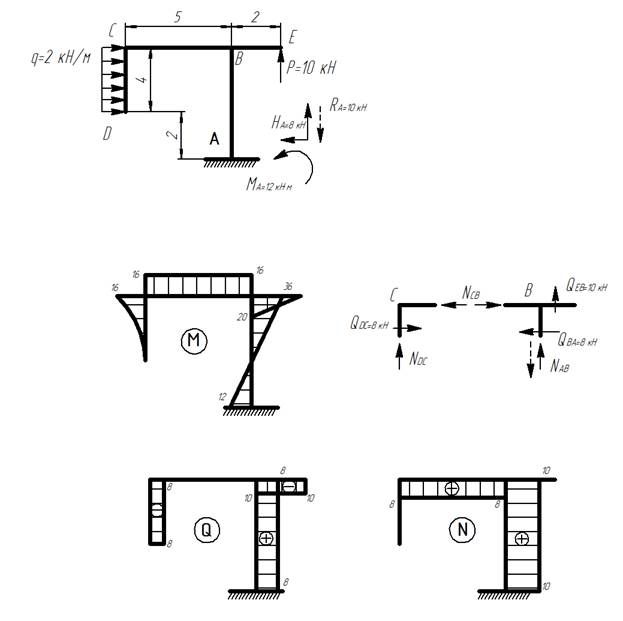
Простая рама

1) Определяем реакции в опорах:

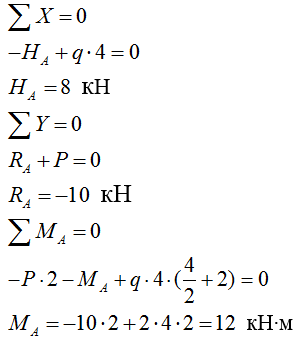
2) Строим эпюру изгибающих моментов М:

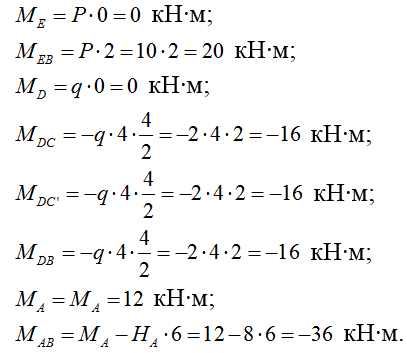
3) Строим эпюру поперечных сил Q:

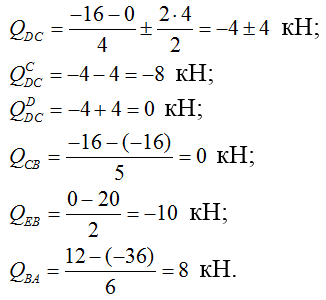
4) Строим эпюру продольных сил N:

Рассматриваем узел D:

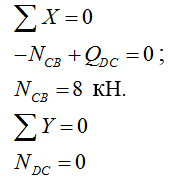
Рассматриваем узел G: