Уравнения плоского движения твердого тела

Плоским называется такое движением твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Из определения следует, что траектории всех точек тела находятся в параллельных плоскостях, которые в свою очередь, параллельны одной и той же неподвижной плоскости. Примером такого движения может служить движение книги по плоскости стола. Все точки, лежащие на страницах книги, движутся в параллельных плоскостях, которые в свою очередь параллельны плоскости стола. Другой пример - колесо, которое катится по прямолинейному рельсу. Траектории всех точек колеса лежат в параллельных плоскостях.

Плоское движение твердого тела имеет большое значение в технике, так как звенья многих механизмов и машин совершают движения этого вида. Рассмотрим в качестве примера кривошипно-шатунный механизм (рис. 11.1).

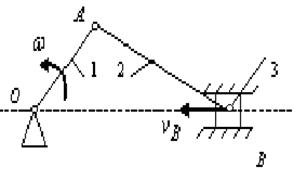
Рис. 11.1

Звено 1 – кривошип совершает вращательное движение; звено 2 – шатун совершает плоское движение; звено 3 – ползун совершает поступательное движение.

При изучении плоского движения, как и любого другого, необходимо рассмотреть способы задания этого движения, а также приемы вычисления скоростей и ускорений точек тела.

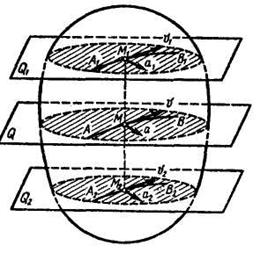
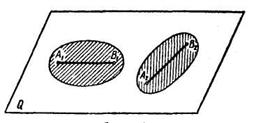
Рис. 11.2 Рис. 11.3

Рассмотрим движение точек тела, расположенных на одном пер­пендикуляре к неподвижной плоскости Q. Точка М₁ движется в плоскости Q_,1 , а точка М₂ — в плоскости Q₂; обе плоскости параллельны непод­вижной плоскости Q (рис. 11.2).

При движении тела отрезок M₁M₂ остается перпендикулярным плоскости Q, т. е. остается параллельным своему начальному положению. Это значит, что все точки этого перпендикуляра, аналогично точкам тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометри­чески равные скорости и ускорения, т. е. траектории A₁B₁ , А₂В₂, АВ точек тела M₁, M₂, М тождественны и параллельны, их скорости 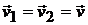и ускорения 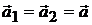также равны.

Основываясь на этом свойстве плоского движения твердого тела, устанавливаем, что движение каждой точки плоской фигуры в непод­вижной плоскости Q определяет собой движение всех точек твердого тела, расположенных на перпендикуляре к плоскости Q, восставленном в этой точке.Это позволяет свести изучение плоского движения твер­дого тела к изучению движения плоской фигуры в ее плоскости.

Так как положение плоской фигуры на плоскости вполне определяется положением двух ее точек или положением отрезка, соединяющего две точки этой фигуры (рис. 11.3), тo движение плоской фигуры в ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости.

Предположим, что плоская фигура переместилась на плоскости из положения I в положение II (рис. 11.4). Отметим два положения отрезка АВ, принадлежащего фигуре. Покажем, что перемещение фигуры можно осуществить совокуп­ностью двух перемещений: поступательного перемещения и поворота.

1-й вариант. Переместим фигуру поступательно из положения АВ в положение A₁В’, т. е. так, чтобы точка А переместилась в новое положение А₁, а точка В описала траекторию, тождественную траектории точки А. Затем повернем фигуру вокруг точки А₁ на угол φ₁ так, чтобы точка В' совпала с точкой В₁.

2-й вариант. Переместим фигуру поступательно из положения АВ положение А'В₁, a затем повернем ее вокруг точки В₁ на угол φ₂ так, чтобы точка А' совпала с точкой А₁.

Вариантов перемещений может быть столько, сколько точек плоской фигуры, т.е. бесчисленное множество.

Как видно, поступательное перемещение плоской фигуры различно в различных вариантах, а угол поворота и направление поворота одинаковы:

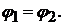(11.1)

Из этого следует, что всякое непоступательное перемещение плоской фигуры в ее плоскости можно рассматривать как совокупность двух перемещений: поступательногоперемещения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг полюса.

При этом поступательное перемещение зависит от выбора полюса, числовая величина угла поворота и направление поворота от выбора полюса не зависят.

Из вышеизложенного следует, что действительное движение плоской фигуры в ее плоскости в каждый момент времени можно рассматривать как совокупность поступательного движения и вращения. Поступательная часть движения фигуры зависит от выбора полюса и определяется его движением.

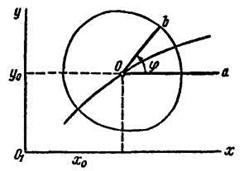
Рис. 11.4 Рис. 11.5

Приняв за полюс некоторую точку О и обозначив 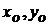ее коорди­наты в неподвижной системе хО₁у (рис. 11.5), можно определить движение полюса О, а следовательно, и поступательное движение всей фигуры уравнениями 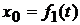и .

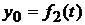Для получения угла, характеризующего вращательную часть движения плоской фигуры, проведем через полюс О две полупрямые Оа и Ob, из которых Оа не принадлежит плоской фигуре и движется поступательно вместе с полюсом О, a Ob принадлежит этой фигуре и вместе с ней вращается вокруг полюса О.

Обозначив 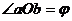, можно определить вращательное движение фигуры уравнением вращения 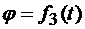. Таким образом, движение плоской фигуры в ее плоскости, а следовательно, и движение всего тела определяются тремя уравнениями, называемыми уравнениями плоского движения твердого тела:

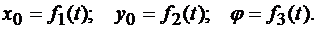(11.2)

Пример 1.Колесо радиуса R = 0,4 м катится по прямолинейному горизонтальному рельсу с постоянной угловой скоро­стью 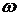= 2 рад/с (рис. 11.6). Записать уравнения плоского движения колеса, если центр колеса имеет постоянную скорость: 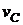= 0,8 м/с.

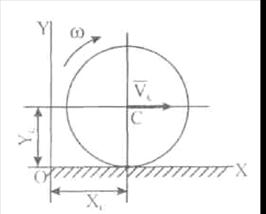
Рис. 11.6

Решение. Так как колесо движется равномерно, то координа­та центра колеса по оси х будет равна:

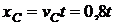м.

Координата центра колеса по оси у постоянна и равна радиусу:

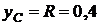м.

Угол поворота колеса при равномерном вращении равен:

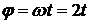рад.

Ответ. 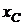= 0,8t м; 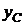= 0,4 м; 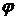= 2t рад.