Скорость и ускорение точки при координатном
способе задания движения
Определение скорости точки
Определим модуль и направление скорости точки по уравнениям ее движения в декартовых координатах. Пусть заданы уравнения движения точки (рис. 8.11):
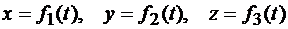 .
.
Обозначим орты осей координат 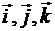 . Проведем из начала координат О в движущуюся точку М радиус-вектор
. Проведем из начала координат О в движущуюся точку М радиус-вектор 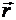 . Согласно рис. 6,
. Согласно рис. 6,
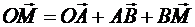 или
или 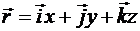 .
.
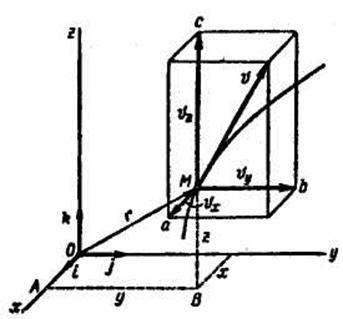
Рис. 8.11
Скорость точки равна производной от радиуса-вектора по времени. Найдем эту производную, учитывая, что орты 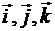 имеют неизменные модули и направления, т. е. постоянны и могут быть вынесены за знак производной:
имеют неизменные модули и направления, т. е. постоянны и могут быть вынесены за знак производной:
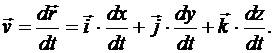
Построив прямоугольный параллелепипед, ребра которого параллельны осям координат, а диагональ совпадает со скоростью 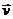 , получим проекции скорости
, получим проекции скорости 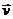 на оси координат
на оси координат 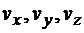 равные алгебраическим величинам отрезков Мα, Мb, Мс.
равные алгебраическим величинам отрезков Мα, Мb, Мс.
Тогда разложение скорости на компоненты по осям координат примет вид
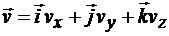 .
.
Сопоставляя обе формулы, определяющие скорость, находим:
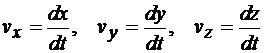 .
.
Следовательно, проекции скорости точки на неподвижные оси декартовых координат равны первым производным от соответствующих координат точки по времени.
Пользуясь принятым обозначением производных по времени, имеем:
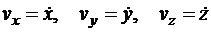 .
.
Вычислив проекции скорости на оси декартовых координат, можно определить модуль и направление скорости точки по следующим формулам:
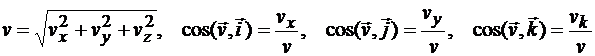 .
.
Движение точки в плоскости хОу (рис. 8.12) задается двумя уравнениями движения:
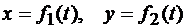 .
.
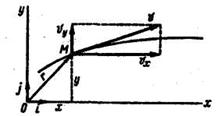
Рис. 8.12
Модуль и направление скорости точки в этом случае определяются так
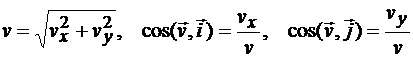 .
.
Прямолинейное движение точки задается одним уравнением (рис. 8.13)
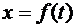 .
.
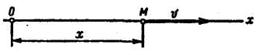
Рис. 8.13
В этом случае модуль скорости точки равен абсолютной величине проекции скорости на ось х:
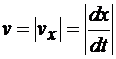 .
.
При 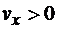 точка движется по направлению оси х (рис. 8.13), при
точка движется по направлению оси х (рис. 8.13), при 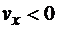 - противоположно направлению оси.
- противоположно направлению оси.
Определение ускорения точки
Определим модуль и направление ускорения точки по уравнениям ее движения в декартовых координатах.
Пусть заданы уравнения движения точки (рис. 8.14)
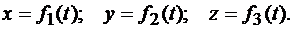
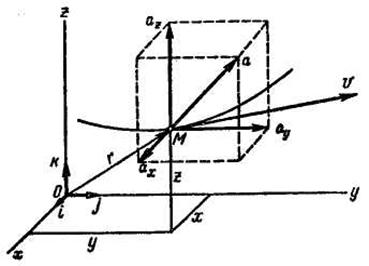
Рис. 8.14
Радиус-вектор 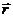 движущейся точки М представим в виде
движущейся точки М представим в виде
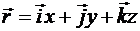 .
.
Так как ускорение точки равно второй производной от радиуса-вектора по времени, а векторы 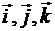 постоянны, то имеем
постоянны, то имеем
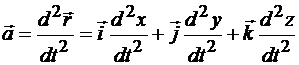 .
.
Разложим ускорение 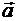 на составляющие по осям координат:
на составляющие по осям координат:
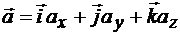 ,
,
где 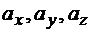 - проекции ускорения
- проекции ускорения 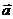 на оси х, y,z.
на оси х, y,z.
Сопоставляя обе формулы, определяющие ускорение, получаем:
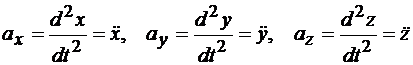 .
.
Так как первые производные от координат точки по времени равны проекциям скорости на соответствующие оси, т.е. 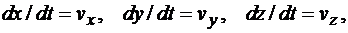 то проекции ускорения точки можно представить в другом виде:
то проекции ускорения точки можно представить в другом виде:
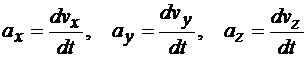 .
.
Таким образом, проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствующих координат точки по времени или первым производным по времени от проекций скорости на соответствующие оси.
Вычислив проекции ускорения на координатные оси, можно определить модуль и направление ускорения точки по следующим формулам:

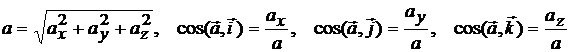 .
.
Движение точки в плоскости хОу задается двумя уравнениями движения:
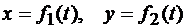 .
.
Модуль и направление ускорения точки в этом случае (рис. 8.15) определяются так:
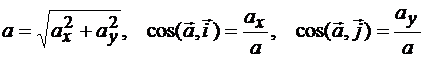 .
.
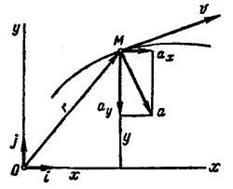

Рис. 8.15 Рис. 8.16
Прямолинейное движение точки задается одним уравнением х 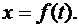 . В этом случае модуль ускорения
. В этом случае модуль ускорения 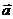 равен абсолютному значению его проекции на ось х, т. е.
равен абсолютному значению его проекции на ось х, т. е.
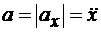 .
.
Ускорение 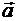 направлено в сторону оси х, если
направлено в сторону оси х, если 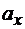 >0 (рис. 8.16), в противоположно оси х, если
>0 (рис. 8.16), в противоположно оси х, если 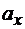 < 0.
< 0.
Пример 1.Движение точки задано уравнениями: 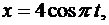 см;
см; 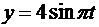 , см. Найти траекторию точки в координатной форме и задать движение точки в векторной форме (рис. 8.17).
, см. Найти траекторию точки в координатной форме и задать движение точки в векторной форме (рис. 8.17).
Решение. Исключим время из уравнений движения. Для этого возведем обе части заданных уравнений в квадрат и сложим их:
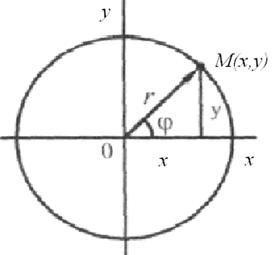
Рис. 8.17
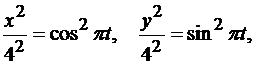
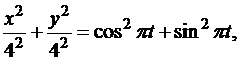
или
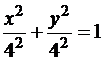 .
.
Траектория — окружность радиуса 4 см.
Для получения радиуса-вектора используем формулу (6):
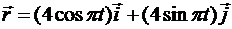 .
.
Пример 2.Движение точки задано уравнениями 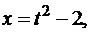 см;
см; 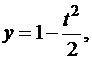 см. Найти траекторию точки в координатной форме (рис. 8.18).
см. Найти траекторию точки в координатной форме (рис. 8.18).
Решение. Преобразуем уравнения движения:
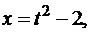
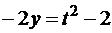 .
.
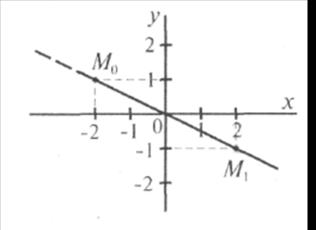
Рис. 8.18
Получим уравнение траектории х = -2у (рис. 8.18). Установим границы траектории. Начало движения в точке 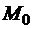 :
:
при  ,
,
при 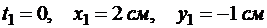 ,
,
при 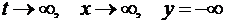 .
.
Ответ. Траекторией точки будет полупрямая, ограниченная точкой М (-2,1).
Пример 1.Автомобиль движется по плоской кривой по закону 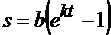 , где b и k – постоянные. Ускорение автомобиля во время движения составляет угол 60о с касательной к траектории.
, где b и k – постоянные. Ускорение автомобиля во время движения составляет угол 60о с касательной к траектории.
Найти скорость и ускорение автомобиля и радиус кривизны траектории.
Решение. Для нахождения скорости и касательного ускорения точки вычисляем первую и вторую производную от пути по времени:
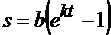 , (1)
, (1)
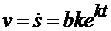 , (2)
, (2)
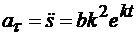 . (3)
. (3)
Зная скорость точки, можем получить выражение нормального ускорения точки:
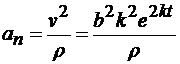 . (4)
. (4)
Для нахождения ρ воспользуемся постоянным углом между ускорением и его касательным ускорением:
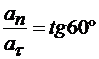 . (5)
. (5)
Подставив вместо 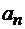 и
и 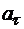 соответствующие им значения из выражений (3) и (4), получим
соответствующие им значения из выражений (3) и (4), получим
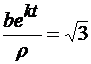 . (6)
. (6)
Следовательно,
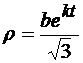 . (7)
. (7)
Полное ускорение
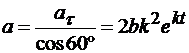 . (8)
. (8)
Перейдем к переменной s. Для этого уравнение (1) перепишем в следующем виде:
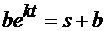 . (9)
. (9)
Подставляя (9) в (2), (7) и (8), получаем
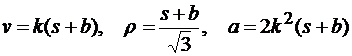 .
.
Пример 2. Точка М движется в плоскости хОу согласно уравнениям:
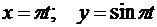 ,
,
где х, у — в сантиметрах; t — в секундах.
Определить траекторию, скорость и ускорение точки, а также радиус кривизны траектории для момента времени 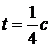 .
.
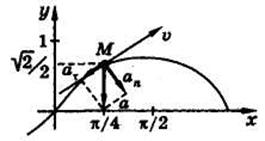
Рис. 1.2.1
Решение. Для определения траектории точки исключим из уравнений движения время: 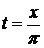 , тогда у = sin х. Траектория точки — синусоида (рис. 1.2.1).
, тогда у = sin х. Траектория точки — синусоида (рис. 1.2.1).
Определим положение точки на траектории. Имеем при
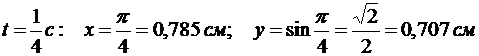
— точка М на траектории.
Получим проекции скорости точки на оси координат, дифференцируя координаты по времени:
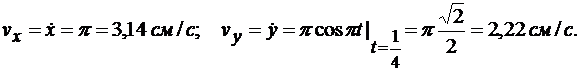
По найденным проекциям определим модуль скорости
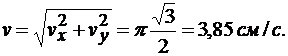
Определим проекции ускорения точки на оси координат, дифференцируя проекции скорости:
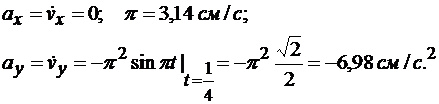
Модуль ускорения точки
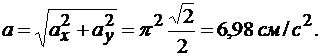
В соответствии с величинами проекций скорости и ускорения изобразим их на рис. 1.2.1.
Поскольку точка описывает криволинейную траекторию, то ее ускорение можно представить в виде векторной суммы двух составляющих: 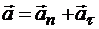 , где
, где 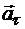 — касательное ускорение,
— касательное ускорение, 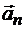 — нормальное ускорение точки.
— нормальное ускорение точки.
Вектор 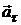 направлен по касательной, то есть по одной линии со скоростью; вектор
направлен по касательной, то есть по одной линии со скоростью; вектор 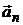 направлен по главной нормали (перпендикулярно касательной) и всегда внутрь траектории.
направлен по главной нормали (перпендикулярно касательной) и всегда внутрь траектории.
Модуль касательного ускорения равен
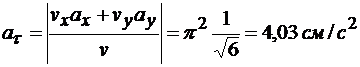 .
.
В данном случае направления векторов 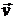 и
и 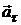 противоположны (рис. 1.2.1), поэтому движение точки замедленное.
противоположны (рис. 1.2.1), поэтому движение точки замедленное.
Так как векторы 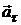 и
и 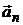 всегда взаимно перпендикулярны, то модуль полного ускорения точки равен
всегда взаимно перпендикулярны, то модуль полного ускорения точки равен 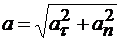 .
.
Отсюда находим модуль нормального ускорения
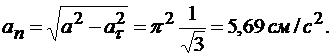
Радиус кривизны траектории определяем из формулы для нормального ускорения 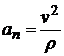 , а именно:
, а именно:
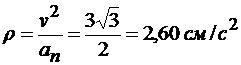 .
.
Пример 3. Точка М движется на плоскости по окружности радиуса R = 10 см согласно уравнению
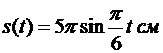 .
.
Найти положение точки на траектории, а также скорость и ускорение точки в момент времени t = 7 с.
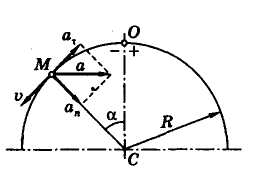
Рис. 1.2.2
Решение. При задании движения точки естественным способом должны быть известны ее траектория, начало отсчета, положительное направление дуговой координаты, а также уравнение движения точки по траектории s(t).
Выберем в качестве начала отсчета верхнюю точку окружности и положительное направление — по часовой стрелке.
При t = 7 с положение точки М на траектории (рис. 1.2.2) определяется величиной дуговой координаты
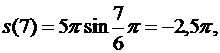
что соответствует углу 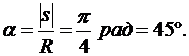
При естественном способе задания движения точки ее скорость определяется выражением 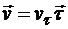 , где
, где 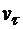 — проекция скорости на касательную, которая равна производной по времени от дуговой координаты
— проекция скорости на касательную, которая равна производной по времени от дуговой координаты 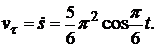
При t = 7 с получаем 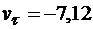 см/с, и модуль скорости равен v = 7,12 см/с.
см/с, и модуль скорости равен v = 7,12 см/с.
Знак «минус» у величины 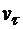 означает, что точка движется в сторону убывания дуговой координаты s(t), то есть в сторону ее отрицательных значений.
означает, что точка движется в сторону убывания дуговой координаты s(t), то есть в сторону ее отрицательных значений.
Ускорение точки является векторной суммой двух его составляющих: 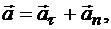 где
где 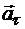 — касательное ускорение,
— касательное ускорение, 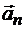 — нормальное ускорение.
— нормальное ускорение.
Направление вектора 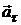 определяется знаком величины
определяется знаком величины 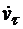 , вектор
, вектор 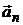 всегда направлен перпендикулярно касательной внутрь траектории. Проекция ускорения точки на касательную равна
всегда направлен перпендикулярно касательной внутрь траектории. Проекция ускорения точки на касательную равна
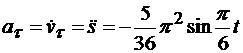 .
.
При t = 7 с получаем 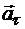 = 2,15 см/с2.
= 2,15 см/с2.
Знаки 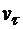 и
и 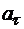 различны, поэтому движение точки по траектории в данный момент времени является замедленным.
различны, поэтому движение точки по траектории в данный момент времени является замедленным.
Модуль нормального ускорения равен
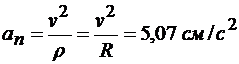 .
.
Модуль полного ускорения точки:
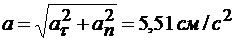 .
.
Векторы 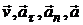 показаны на рис. 1.2.2.
показаны на рис. 1.2.2.
Пример 1. Точка М движется по своей траектории согласно уравнениям
х = t2 см; у = sin πt см. (6.4)
Определить траекторию точки М, ее скорость и ускорение в момент времени t1 = 1,5 с. Определить тангенциальное и нормальное ускорения, а также радиус кривизны траектории.
Решение. Для определения траектории точки М исключим из уравнений движения (6.4) время, после чего получим уравнение траектории в виде
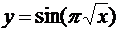
Определяем положение точки М в момент времени t1 (рис. 6.3)
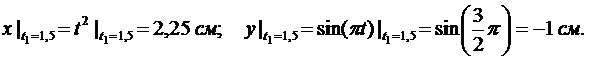
Для определения скорости точки М вычисляем первые производные от координат по времени, равные проекциям скорости точки на соответствующие оси координат:
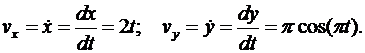 .
.
Модуль скорости определяем по формуле
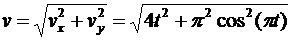 .
.
Вычисляем проекции вектора скорости точки на оси координат и её модуль в момент времени t1
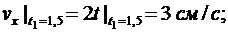
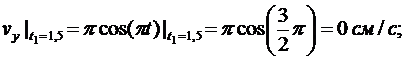
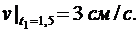
Направление вектора скорости определяем при помощи направляющих косинусов
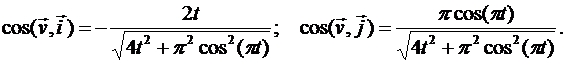
В момент времени t1 направляющие косинусы вектора скорости
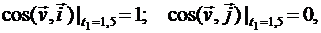
т.е. вектор скорости точки направлен параллельно оси Ох.
Для определения ускорения точки М вычисляем первые производные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствующие оси координат:
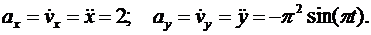 .
.
Модуль ускорения определяем по формуле
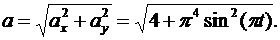
Проводим вычисления для момента времени t1
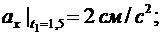
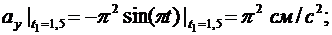
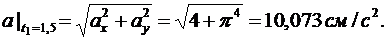
Направление вектора ускорения определяем при помощи направляющих косинусов
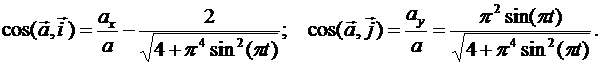
В момент времени t1 направляющие косинусы вектора ускорения
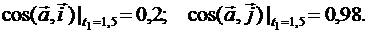
Для определения тангенциального ускорения 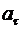 точки М учтем, что его можно определить как проекцию вектора полного ускорения на направление касательной к траектории
точки М учтем, что его можно определить как проекцию вектора полного ускорения на направление касательной к траектории
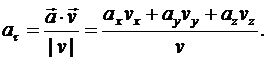 .
.
В момент времени t1
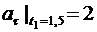 м/с2.
м/с2.
Для определения нормальной составляющей вектора полного ускорения воспользуемся формулой
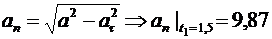 м/с2.
м/с2.
В данной задаче вектор тангенциального ускорения совпадает с проекцией вектора полного ускорения на ось Ох, а вектор нормального ускорения - с проекцией ускорения на ось Оу.
Радиус кривизны траектории определяем, используя формулу для вычисления нормального ускорения
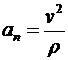 .
.
В момент времени t1
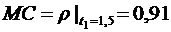 м.
м.
Изображаем все найденные величины на рис. 6.3.
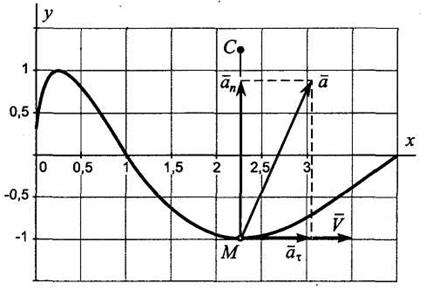
Рис. 6.3
Пример 2. Колесо радиуса r = 1 м катится без проскальзывания по горизонтальной направляющей, оставаясь в вертикальной плоскости. Центр колеса движется с постоянной скоростью v0 = 1 м/c. Составить уравнения движения точки М обода колеса, если в начальный момент времени точка находилась на оси Оу выше центра колеса. Определить тангенциальную и нормальную составляющие ускорения точки М, а также радиус кривизны траектории точки М в момент времени t1=π/2 с.
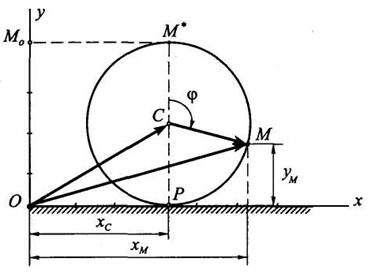
Рис. 6.4
Решение. Положение точки М определяется радиус-вектором ОМ, для которого можно записать следующее соотношение (рис. 6.4):
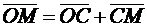 .
.
Для составления уравнений движения точки М найдем проекции вектора 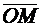 на оси декартовой системы координат xOy
на оси декартовой системы координат xOy
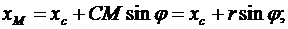
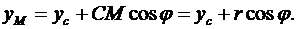
Поскольку центр колеса движется с постоянной скоростью по горизонтальной плоскости, то закон его движения можно записать в виде
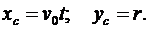
Кроме того, учтем, что при качении колеса по горизонтальной плоскости без проскальзывания выполняется условие
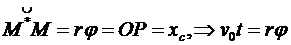 .
.
Отсюда находим
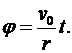
Производные
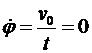 (6.5)
(6.5)
Есть угловая скорость колеса. Тогда закон движения точки М обода колеса запишем в виде
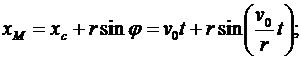
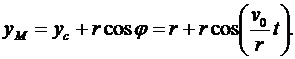
Для определения ускорения точки М вычисляем первые производные от координат по времени, равные проекциям ускорения точки на соответствующие оси координат:
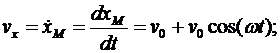
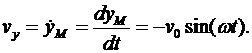
Модуль скорости определим по формуле
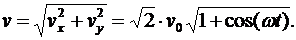
После преобразований получим
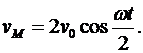
Далее представим эту формулу следующим образом
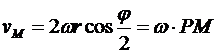 . (6.6)
. (6.6)
Из формулы (6.6) следует правило: скорость любой точки колеса равна его угловой скорости, умноженной на расстояние от этой точки дл точки касания.
В соответствии с этим скорость всех точек колеса распределяется так, как это показано на рис. 6.5.
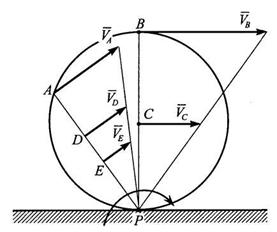
Рис. 6.5
Из этого следует еще одно правили: скорость любой точки перпендикулярна отрезку прямой, соединяющей эту точку с точкой касания.
Очевидно, что скорость точки Р при этом равна нулю.
Вычислим значение вектора скорости точки М (рис. 6.4) в момент времени t1
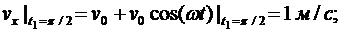
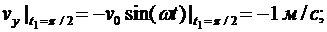
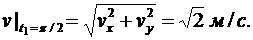
Для определения ускорения точки М вычисляем первые производные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствующие оси координат:
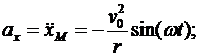 .
.
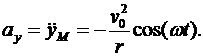
Модуль ускорения определяем по формуле
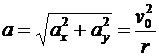 . (6.7)
. (6.7)
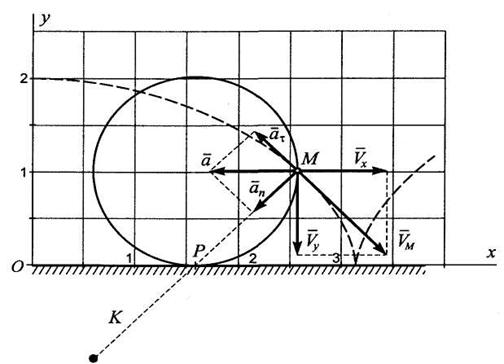
Рис. 6.6
Из формулы (6.7) следует, что величина ускорения точки зависит только от скорости центра колеса и расстояния точки от центра. Все точки, находящиеся на одинаковом расстоянии от центра, имеют одинаковые по величине ускорения. Для всех точек на окружности колеса
а = 1 м/с2.
Находим направление ускорения произвольной точки колеса. Косинус угла между ускорением и осью х найдем по известной формуле
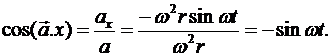
Из этой формулы следует, что ускорение любой его точки направлено к центру.
Найдем касательное и нормальное ускорение точки М. Касательное ускорение
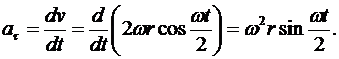 (6.8)
(6.8)
В момент времени t1
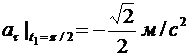 .
.
Для определения нормальной составляющей вектора полного ускорения воспользуемся соотношением
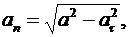
что приводит к результату
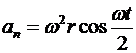 . (6.9)
. (6.9)
В момент времени t1:
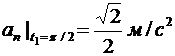 .
.
Радиус кривизны траектории определяем, используя формулу
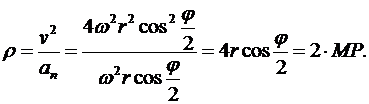 . (6.10)
. (6.10)
В момент времени t1
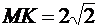 м.
м.
Таким образом, приходим к следующему выводу.
Радиус кривизны любой точки на окружности колеса равен его удвоенному расстоянию до точки касания.
Далее, представляет интерес определить касательное и нормальное ускорения и радиус кривизны точки Р (рис. 6.7). На основании соотношений (6.8)—(6.10) и с учетом того, что для точки Р угол φ=180°, находим, что для этой точки равны нулю скорость, нормальное ускорение и радиус кривизны траектории. Следовательно, ускорение точки касания колеса с плоскостью направлено по касательной к траектории. В последующих разделах данного курса будет показано, что указанное направление ускорения точки касания не зависит от углового ускорения колеса.
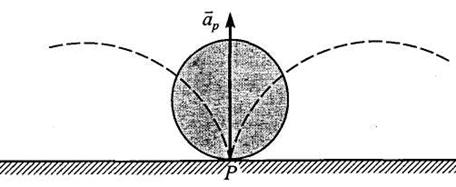
Рис. 6.7
Пример 3. Кривошип ОА кривошипно-шатунного механизма вращается с постоянной угловой скоростью ω.
Определить закон движения, траекторию, а также скорость и ускорение точки М в момент времени t1 = 0,25 с, если ОА = АВ = 15 см, AM = 5 см, ω = π рад/с. Кроме того, необходимо определить радиус кривизны траектории, тангенциальное и нормальное ускорения точки.
Решение. Для определения закона движения точки М запишем кинематическое соотношение, определяющее положение данной точки в произвольный момент времени
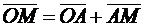 ,
,
которое в проекциях на оси декартовой системы координат примет вид
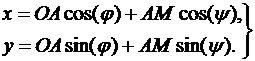 . (6.11)
. (6.11)
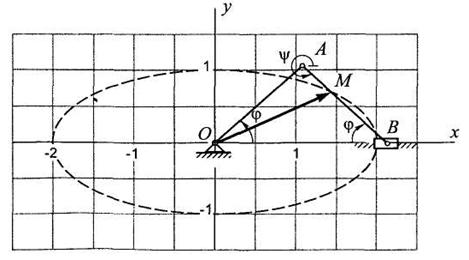
Рис. 6.8
Так как треугольник ОАВ - равнобедренный, то соотношения можно записать в виде
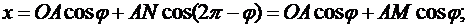
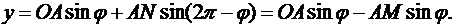
Таким образом, точка М движется по своей траектории согласно уравнениям
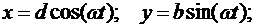 (6.12)
(6.12)
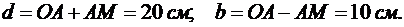
Для определения траектории точки М уравнения (6.12) представим в виде
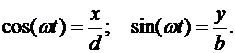
Отсюда получаем уравнение траектории
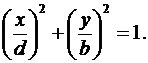 (6.13)
(6.13)
Это есть уравнение эллипса с полуосями d и b.
Определяем положение точки М в момент времени t1
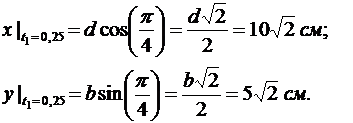
 |
Для определения скорости точки М вычисляем первые производные от координат по времени, равные проекциям скорости точки на соответствующие оси координат:
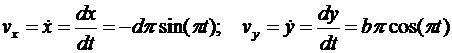 v. (6.14)
v. (6.14)
Модуль скорости определяем по формуле
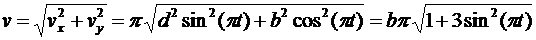 .
.
Вычисляем проекции вектора скорости и модуль скорости точки в момент времени t1
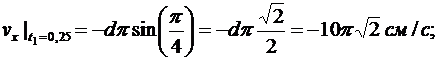
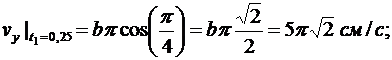
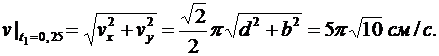
Для определения ускорения точки М вычисляем первые производные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствующие оси координат:
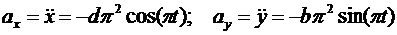 .
.
Модуль ускорения определяем по формуле
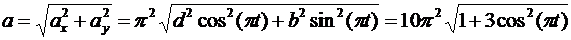 .
.
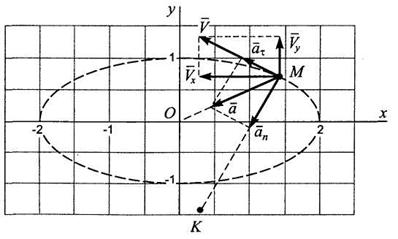
Рис. 6.9
Вычисляем значения вектора ускорения точки в момент времени t1
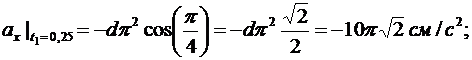
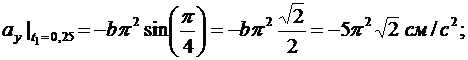
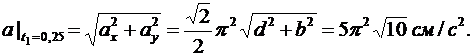
Для определения направления ускорения приведем соотношения к виду
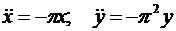 .
.
Отсюда следует, что вектор ускорения направлен в сторону, противоположную направлению радиуса-вектора точки М.
Тангенциальное ускорение точки 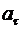 определим как производную от модуля скорости по времени
определим как производную от модуля скорости по времени
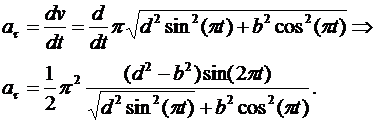
В момент времени t1
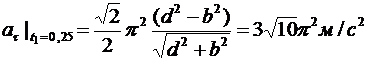 .
.
Для определения нормальной составляющей вектора полного ускорения воспользуемся соотношением
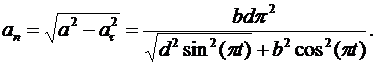
В момент времени t1
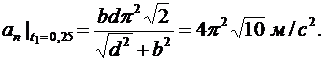
Радиус кривизны траектории определяем, используя формулу для вычисления нормального ускорения
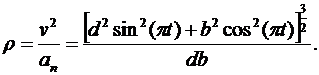
В момент времени t1
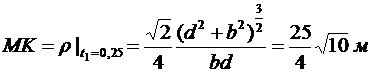 .
.
Отображаем все найденные величины на рис. 6.9.
Пример 4. Кривошип ОА кривошипно-кулисного механизма вращается с постоянной угловой скоростью 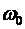 . Определить угловую скорость и угловое ускорение кулисы BD, если ω0 = π с–1, ОА = b, ОВ = 2b, b=10 см.
. Определить угловую скорость и угловое ускорение кулисы BD, если ω0 = π с–1, ОА = b, ОВ = 2b, b=10 см.
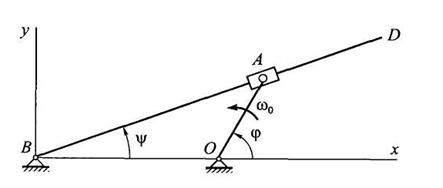
Рис. 6.10
Решение. Для определения угловой скорости и углового ускорения качающейся кулисы найдем закон ее движения, для чего запишем уравнение кинематических связей 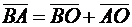 , которое в проекциях на координатные оси имеет вид:
, которое в проекциях на координатные оси имеет вид:
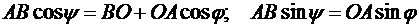 . (6.14)
. (6.14)
Разделив второе уравнение системы на первое, получим
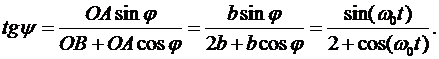
Тогда закон движения кулисы можно записать в виде
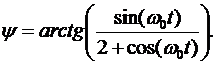
Для нахождения угловой скорости кулисы в произвольный момент времени найдем производную по времени от закона движения
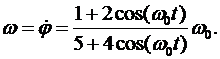
Для нахождения углового ускорения кулисы в произвольный момент времени найдем производную по времени от закона изменения угловой скорости
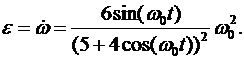
Графики изменения угла поворота ψ(t) угловой скорости ω(t) и углового ускорения ε(t) кулисы изображены на рис. 6.11
.
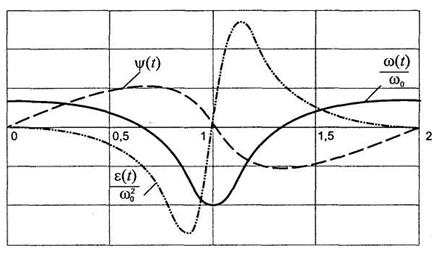
Рис. 6.11
Лекция 9
