Относительно координатных осей

Возьмем три взаимно перпендикулярные координатные оси х,у,z, которым соответствуют орты Момент силы относительно начала координат, выражается формулой

,

где 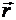- радиус-вектор точки А приложения силы относительно начала координат (рис. 3.7).

Рис. 3.7

Разложим вектор на составляющие по осям координат:

,

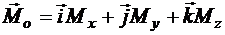где 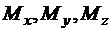- проекции 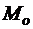на оси координат.

Из векторной алгебры известно, что векторное произведение 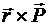можно представить определителем

,

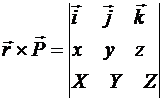где х, у, z - проекции вектора 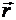, а X,Y,Z - проекции вектора на оси ко­ординат.

Приравнивая значения и определителя, разложенного по элемен­там первой строки, получаем

.

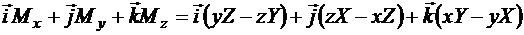Сопоставляя левые и правые части этого равенства, находим проек­ции момента на оси координат, равные моментам силы относительно этих осей:

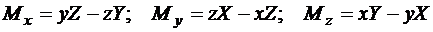. (3.3)

Формулы (3.3) называются аналитическими выражениями моментов силы относительно координатных осей.

Момент , равный геометрической сумме моментов всех сил си­стемы относительно точки О, называется главным моментом системы сил относительно этой точки (рис. 3.8):

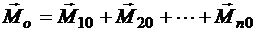. (3.4)

Рис. 3.8 Рис. 3.9

Момент, равный алгебраической сумме моментов всех сил системы относительно оси z, называется главным моментом системы сил относительно оси z (рис. 3.9):

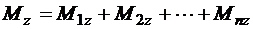. (3.5)

Главный момент системы сил относительно оси изображается отрезком, отложенным по оси z от любой ее точки О в положитель­ном направлении, если , и в отрицательном, если .

Пара сил И ЕЕ СВОЙСТВА

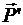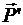Система двух равных по модулю, параллельных и противоположно направленных сил и называется парой сил. Плоскость, в которой находятся линии действия сил и , называется плоскостью действия пары сил (рис. 3.10).

Пара сил не имеет равнодействующей, силы пары не урав­новешиваются, так как они не направлены по одной прямой. Пара сил стремится произвести вращение твердого тела, к которому она приложена.

Рис. 3.10 Рис. 3.11

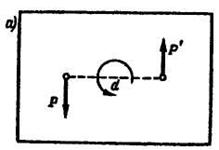
Рис. 3.12

Кратчайшее расстояние d между линиями действия сил, составляю­щих пару, называется плечом пары сил.

Действие пары сил на твердое тело характеризуется ее моментом. Момент пары сил определяется произведением модуля одной из сил пары на ее плечо:

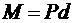. (3.6)

Если силы выражать в ньютонах, а плечо - в метрах, то момент пары сил будет выражаться в ньютон∙метрах (Н×м).

Момент пары сил изображают вектором.

Вектор момента 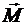пары , 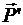направляют перпендикулярно плоскости действия пары сил в такую сторону, чтобы, смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки (рис. 3.11).

Если рассматриваются только пары сил, лежащие в одной плоскости, то эту плоскость совмещают с плоскостью чертежа (рис. 3.12).

Вместо вектора момента каждой пары сил, перпендикулярного плоскости чертежа, указывают только направление, в котором пара сил стремится вращать эту плоскость.

В этом случае момент пары сил определяют произведением модуля сил на плечо пары сил, взятым со знаком плюс или минус, т. е. момент пары сил рассматривают как алгебраическую величину

. (3.7)

Момент пары сил считают положительным, если пара сил стре­мится вращать плоскость чертежа в сторону, противоположную вра­щению часовой стрелки (рис.3.12, а), и отрицательным - в сторону вра­щения часовой стрелки(рис. 3.11, 3.12).

Свойства пар сил:

1. Две пары сил называют эквивалентными, если они обладают геометрически равными моментами, т. е. эти пары имеют одинаковые по модулю моменты, и эти моменты одинаково направлены.

2. Пару сил, не изменяя ее действия на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять ее плечо и модули сил, не изменяя числового значения величины ее момента и направления вра­щения.

3. Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, парал­лельную плоскости действия пары, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента.

Таким образом, вектор момента пары сил можно переносить в любую точку, т. е. момент пары сил является свободным вектором.

Вектор момента пары сил определяет все три ее элемента: положе­ние плоскости действия пары, направление вращения и числовое значение момента.