Формула Тейлора для многочлена

Пусть функция ƒ(х) есть многочлен Р_n(х) степени n:

ƒ(х)=Р_n(х)=а₀+а₁х+а₂х²+...+а_nхⁿ.

Преобразуем этот многочлен также в многочлен степени n относительно разности х-х₀, где х₀— произвольное число, т. е. представим Р_n(х) в виде

Р_n(х)=А₀+A₁(x-х₀)+А₂(х-х₀)²+...+А_n(х-х₀)ⁿ (26.1)

Для нахождения коэффициентов А₀, А₁ ,..., А_n продифференцируем n раз равенство (26.1):

Р'_n(х)=А₁+2А₂(х-x₀)+3A₃(x-x₀)²+...+nA_n(x-x₀)^n-1,

Р_n''(х)=2А₂+2•3А₃(х-х₀)+...+n(n-1)А_n(х-х₀)^n-2,

Р_n"'(х)=2•3А₃+2•3•4А₄(х-х₀)+...+n(n-1)(n-2)А_n(х-х₀)^n-3,

- - - - - - - - - - - - - - - - - -

Р_n⁽ⁿ⁾(х)=n(n-1)( n-2)...2•1А_n

Подставляя х=х₀ в полученные равенства и равенство (26.1), имеем:

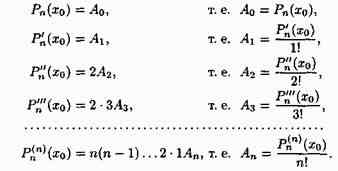
Подставляя найденные значения A₀,A₁,...,An в равенство (26.1), получим разложение многочлена n-й степени Р_n(х) по степеням (х-х0):

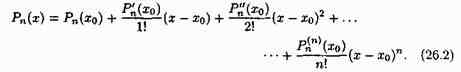
Формула (26.2) называется формулой Тейлора для многочлена Р_n(х) степени n.

<< Пример 26.1

Разложить многочлен Р(х)=-4х³+3х²-2х+1 по степеням х+1.

Решение: Здесь х₀=-1, Р'(х)=-12х²+6х-2, Р"(х)=-24х+6, Р'"(х)=-24. Поэтому Р(-1)=10, Р'(-1)=-20, Р"(-1)=30, Р'"(-1)=-24. Следовательно,

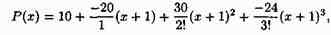
т. е. -4х³+3х²-2х+1=10-20(х+1)+15(х+1)²-4(х+1)³.

Ответ на 31 (2) вопрос :

Формула Тейлора для произвольной функции

Рассмотрим функцию у=ƒ(х). Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию ƒ(х) в виде многочлена и дать оценку погрешности этого приближения.

Теорема 26.1.Если функция ƒ(х) определена в некоторой окрестности точки х₀ и имеет в ней производные до (n+1)-го порядка включительно, то для любого х из этой окрестности найдется точка сє(х₀;х) такая, что справедлива формула

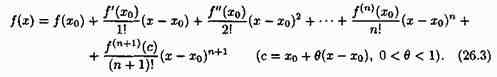
Формула (26.3) называется формулой Тейлора для функции ƒ(х). Эту формулу можно записать в виде ƒ(х)=Р_n(х)+R_n(x), где

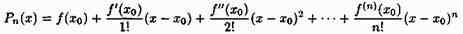
называется многочленом Тейлора, а

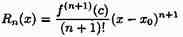
называется остаточным членом формулы Тейлора, записанным в форме Лагранжа. R_n(х) есть погрешность приближенного равенства ƒ(х)≈Р_n(х). Таким образом, формула Тейлора дает возможность заменить функцию у=ƒ(х) многочленом у=Р_n(х) с соответствующей степенью точности, равной значению остаточного члена R_n(x).

Ответ на 31 (3) вопрос:

При х₀=0 получаем частный случай формулы Тейлора — формулу Маклорена:

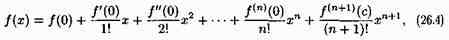
где с находится между 0 и х (с=θx, 0<θ<1).

При n=0 формула Тейлора (26.3) имеет вид ƒ(х)=ƒ(х₀)+ƒ'(с)(х-х₀) или ƒ(х)-ƒ(х₀)=ƒ'(с)(х-x₀), т. е. совпадает с формулой Лагранжа конечных приращений. Рассмотренная ранее формула для приближенных вычислений ƒ(х)≈ƒ(х₀)+ƒ'(х₀)(х-х₀) (см. «дифференциал функции») является частным случаем более точной формулы

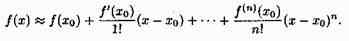
Билет №32. Формула Маклорена для e^x

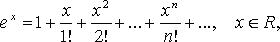
Билет №33. Формула Маклорена для sinx

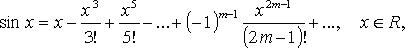
Билет №34. Формула Маклорена для cosx

Разложение функции cos x

Находим последовательно производные от f(x) = cos x.

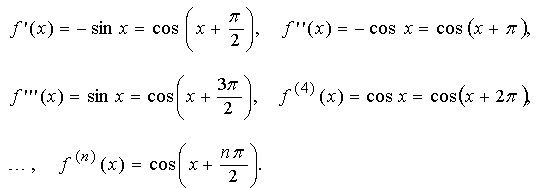
При x = 0 получаем

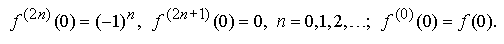
Следовательно, формула Маклорена для функции cos x имеет вид

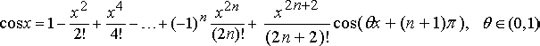
Так как 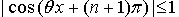, то

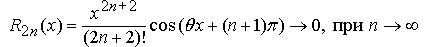
для любого фиксированного вещественного числа x. Таким образом, значения функцииcosx могут быть найдены приближенно по формуле

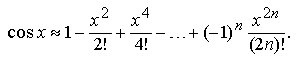
Билет №35. Формула Маклорена для ln(1+x)

 f(x)=ln (1+x). Заметим, что область определения этой функции D(y)=(–1; +∞).

Найдем формулу МакЛорена для данной функции.

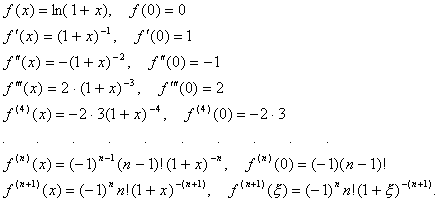
Подставим все найденные производные в ряд МакЛорена.

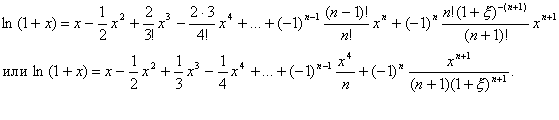
Можно доказать, что если x  (–1;1],то 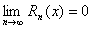, т.е. выведенная формула справедлива при x  ( –1;1].

Билет №36. Формула Маклорена для (1+х) в степени m

 f(x) = (1+x)^m, где m  R, m≠0.

При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:

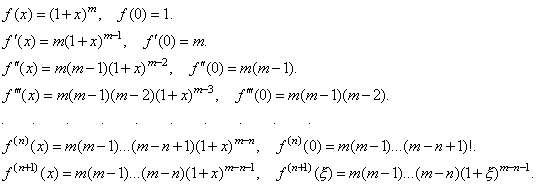
И следовательно,

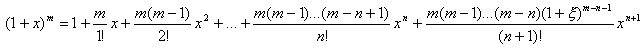Можно показать, что при |x|<1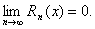

Билет № 37. Понятие функции нескольких переменных. Область определения. Частные производные первого порядка и их геометрический смысл.

Функции нескольких переменных.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).

Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

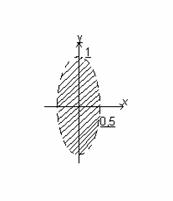
Например, функция z= 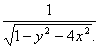задана только при 1-y 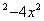>0, т.е. внутри эллипса y²+4x²<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.

Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записываетсяw=f(x,y,z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, аz=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Например, графиком функции z=4-x²-y² является параболоид.

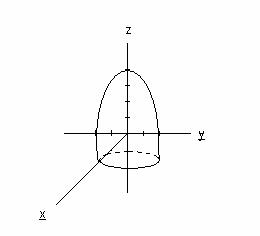
Функции трех и большего числа переменных не имеют геометрического представления.

Область определения.

Областью определения функции 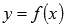(выражения f(x) ) называют множество всех значений x , для которых функция (выражение) имеет смысл.
Область определения функции 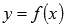обозначается как 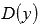или .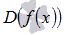

При нахождении области определения функции приходится решать различные неравенства (иррациональные, логарифмические, тригонометрические и т.п.) и системы неравенств.