Приложения определённого интеграла
Вычисление площадей плоских фигур. Пусть функция 
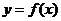непрерывна и неотрицательна на отрезке 
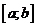. Тогда площадь 
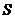под кривой 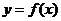на 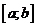численно равна определённому интегралу 
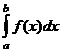, то есть
.
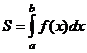Пример 14. Найти площадь фигуры (рис.1), ограниченной линиями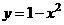 
, 
, 
, 
.
 |
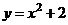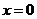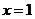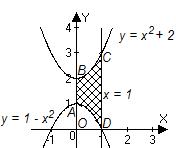Рис. 1
Решение
Фигура заключена между графиками функци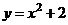й и 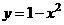. Площадь 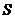находим как разность площадей
.
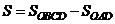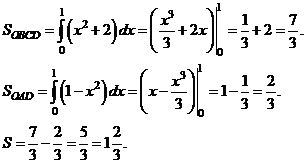
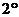Вычисление объёма тела вращения. Пусть 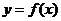- непрерывна и неотрицательна на 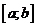(рис.2). Тогда тело, образованное вращением вокруг оси 
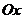криволинейной трапеции 
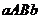, имеет объём
.
 |
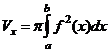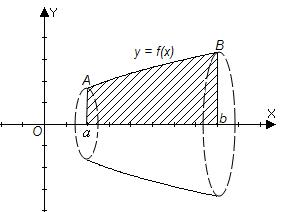Рис. 2
Пример 15. Найти объём тела (рис.3), полученного от вращения фигуры, ограниченной линиями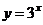 
, 
, , .
 |
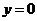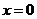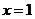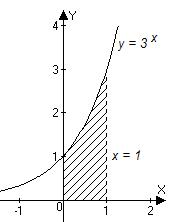Рис. 3
Решение
Искомый объём равен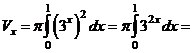 
.
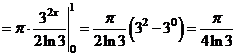Экономические приложения определённого интеграла
Пример 16. Дана функция предельных издержек
, 
,
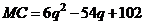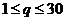где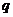 
- объём выпускаемого товара. Найти функцию издержек
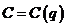
и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 30 рублей.
Решение
Известно, что предельные издержки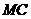 
есть производная от функции издержек 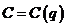, т.е. 
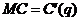. Значит, функцию издержекнаходим интегрированием
.
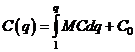Для заданной функции 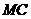имеем
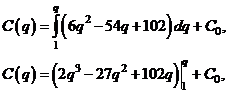
или
.
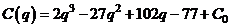Из условия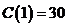 
найдём 
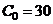. Тогда получаем,
.
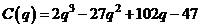При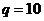 
вычислим 
.
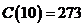Пример 17. Функция изменения затрат времени на изготовление изделий имеет вид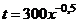 
. Найти среднее время, затраченное на освоение одного изделия в период освоения от 
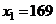до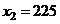 
.
Решение
Если известна функция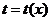 
, описывающая изменение затрат времени на изготовление изделия в зависимости от степени освоения производства, где 
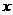- порядковый номер изделия в партии, то среднее время, затраченное на изготовление одного изделия в период освоения от 
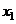до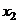 
, вычисляется с помощью интеграла
.
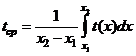В нашем случае
.
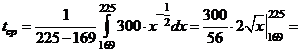
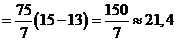Несобственные интегралы
При определении определённого интеграла предполагалось, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. Однако возможны случаи, когда одно или оба этих условия не выполняются. В этом случае соответствующие интегралы называются несобственными.
Пусть функция 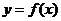интегрируема на каждом конечном отрезке 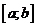, т.е. существует определённый интеграл 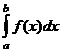. Тогда за несобственный интеграл 
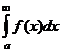принимают предел
.
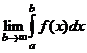Если предел существует и конечен, то говорят, что несобственный интеграл сходится. В противном случае говорят, что расходится.
Итак,
.
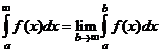Аналогично можно рассмотреть несобственный интеграл с бесконечным нижним пределом
.
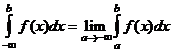Или с бесконечными верхним и нижним пределами интегрирования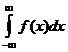 
.
.
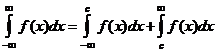Если существуют несобственные интегралы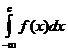 
и 
, то существует и несобственный интеграл 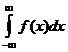, независящий от выбора промежуточной точки 
.
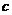Пример 18. Найти несобственные интегралы:
а)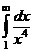 
; б) 
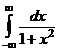; в)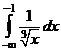 
.
Решение
а) По определению имеем
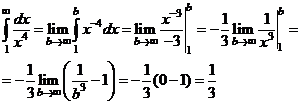
Несобственный интеграл сходится и равен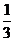 
.
б)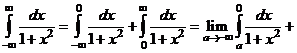 
.
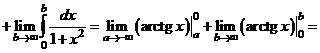
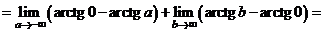
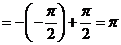Интеграл сходится.
в)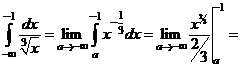 
.
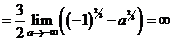Интеграл расходится.
Кроме несобственных интегралов с бесконечными пределами интегрирования в литературе рассматриваются несобственные интегралы от неограниченных функций. Предлагаем изучить этот материал самостоятельно.