Выделение основной тенденции ряда динамики.

Тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней).

Выявление тренда может проводится несколькими способами:

1. Укрупнение интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции.

2. Скользящая средняя. Суть метода в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средней ведется способом скольжения, т.е. постепенным исключением из принятого периода первого уровня и включением следующего.

Для 3–членной Ŷ_i = ;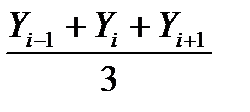

При нахождении скользящей средней по четному числу членов средняя относится к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определенной дате.

3. Аналитическое выравнивание. При этом уровни ряда выражаются в виде функции времени: .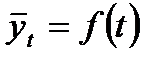

Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления. Чаще всего при выравнивании используются следующие зависимости:

Линейная f(t) = a₀ + a₁t;

Параболическая f(t) = a₀ + a₁t + a₂t² ;

Экспоненциальнaя f(t) = exp ( a₀ + a₁t).

Оценка параметров (а₀, а₁, а₂, …) осуществляется чаще методом наименьших квадратов (МНК). Так, при выравнивании ряда по прямой для нахождения параметров прямой решается система нормальных уравнений вида:

п а₀ + a₁Σt = Σу

а₀ Σt + a₁Σt² = Σt y

где п – количество уровней ряда динамики

t- условные обозначения временных уровней (t=1,2,3. . .п)

Для упрощения счета при выравнивании динамических рядов условное обозначение временных точек (t) можно вести так, чтобы Σt=0. В этом случае системы нормальных уравнений значительно упрощаются.

Так, при выравнивании по прямой система будет иметь вид:

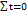
п а₀ = Σу

а₁ Σt² = Σty

При выравнивании по параболе второго порядка (если Σt=0) система имеет следующий вид:

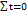
п а₀ + a₂Σt² = Σу

а₁ Σt² = Σty

а₀ Σt² + a₂Σt⁴ = Σt² y

Решая эти системы, найдем параметры трендов. В линейном тренде параметр ”а₀” означает (при данном способе обозначения t) средний уровень динамического ряда, а параметр ”a₁” – средний абсолютный прирост.

Для получения точечного прогноза в полученное уравнение тренда подставляется следующее значение t; для интервального прогноза необходимо оценить среднее квадратическое отклонение ( ):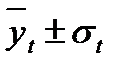

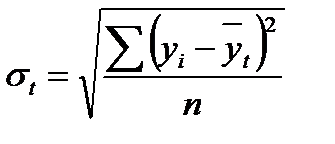
Колеблемость уровней ряда динамики от тренда можно оценить с помощью коэффициента колеблемости, рассчитываемого по формуле, который является аналогом коэффициента вариации: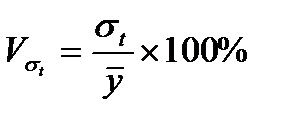

Ряды, у которых каждый уровень может быть выражен как функция предыдущих, например 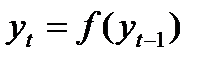, называют авторегрессионными, а зависимость между соседними членами именуют автокорреляцией и измеряют с помощью коэффициента автокорреляции.

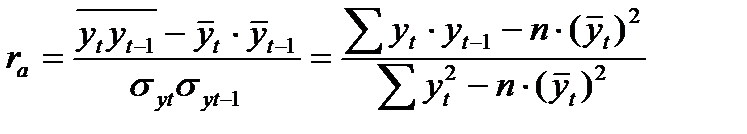
Если табличное значение коэффициента автокорреляции превышает расчетное, то автокорреляции в ряду динамики нет. Табличное значение находится по Приложению 7 в зависимости от числа уровней ряда n и уровня значимости α (чаще принимается α=0,05).

Исключение автокорреляции в рядах можно обеспечить, коррелируя не сами уровни, а так называемые остаточные величины, получаемые как разность эмпирических и теоретических (выравненных) уровней.

В свою очередь, остаточные величины (ε_t) также должны проверяться на автокорреляцию. Для этой цели может быть использован коэффициент автокорреляции для остаточных величин, а также критерий Дурбина – Ватсона (d).

,

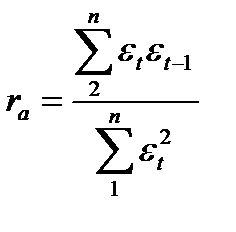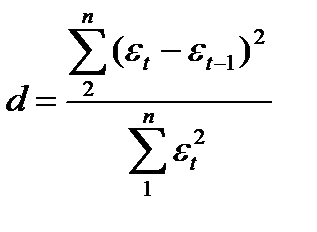
Полученное значение r_a сравнивают с табличным (см. Приложение 7) для данного числа уровней ряда (п) и при заданном уровне значимости α. Если расчетное значение меньше табличного , то можно говорить об отсутствии автокорреляции.

Подобным образом сравнивают полученное значение критерия Дурбина-Ватсона с табличными (см. Приложение 6) при заданном числе переменных в уравнении тренда (v) и числе уровней ряда (п). Превышение расчетного значения над табличными говорит об отсутствии автокорреляции.

При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. При изучении сезонных колебаний используются специальные показатели индексы сезонности I_s:

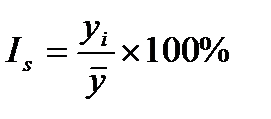
где у_i – уровни ряда;

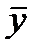- средний уровень ряда.

Однако данные одного года могут быть случайными и не отражать общей закономерности колебаний. Поэтому на практике для выявления закономерности пользуются помесячными данными за ряд лет. Тогда для каждого месяца рассчитывается средний уровень, и формула принимает следующий вид:

,

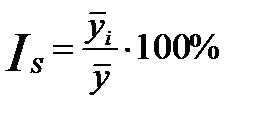где 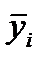- средняя для каждого месяца за 3 года;

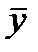- общий средний месячный уровень за 3 года.

Задание 5.

Провести анализ динамики продажи мясных консервов за 1993-1997 гг. (рассчитать абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста, средний уровень ряда, среднегодовой абсолютный прирост, среднегодовой темп роста и прироста).

годы	Консервы, млн.усл. банок
1993	891
1994	806
1995	1595
1996	1637
1997	1651
итого

Решение:

годы	Консервы, млн.усл. банок	Абсолют.приросты млн.усл.банок	Темпы роста, %	Темпы прироста, %	Абс.знач. 1% прироста, млн. усл.банок
Цеп.	Баз.	Цеп	Баз.	Цеп	Баз.
1993	891	-	0,0	-	100	-	0,0	-
1994	806	-85,0	-85,0	90,5	90,5	-9,5	-9,5	8,91
1995	1595	+789,0	+704,0	197,9	179,0	97,9	79,0	8,06
1996	1637	+42,0	+746,0	102,6	183,7	2,6	83,7	15,95
1997	1651	+14,0	+760,0	100,9	185,3	0,9	85,3	16,37
итого	6580	+760,0	-	-	-	-	-	-

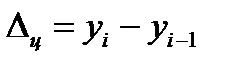Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост ( ). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле: или ,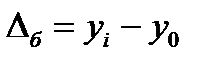

где 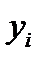- уровень i-го года;

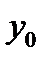- уровень базисного года.

Например, абсолютное уменьшение продажи консервов за 1994 г. по сравнению с 1993г. составило: 806 – 891= -85 млн. усл. банок (см. таблицу выше), а по сравнению с базисным 1993 г. продажа консервов в 1997 г. возросла на 760 млн. усл. банок (см. таблицу выше).

Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель принято называть темпом роста (Т_р). Он выражается в процентах, т.е.

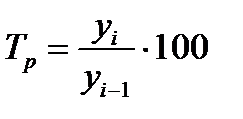или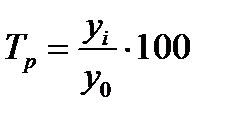

Так, для 1997 г. темп роста по сравнению с 1993 г. составил 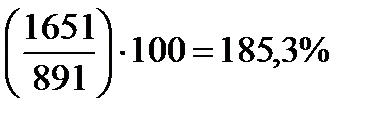(см. таблицу выше).

Темп роста может быть выражен и виде коэффициента (К_р). В этом случае он показывает, во сколько раз данный уровень ряда больше уровня базисного года или какую его часть он составляет.

Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Т_пр), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.

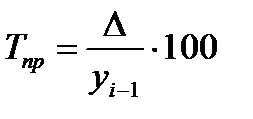или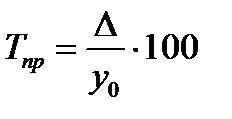

Темп прироста может быть вычислен также путем вычитания из темпов роста 100 %, т.е. Т_пр= Т_р – 100.

В нашем примере он показывает, например, насколько процентов продажа консервов в 1997 г. возросла по сравнению с 1993 г.: 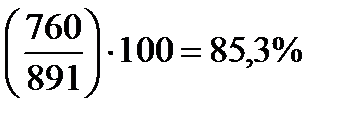, или 185,3 – 100 = 85,3%.

Показатель абсолютного значения одного процента прироста ( 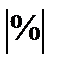) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах, т.е. 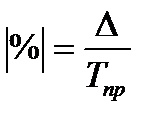или 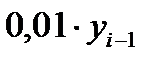. Расчет этого показателя имеет экономический смысл только на цепной основе.

Для 1997 г. абсолютное значение 1% прироста (см. таблицу выше) равно: 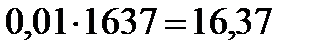млн.усл. банок.

Также необходимо рассчитать средние показатели ряда динамики, которые являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Рассчитаем следующие средние показатели:

-средний уровень ряда динамики

Так как его расчет зависит от вида ряда динамики, то определим какой ряд представлен в задании – это интервальный ряд динамики с равными периодами времени, следовательно, расчет среднего уровня ряда ( 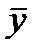) производится по формуле средней арифметической простой: .

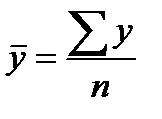В нашем примере средняя продажа мясных консервов за 5 лет составила: 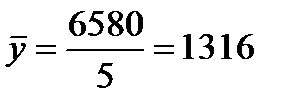млн. усл. банок.

- средний абсолютный прирост

Его определение производится по цепным абсолютным приростам по формуле: 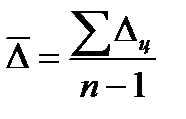или .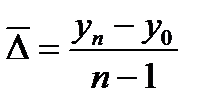

Среднегодовой абсолютный прирост продажи мясных консервов за 1993 – 1997 гг. равен: 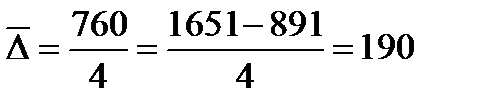млн. усл. банок.

- среднегодовой темп роста

Вычисляется по формуле средней геометрической: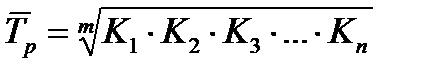

,

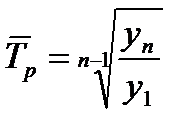где m – число коэффициентов роста.

Среднегодовой темп роста продажи мясных консервов за 1993 – 1997 гг. рассчитаем двумя способами: 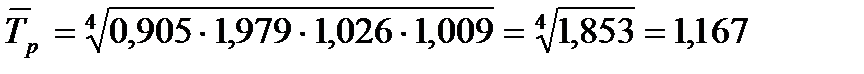или 116,7%;

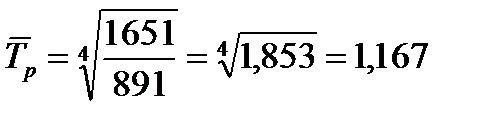или 116,7%.

- среднегодовой темп прироста

Получаем, вычтя из среднего темпа роста 100%. Т.е.: .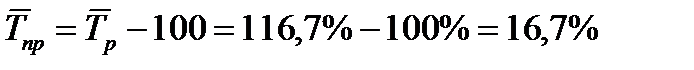

Задание 6.

На основе данных о производстве стиральных машин фирмой за 9 месяцев 1997гг. произведите сглаживание ряда методом трех- и четырехчленной скользящей средней.

Решение:

месяцы	Стир.машины, тыс. шт	3-членные скользящие суммы	3-членные скользящие средние	4-членные скользящие суммы	4-членные скользящие средние (нецентр.)	4-членные скользящие средние (центрир.)
1	155	-	-	-	-	-
2	163	-	161,7	-	154,0	-
3	167	485	153,7	-	154,8	154,4
4	131	461	152,0	616	150,8	152,8
5	158	456	145,3	619	141,5	146,2
6	147	436	145,0	603	145,0	143,3
7	130	435	140,7	566	137,5	141,3
8	145	422	134,3	580	-	-
9	128	403	-	550		-

Взяв данные за первые три месяца, исчислим трехчленные суммы, а затем скользящую среднюю: ;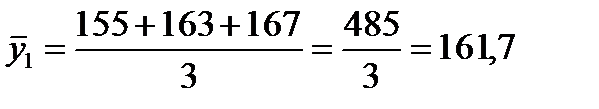

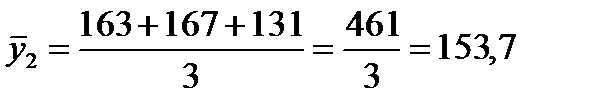и т.д.

Интервал скольжения можно также брать четный (четыре, шесть и т.д.). Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определенной дате. Например, в нашем случае (смотри таблицу) сначала находим четырехчленные суммы, затем скользящие средние нецентрированные:

;

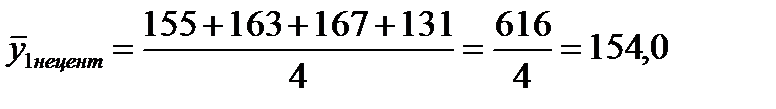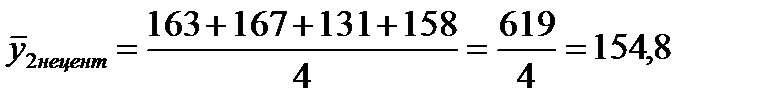и т.д.

Затем находим центрированные скользящие средние следующим образом: ;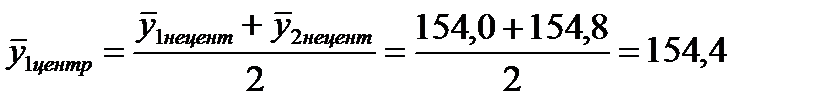

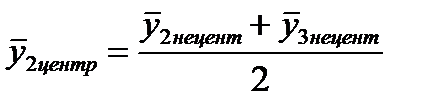и т.д.

Задание 7.

В таблице приведены данные о динамике производства молока в регионе за 1993-1997гг.:

Годы	1997	1998	1999	2000	2001	Итого
Производства молока в регионе, млн. т	13,3	13,5	14,8	16,1	16,6	74,3

Произведите аналитическое выравнивание ряда динамики по прямой. Сделайте выводы о характере общей тенденции изучаемого явления, а также точечный и интервальный прогноз на 2002 г.

Решение:

Годы	уi	t	t2	У*t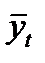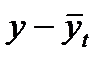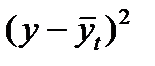
1997	13,3	-2	4	-26,6	13,02	0,28	0,08
1998	13,5	-1	1	-13,5	13,94	-0,44	0,19
1999	14,8	0	0	0	14,86	-0,0	0,00
2000	16,1	1	1	16,1	15,78	-0,32	0,10
2001	16,6	2	4	33,2	16,70	-0,1	0,01
Итого	74,3	0	10	9,2	74,30	-	0,38

Для выравнивания ряда динамики по прямой используем уравнение: .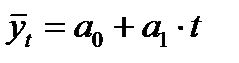

Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров 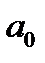и :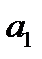

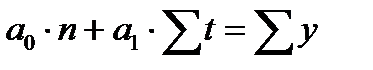
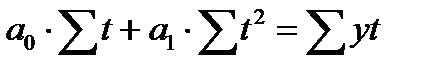
где у - исходный уровень ряда динамики,

n – число уровней ряда динамики,

t – показатель времени, который обозначается порядковыми номерами начиная с низшего. Например:

годы	1993	1994	1995	1996	1997
t	1	2	3	4	5

Однако, в некоторых случаях, для упрощения расчетов t подбирают таким образом, чтобы 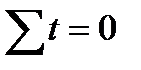и тогда последовательность значений может быть такой (обратите внимание на то, что число уровней ряда динамики нечетное – n=5):

годы	1993	1994	1995	1996	1997
t	-2	-1	0	1	2

Для расчета примем второй вариант обозначения t.

Тогда система нормальных уравнений примет следующий вид:

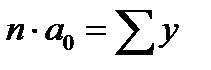
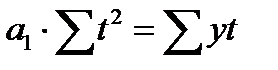
Отсюда получаем:

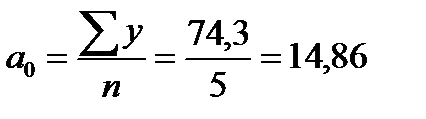
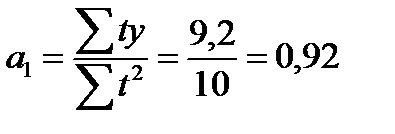
В результате получаем следующее уравнение основной тенденции производства молока в регионе за 1993 – 1997 гг.:

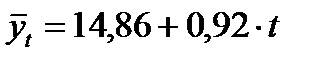
Подставляя в уравнение принятые обозначения t, вычислим выравненные уровни ряда динамики:

1993 г. -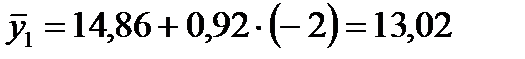

1994 г. - 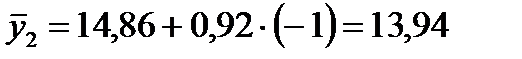и т.д. (значения 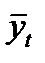приведены в расчетной таблице).

По окончании расчета в основной тенденции целесообразно построить график, на котором следует изобразить исходные данные и теоретические значения уровней ряда.

Однако если число уровней ряда четное, то условное обозначение показателя времени принимает следующий вид:

годы	1992	1993	1994	1995	1996	1997
t	-5	-3	-1	+1	+3	+5

(это означает, что счет времени ведется полугодиями).

Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно измерить по формуле:

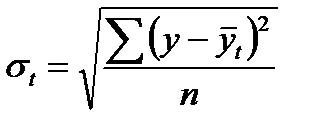- среднее квадратическое отклонение

Используя данные расчетной таблицы, рассчитаем показатель колеблемости производства молока в регионе:

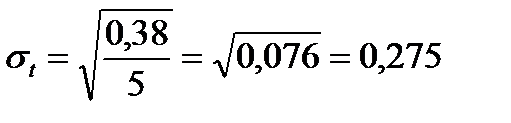млн. т.

Относительной мерой колеблемости является коэффициент вариации, который вычисляется по формуле .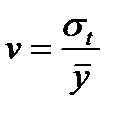

В нашем примере 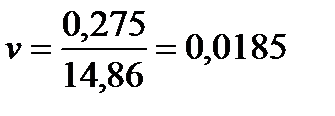или 1,85%.

Задачи для самостоятельного решения:

Задача 56.

Определить вид рядов динамики, представленных ниже:

А) данные о выпуске книг , журналов и газет в РФ (тыс.печат. единиц):

Годы
у	47,2	44,0	42,7	34,8	30,9

Б) Численность населения Вологодской области на начало года (млн.чел.)

годы
у	1,279	1,267	1,256	1,245	1,235	1,228	1,223	1,218	1,214

В) среднемесячная зарплата и выплаты социального характера в Вологодской области, в рублях за 2010г:

Месяцы	январь	март	май	июль	сентябрь	ноябрь	Декабрь
у	78,4	76,1	76,6	101,4	110,6	126,2	159,1

Г) удельный вес численности городского и сельского населения в общей численности населения на начало года, %:

Годы	Все население	В том числе
городское	Сельское

Задача 57.

Определить вид рядов динамики, характеризующих изменение следующих статистических показателей:

a) Численности населения (по состоянию на начало каждого года);

b) Численности фермерских хозяйств (по состоянию на начало каждого года);

c) Среднемесячной заработной платы работников по отраслям экономики по годам;

d) Числа родившихся по годам;

e) Денежных доходов и расходов населения по годам;

f) Индекса потребительских цен на товары и услуги населению (по месяцам за ряд лет);

g) Распределение розничного товарооборота по всем каналам реализации по формам собственного по годам;

h) Вкладов населения в учреждения Сбербанка РФ (на конец каждого года);

i) Удельного веса новой товарной продукции машиностроения в общем объеме продукции по годам.

Задача 58.

Провести анализ динамики продажи мясных консервов за 2006-2010 гг. (рассчитать абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста, средний уровень ряда, среднегодовой абсолютный прирост, среднегодовой темп роста и прироста).

годы	Консервы, млн.усл. банок	Абсолют. приросты млн.усл. банок	Коэффициенты роста	Темпы роста, %	Темпы прироста, %	Абс.значение 1% прироста, млн. усл.банок
Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.
итого

Задача 59.

Имеются следующие данные по объединению о производстве промышленной продукции за 2005-2010 гг. (в сопоставимых ценах), млн. руб.:

2005г.	2006г.	2007г.	2008г.	2009г.	2010г.
67,7	73,2	75,7	77,9	81,9	84,4

Для анализа ряда динамики определить: абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста, средние показатели динамики. Результаты расчетов представить в табличной форме.

Задача 60.

Ввод в действие жилых домов предприятиями всех форм собственности в одном из регионов в 2003-2010 гг. характеризуется следующими данными, тыс. м² общей площади:

2003г.	2004г.	2005г.	2006г.	2007г.	2008г.	2009г.	2010г.

Для анализа ряда динамики определить: 1) цепные и базисные: абсолютные приросты, темпы роста и прироста, 2) абсолютное значение одного процента прироста, среднегодовой абсолютный прирост за весь год. Результаты расчетов представить в табличной форме.

Задача 61.

Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице базисные показатели динамики по следующим данным о производстве часов в регионе за 2002-2010 гг.:

Годы	Производство часов, тыс. шт	Базисные показатели динамики
Абс.прирост, млн шт	Темп роста, %	Темп прироста,%
	55,1	-	100,0	-
		2,8
			110,3
				14,9
				17,1
			121,1
		13,5
	69,1
		14,0		25,4

Задача 62.

Произвести смыкание ряда по имеющимся данным, характеризующим общий объем продукции промышленности в одном из регионов (в фактически действующих ценах), млн руб.

Уровни продукции	2003г.	2004г.	2005г.	2006г.	2007г.	2008г.	2009г.
В старых границах	20,1	20,7	21,0	21,2	-	-	-
В новых границах	-	-	-	23,8	24,6	25,5	27,2

Задача 63.

До 2003 г. в состав производственного объединения входили 20 предприятий. В 2003г. в него влились еще 4 предприятия, и оно стало объединять 24 предприятия. Произвести смыкание ряда динамики двумя способами.

Годы
Реализованная продукция по 20 предпр., млн. руб.	448,7	462,8	465,8	491,6	-	-	-	-	-
Реализованна. продукция по 24 предп., млн. руб.	-	-	-	559,5	578,7	580,5	610,0	612,9	615,5

Задача 64.

Имеются следующие данные о поголовье коров в хозяйствах, тыс.голов:

Годы
На 1 января	37,6	38,1	40,1	42,5	-	-	-	-	-
На 1 июля	-	-	-	44,7	44,8	45,0	45,2	46,0	46,1

Установить причину несопоставимости уровней ряда динамики. Привести уровни ряда к сопоставимому виду.

Задача 65.

На основе данных о производстве стиральных машин фирмой за 15 месяцев 2008-2009гг. произведите сглаживание ряда методом трех- и четырехчленной скользящей средней.

месяцы	Стир. машины, тыс. шт.	3-членные скользящие суммы	3-членные скользящие средние	4-членные скользящие суммы	4-членные скользящие средние (нецентрир.)	4-членные скользящие средние (центрир.)

Задача 66.

Имеются данные о розничном товарообороте во всех каналах реализации в регионе, млрд руб:

Месяцы	2007г.	2008г.	2009г.
Январь	7,4	7,8	8,3
Февраль	7,9	8,2	8,6
Март	8,7	9,2	9,7
Апрель	8,2	8,6	9,1
Май	7,9	8,3	8,8
Июнь	8,2	8,7	9,1
Июль	8,3	8,8	9,3
Август	8,8	9,3	9,9
Сентябрь	8,7	8,9	9,3
Октябрь	8,8	8,2	9,9
Ноябрь	8,3	8,8	9,8
Декабрь	9,0	9,5	9,3

Для изучения общей тенденции розничного товарооборота региона по месяцам за 2007-2009гг. произведите: 1) преобразование исходных данных путем укрупнения периодов времени в квартальные уровни; 2) сглаживание квартальных уровней товарооборота с помощью скользящей средней. Изобразите графически фактические и сглаженные уровни ряда динамики. Сделайте выводы о характере общей тенденции розничного товарооборота во всех каналах реализации в регионе.

Задача 67.

В таблице приведены данные о динамике производства молока в регионе за 2006-2010гг.:

Годы						Итого
Производства молока в регионе, млн. т	13,3	13,5	14,8	16,1	16,6	74,3

Проверьте ряд динамики на автокорреляцию. Произведите аналитическое выравнивание ряда динамики по прямой. Сделайте выводы о характере общей тенденции изучаемого явления, изобразите графически полученные данные. С помощью полученного уравнения тренда сделайте точечный и интервальный прогноз. Оцените колеблемость уровней ряда динамики от тренда.

Задача 68.

Имеются следующие данные о среднем размере товарных запасов в универмаге по месяцам года, млн. руб.:

21,2	21,3	21,2	21,3	21,2	21,0	21,0	20,2	19,2	20,1	20,8	21,1

Проведите: 1) сглаживание ряда товарных запасов универмага методом 4-членной скользящей средней; 2) выравнивание ряда динамики по прямой. Сделайте выводы о характере общей тенденции изучаемого явления.

Задача 69.

В таблице приведены данные об урожайности зерновых в одном из регионов:

Годы
Урожайность, ц/га	17,0	14,4	19,7	23,0	22,1	23,8

1) Проверьте ряд динамики на автокорреляцию.

2) Произведите аналитическое выравнивание ряда динамики по прямой.

3) Сделайте точечный и интервальный прогноз на 2001 год.

4) С помощью критерия Дурбина-Ватсона проверьте остаточные величины на автокорреляцию.

5) Оцените колеблемость уровней ряда динамики от тренда.

Задача 70.

Имеются следующие данные о розничном товарообороте одного из предприятий региона (млн.руб.):

месяц
у	7,4	7,5	7,8	8,0	8,7	9,8	10,7	11,3	12,2	13,0	14,0	15,5

По данному ряду динамики требуется выполнить следующее:

1) Проверьте ряд динамики на автокорреляцию;

2) выполнить сглаживание ряда методом 3-х членной скользящей средней;

3) провести аналитическое выравнивание ряда динамики по параболе второго порядка;

4) проверьте остаточные величины на автокорреляцию.

Задача 71.

Определите индексы сезонности методом постоянной средней по данным из таблицы:

Численность рабочих фирмы по месяцам, чел.

Месяцы	Численность на 1 число месяца
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь

Задача 72.

Определите индексы сезонности методом постоянной средней по данным из таблицы:

Внутригодовая динамика числа расторгнутых браков

населения города по месяцам за 1995-1997 гг.

Месяцы	Число расторгнутых браков	Индекс сезонности %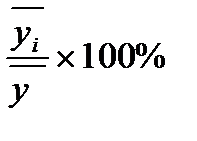
			В среднем за 3 года ( )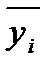
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Средний уровень ряда ( )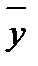

Задача 73.

Имеются следующие данные в регионе о числе родившихся и числе зарегистрированных браков по месяцам 1996-1997гг.:

Месяцы	Число родившихся	Число зарегистрированных браков
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Всего

Для анализа внутригородской динамики числа родившихся и числа зарегистрированных браков определить индексы сезонности: а) методом постоянной средней; б) методом аналитического выравнивания по прямой. Представьте графически сезонную волну развития изучаемых явлений по месяцам года.

Задача 74.

Имеются данные о производстве цемента в 2 странах, млн