Лекция 1.1. матрицы и определители
ЛЕКЦИЯ 1.1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Впервые понятие матрица появилось в середине 19-го века в работах У.Гамильтона, А. Кели и Дж. Сильвестра. Основы теории матриц созданы К.Вейерштрассом и Г.Фробениусом во второй половине 19 - го – начале 20 - го вв. Современное обозначение матрицы (две вертикальные черты) ввел А.Кели в 1848 г.
"Матричный" язык, обозначения и матричные вычисления широко используются в современной математике и её приложениях.
Основные области применения матричной алгебры:
- математика (решение систем линейных уравнений, линейное программирование, теория собственных значений, теория вероятностей …);
- теоретическая электротехника (исследование малых колебаний электрических систем…);
- физика (механика, математическая физика, квантовая механика …).
Понятие матрицы
Определение. Совокупность 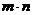 выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей размера
выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей размера 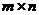 .
.
Обозначение матрицы А размера 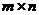 :
:
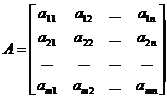 (1)
(1)
Выражения 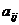 , из которых составлена матрица, называются элементами матрицы, первый индекс i соответствует номеру строки, второй индекс j – номеру столбца, на пересечении которых стоит элемент.
, из которых составлена матрица, называются элементами матрицы, первый индекс i соответствует номеру строки, второй индекс j – номеру столбца, на пересечении которых стоит элемент.
Элементами матрицы могут быть: числа (в этом случае говорят о числовых матрицах) и другие математические объекты (векторы, многочлены, дифференциалы и даже матрицы)
Другие обозначения матрицы:
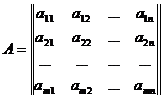 .
.
Также используются краткие обозначения: ( 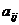 ), [
), [ 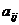 ] или ||
] или || 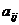 ||.
||.
Иногда матрицы обозначают просто заглавными латинскими буквами A = ( 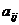 ). Когда хотят указать размер матрицы, пишут
). Когда хотят указать размер матрицы, пишут 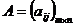 или
или 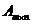 .
.
Примеры матриц:
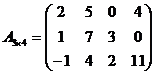 ;
; 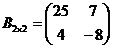 ;
; 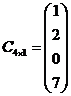 ;
; 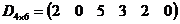 .
.
Частные виды матриц
Если m = n, т.е. число строк равно числу столбцов, то матрица называется квадратной матрицей порядка n.
Вид квадратной матрицы:
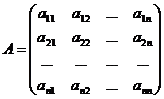 (2)
(2)
Квадратная матрица называется
верхней треугольной матрицей, если 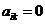 для всех i > k;
для всех i > k;
нижней треугольной матрицей, если 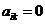 для всех i < k.
для всех i < k.
Матрица размером 1хn, состоящая из одной строки, называется матрицей-строкой (вектор-строкой)
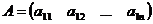 или A = (
или A = (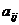 )1xn. (3)
)1xn. (3)
Матрица размером mx1, состоящая из одного столбца, называется матрицей-столбцом (вектор-столбцом)
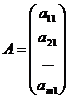 или A = (
или A = (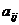 )mx1 (4)
)mx1 (4)
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 0 или (0)mxn (в алгебре матриц эта матрица играет роль нуля).
Квадратная матрица, в которой отличны от нуля только элементы, стоящие на главной диагонали, называется диагональной ( 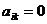 для всех
для всех 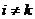 ).
).
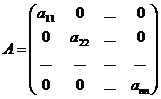 (5)
(5)
Диагональная матрица, в которой все элементы главной диагонали – единицы, называется единичной матрицей и обозначается символом E (в алгебре матриц эта матрица играет роль единицы).
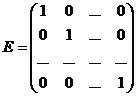 или
или 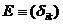 , где
, где 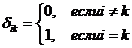 . (6)
. (6)
ОПРЕДЕЛИТЕЛИ
Понятие определителя
Понятие "определитель" впервые было введено Г.Лейбницем при решении систем линейных уравнений (1693г.). В 1750 г. метод определителей был вновь разработан Г.Крамером, затем дополнен А.Вандермондом (1772г.). Термин "определитель" в современном его значении ввел О.Коши (1815 г.), а обозначения – вертикальные линии – А.Кели.
Приложения определителей:
- математика (векторная алгебра, аналитическая геометрия, линейная алгебра…)
- электротехника (расчет электрических цепей…)
- физика.
Каждой квадратной матрице А порядка n можно однозначно поставить в соответствие число, которое называется определителем (детерминантом) матрицы А и обозначается:
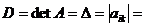
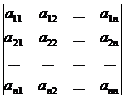 (1)
(1)
По определению определитель n-го порядка матрицы А равен алгебраической сумме n! произведений, в каждое из которых входит только по одному элементу из каждой строки и каждого столбца матрицы А.
Вычисление определителей
Определители 2-го порядка
Определение. Определителем второго порядка называется число,вычисляемое по формуле:
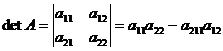 . (2)
. (2)
Мнемоническое правило для вычисления определителей 2-го порядка: определитель равен произведению главных диагональных элементов минус произведение побочных диагональных элементов.
Приведенное правило можно проиллюстрировать рисунком:



– +
Пример 1.
1. Вычислить определитель: 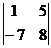 .
.
Решение:
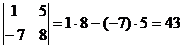
2. Решить уравнение: 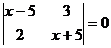
Решение:
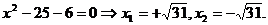
Определители 3-го порядка
Определение. Определителем третьего порядка называется число, вычисляемое по формуле:
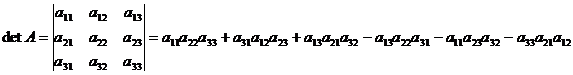 (3)
(3)
Мнемонические правила для вычисления определителей 3-го порядка:
Правило треугольников




+ –
Правило Саррюса
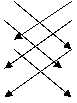

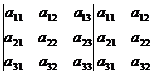
 –
– 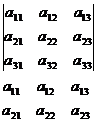 +
+
– – – + + +
Пример 2.Вычислить определитель третьего порядка 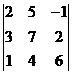 .
.
Решение.
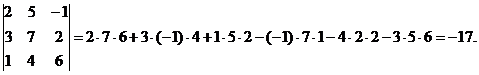
Свойства определителей
Определитель не изменится, если поменять в нем местами строки и столбцы, т.е. транспонировать определитель.
Например: 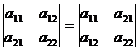 .
.
Для доказательства достаточно вычислить левые и правые части и сравнить их.
Замечание. Из свойства 1 следует равноправность строк и столбцов определителя. Поэтому все свойства, сформулированные для строк определителя, верны и для столбцов, и наоборот.
Перестановкадвух строк или двух столбцов определителя меняет лишь знак определителя.
Например.
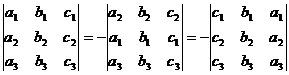 .
.
Свойство доказывается аналогично предыдущему.
Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю.
Доказательство: из условия равенства строк (столбцов) и свойству 2 следует D = – D, т.е. 2D = 0, или D = 0.
Например. 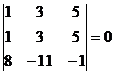 .
.
Умножение всех элементов одного столбца или одной стоки определителя на одно и то же число k равносильно умножению определителя на это число, или: общий для всех элементов строки или столбца множитель можно выносить за знак определителя.
Например:
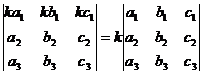 .
.
Если все элементы какого-либо столбца или строки равны нулю, то и сам определитель равен нулю.
Это свойство следует из предыдущего при k = 0.
Если элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
Доказательство: Пусть 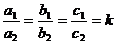 или
или 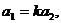
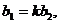
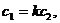 и
и 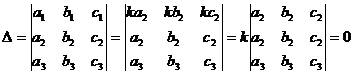 .
.
Обобщим свойства 3, 5 и 6:
Определитель равен нулю тогда и только тогда, когда:
a) Две строки или два столбца определителя равны друг другу;
b) Одна строка или один столбец определителя состоят из нулей;
c) Две строки или два столбца определителя пропорциональны друг другу.
При сложении двух определителей, различающихся только одной строкой (или столбцом), соответствующие элементы этой строки (столбца) складываются, т.е. справедливо следующее равенство:
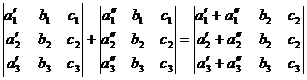 .
.
Равенство проверяется вычислением левой и правой частей.
Определитель не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно т то же число. Или: прибавление кратного к-ой строки к i-ой строке не изменяет значения определителя (i¹k).
Например:
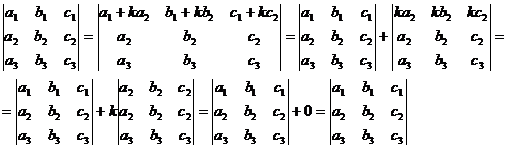 .
.
Пользуясь свойствами определителей, можно избежать лишних вычислений.
Например:
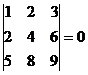 , по свойству 6, так как элементы 1-ой и 2-ой строки пропорциональны.
, по свойству 6, так как элементы 1-ой и 2-ой строки пропорциональны.
Обратная матрица
Понятие обратной матрицы используют при решении систем линейных уравнений.
Определение. Обратной матрицей по отношению к квадратной матрице А порядка n называется матрица А-1 порядка n, удовлетворяющая равенству:
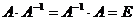 (1)
(1)
Вычисление обратной матрицы.
Если detA ¹ 0, то обратную матрицу можно вычислить по формуле:
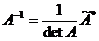 , (2)
, (2)
где
- detA – определитель матрицы А;
- 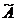 – присоединенная матрица;
– присоединенная матрица;
- * – знак операции транспонирования.
Определение. Присоединенной матрицей называется матрица, составленная из алгебраических дополнений элементов аij, т.е. матрица вида:
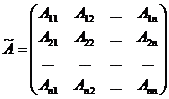 , (3)
, (3)
где Аij–алгебраические дополнения элементов аij матрицы А.
Порядок вычисления обратной матрицы:
- Вычислить определитель матрицы detA;
- Составить присоединенную матрицу 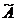 ;
;
- Транспонировать матрицу 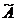 (получить матрицу
(получить матрицу 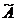 *);
*);
- Записать обратную матрицу по формуле 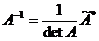 .
.
Пример 1. Вычислить обратную матрицу для матрицы 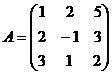 .
.
Решение:
1. Вычислим определитель матрицы:
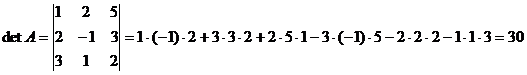 .
.
2. Составим присоединенную матрицу:
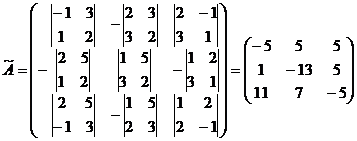 .
.
3. Транспонируем матрицу 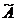 :
:
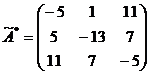 .
.
4. Вычислим А-1:
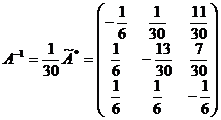 .
.
Замечание. Из правила вычисления обратной матрицы следует условие её существования: обратная матрица существует, если определитель матрицы не равен нулю (матрица невырожденная).
Определение. Квадратная матрица, определитель которой равен нулю, называется вырожденной матрицей, вырожденная матрица называется также особенной.
Ранг матрицы
Вычисление ранга матрицы
Перечислим основные способы вычисления ранга матрицы:
1. Простой перебор определителей.
2. Метод окаймляющих миноров.
3. Метод элементарных преобразований – приведение с помощью элементарных преобразований матрицы А к трапециевидной матрице А¢ того же ранга.
Метод окаймляющих миноров
Пусть в матрице найден минор к-го порядка М, отличный от нуля. Рассмотрим лишь те миноры (к+1)-го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен к. В противном случае среди окаймляющих миноров найдется ненулевой минор (к+1)-го порядка, и вся процедура повторяется.
Пример 3.Найти ранг матрицы 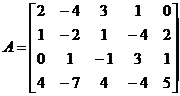 .
.
Решение.
Фиксируем минор 2-го порядка, отличный от нуля:
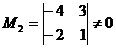 .
.
Минор 3-го порядка, окаймляющий минор М2, также отличен от нуля:
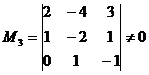 .
.
Однако, оба минора 4-го порядка, окаймляющие М3, равны нулю:
М4 = 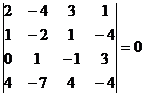 , М4 =
, М4 = 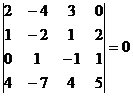 .
.
Поэтому ранг матрицы равен трем (r = 3).
Ответ: r = 3
Метод элементарных преобразований
Метод элементарных преобразованийоснован на том факте, что элементарные преобразования не меняют её ранга. Используя эти преобразования, любую матрицу можно привести к трапециевидному виду, или к такому виду, когда все её элементы, кроме главных диагональных элементов 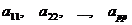 , равны нулю.
, равны нулю.
Удобно, когда главные диагональные элементы трапециевидной матрицы равны единице, т.е. трапециевидная матрица имеет вид:
 .
.
Тогда ранг матрицы равен числу главных диагональных элементов (в данном случае – единиц), отличных от нуля.
Пример 4. Найти ранг матрицы 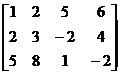 .
.
Решение.
Приведем исходную матрицу к трапециевидной форме.
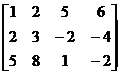 ®
® 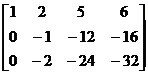 ®
® 
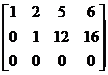 ®
® 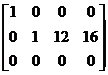 ®
® 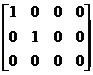 .
.
Число единиц, стоящих на главной диагонали полученной трапециевидной матрицы равно двум, следовательно, ранг этой матрицы равен двум, таков же и ранг исходной матрицы, т.е. r = 2.
Ответ: r = 2.
Литература по теме:
а) основная
1. Кремер Н.Ш. Высшая математика для экономического бакалавриата: учебник и практикум. М.: Юрайт, 2014. – 909 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/EDF405ED-E895-42DE-9744-ED48C83187DC#/).
б) дополнительная
2. Красс М.С. Математика в экономике. Базовый курс. М.: Юрайт, 2015. – 471 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/8BD2AC05-D7E3-4B22-844C-3DC3D6F52A1B#/).
ЛЕКЦИЯ 1.1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Впервые понятие матрица появилось в середине 19-го века в работах У.Гамильтона, А. Кели и Дж. Сильвестра. Основы теории матриц созданы К.Вейерштрассом и Г.Фробениусом во второй половине 19 - го – начале 20 - го вв. Современное обозначение матрицы (две вертикальные черты) ввел А.Кели в 1848 г.
"Матричный" язык, обозначения и матричные вычисления широко используются в современной математике и её приложениях.
Основные области применения матричной алгебры:
- математика (решение систем линейных уравнений, линейное программирование, теория собственных значений, теория вероятностей …);
- теоретическая электротехника (исследование малых колебаний электрических систем…);
- физика (механика, математическая физика, квантовая механика …).
Понятие матрицы
Определение. Совокупность 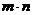 выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей размера
выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей размера 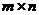 .
.
Обозначение матрицы А размера 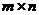 :
:
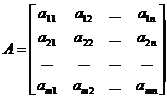 (1)
(1)
Выражения 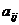 , из которых составлена матрица, называются элементами матрицы, первый индекс i соответствует номеру строки, второй индекс j – номеру столбца, на пересечении которых стоит элемент.
, из которых составлена матрица, называются элементами матрицы, первый индекс i соответствует номеру строки, второй индекс j – номеру столбца, на пересечении которых стоит элемент.
Элементами матрицы могут быть: числа (в этом случае говорят о числовых матрицах) и другие математические объекты (векторы, многочлены, дифференциалы и даже матрицы)
Другие обозначения матрицы:
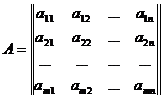 .
.
Также используются краткие обозначения: ( 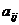 ), [
), [ 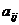 ] или ||
] или || 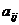 ||.
||.
Иногда матрицы обозначают просто заглавными латинскими буквами A = ( 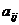 ). Когда хотят указать размер матрицы, пишут
). Когда хотят указать размер матрицы, пишут 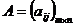 или
или 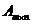 .
.
Примеры матриц:
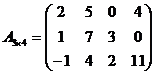 ;
; 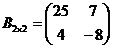 ;
; 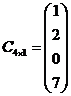 ;
; 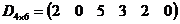 .
.
Частные виды матриц
Если m = n, т.е. число строк равно числу столбцов, то матрица называется квадратной матрицей порядка n.
Вид квадратной матрицы:
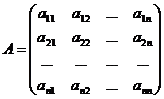 (2)
(2)
Квадратная матрица называется
верхней треугольной матрицей, если 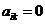 для всех i > k;
для всех i > k;
нижней треугольной матрицей, если 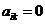 для всех i < k.
для всех i < k.
Матрица размером 1хn, состоящая из одной строки, называется матрицей-строкой (вектор-строкой)
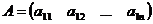 или A = (
или A = (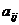 )1xn. (3)
)1xn. (3)
Матрица размером mx1, состоящая из одного столбца, называется матрицей-столбцом (вектор-столбцом)
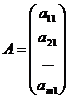 или A = (
или A = (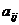 )mx1 (4)
)mx1 (4)
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 0 или (0)mxn (в алгебре матриц эта матрица играет роль нуля).
Квадратная матрица, в которой отличны от нуля только элементы, стоящие на главной диагонали, называется диагональной ( 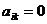 для всех
для всех 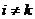 ).
).
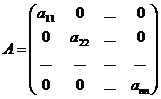 (5)
(5)
Диагональная матрица, в которой все элементы главной диагонали – единицы, называется единичной матрицей и обозначается символом E (в алгебре матриц эта матрица играет роль единицы).
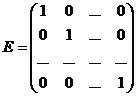 или
или 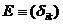 , где
, где 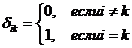 . (6)
. (6)
