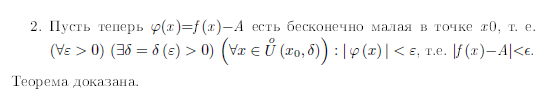Переход к пределу в неравенстве, устойчивость знака

Определение пределов

Данное определение дано по Коши.

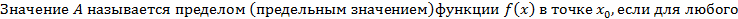
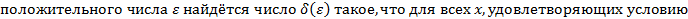
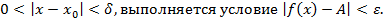
Единственность предела

Теорема: предел функции единственен.

Доказательство: Пускай, 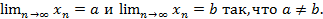Тогда, возьмём некую окрестность 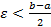. В таком случае, по свойству предела последовательности, все числовые значения предела последовательности должны будут сходиться в двух окрестностях сразу, что вызывает противоречие.

Переход к пределу в неравенстве, устойчивость знака

Теорема: если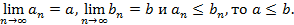

Доказательство: от противного, если a>b. Возьмём число rтакое, что a>r>b.

Тогда, с одной стороны, найдётся такое N’, что для n>N’ будет a_n<r. С другой же найдётся и такой номер N’’, что для n>N’’ будет r<b_n. В таком случае, a_n>b_n, что противоречит условию.

Теорема: если f(x) в точке a положительна, то она будет положительна в некоторой окрестности этой точки.

Принцип сжатой переменной

Теорема: если a_n<b_n<c_n, то если a_nи c_nпри стремлении nк бесконечности равны, то b_n также равен им.

5)Бесконечно малые, большие и ограниченные функции\последовательности, основные теоремы

Бесконечно малая – функция\последовательность, которая стремится к нулю.

Бесконечно большая – функция\последовательность, которая стремится к бесконечности определённого знака.

Ограниченная же стремится к какому-то числу.

Основные теоремы:

1. Если f(x) в некой точке бесконечно мала, то 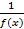в этой точке будет бесконечно велика.

Возьмём в качестве 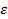такое число, что |f(x)|< 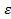, тогда 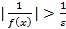. Отсюда следует вывод, что последовательность бесконечно велика.

2.

3.

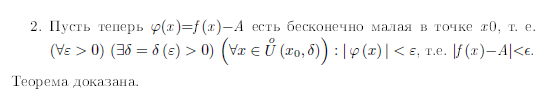
Сравнение бесконечно малых, основные теоремы

Говорят, что a(x) – бесконечно малая более высокого порядка малости, чем b(x), если 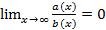, (в случае, если поменять местами, будет бесконечность).

Говорят, что они имеют одинаковый порядок малости, если данный предел будет равняться вещественному числу.

Говорят, что их порядок малости одинаковый, если данный предел будет равен 1.

1.

2.

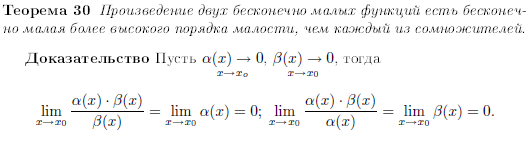
3.

Основные теоремы о пределах

1. О пределах в равенстве, если g(x)=f(x), то их пределы равны.

2. О пределах в неравенстве, было доказано ранее.

3. Предел постоянной равен постоянной.

4. Единственность предела, было доказано ранее.

5.

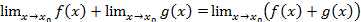
Доказательство: Пускай, пределы f(x)=aи g(x)=b – бесконечно малые.

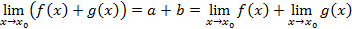
6. Аналогично с произведением.

7. Аналогично с частным.

Существование предела однородной последовательности

Материал не найден

Критерий Коши существования предела

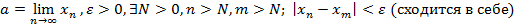
Замечательные пределы

Первый замечательный предел: .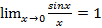

Второй замечательный предел: .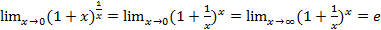

Непрерывность функции в точке, определение и теоремы

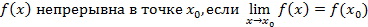
Вариант по Коши:

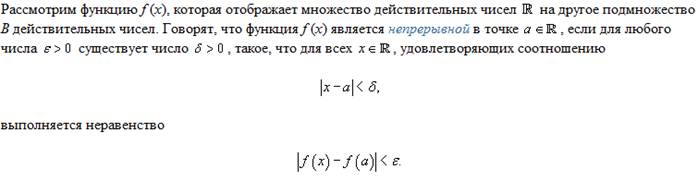
Теоремы:

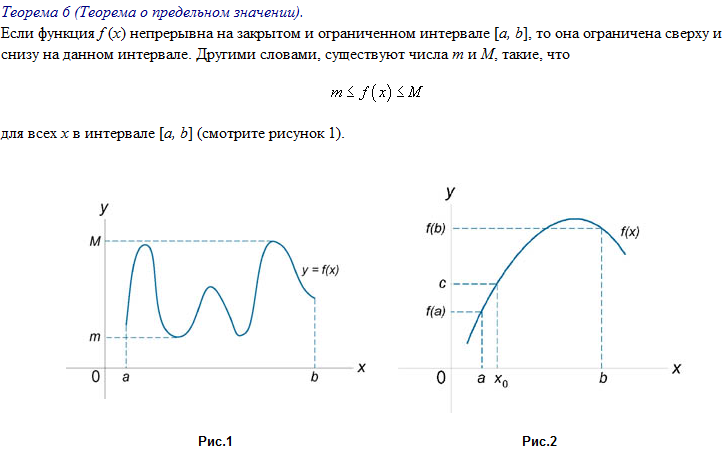
Односторонний предел, односторонняя непрерывность

В формуле предела по Коши:

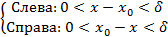
Предел, который стремится своему значению только с одной стороны.

В таком случае, для конечных пределов справа\слева есть конечная непрерывность справа\слева.

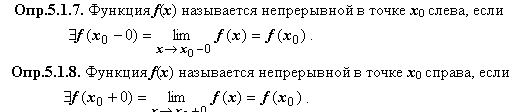
Классификация разрывов

Первого порядка: предел справа и предел слева конечны. Функция визуально имеет «угол».

Второго порядка: если хотя бы один предел стремится кплюс\минус бесконечности или не существует. Функция визуально «разорвана».

Таблица производных, правила дифференцирования

17)Дифференциал, дифференцируемость функции, инвариантность первого дифференциала

Дифференциалом называется произведение f’(x)dx, или dy.

Дифференциал – линейная часть приращения функции.

Теоремы Ферма и Ролля

Ролля

Для прямолинейной функции это доказывается просто. Докажем для непрямолинейной.

Ферма

Частный случай. Теорема гласит, что на приведённом выше промежутке есть максимум или минимум. Собственно говоря, если производная равна нулю, то это одно из двух, без доказательства.

Теоремы Лагранжа и Коши

Лагранж

Коши

Чисто в принципе, это – частный случай Лагранжа. По крайней мере, доказывается так же.

Вместе (b-a) и (x-a) в дополнительной функции мы записываем вторую функцию от этих аргументов, доказывая, что обе дроби в формуле Коши равны нулю.

Формулы Тейлора и Маклорена

Формула Тейлора имеет вид:

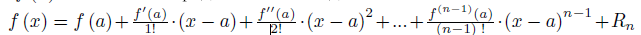
Формула Маклорена – её частный случай, в ней a=0.

Любую f(x) можно разложить по данной формуле.

R_n – остаточный член, его формула (по Лагранжу): .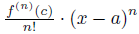

Sinx

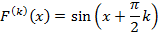
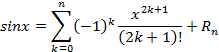
Cosx

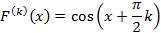
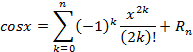
4)ln(1+x)

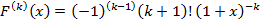
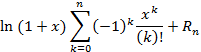
5(1+x)^M

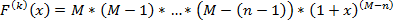
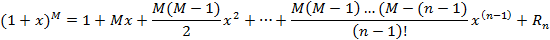
Без производной

· Область определения\значения

· Специфика (чет\нечет)

· Разрывы, асимптоты

· Ключевые точки (x\y=0)

Первая производная

· Область определения\значения для первой производной

· Точки экстремума

· Поведение функции (растёт\убывает)

Вторая производная

· Область определения\значения для второй производной

· Точки перегиба

· Выпуклость\вогнутость

Определение пределов

Данное определение дано по Коши.

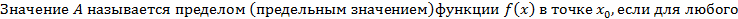
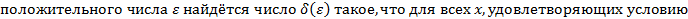
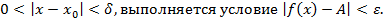
Единственность предела

Теорема: предел функции единственен.

Доказательство: Пускай, 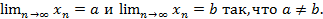Тогда, возьмём некую окрестность 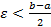. В таком случае, по свойству предела последовательности, все числовые значения предела последовательности должны будут сходиться в двух окрестностях сразу, что вызывает противоречие.

Переход к пределу в неравенстве, устойчивость знака

Теорема: если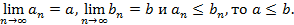

Доказательство: от противного, если a>b. Возьмём число rтакое, что a>r>b.

Тогда, с одной стороны, найдётся такое N’, что для n>N’ будет a_n<r. С другой же найдётся и такой номер N’’, что для n>N’’ будет r<b_n. В таком случае, a_n>b_n, что противоречит условию.

Теорема: если f(x) в точке a положительна, то она будет положительна в некоторой окрестности этой точки.

Принцип сжатой переменной

Теорема: если a_n<b_n<c_n, то если a_nи c_nпри стремлении nк бесконечности равны, то b_n также равен им.

5)Бесконечно малые, большие и ограниченные функции\последовательности, основные теоремы

Бесконечно малая – функция\последовательность, которая стремится к нулю.

Бесконечно большая – функция\последовательность, которая стремится к бесконечности определённого знака.

Ограниченная же стремится к какому-то числу.

Основные теоремы:

1. Если f(x) в некой точке бесконечно мала, то 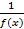в этой точке будет бесконечно велика.

Возьмём в качестве 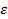такое число, что |f(x)|< 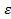, тогда 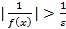. Отсюда следует вывод, что последовательность бесконечно велика.

2.

3.