Плоскость, плоскость в трёхмерном пространстве

Способы задать плоскость:

· Три точки.

· Точка и нормаль.

· Две прямые.

Формы записи плоскости:

· В отрезках на осях:

Где a,b,c – координаты пересечения осей плоскостью.

· Векторная запись:

(r-r₀)·N=0

Где rи r₀ – радиус вектора некоторых принадлежащих плоскости точек, а N–нормаль вектор.

· Проходящей через некую точку:

A(x-x₀)+B(y-y₀)+C(z-z₀)+D=0

Где (A,B,C) – координаты нормаль вектора.

· Общее:

Ax₀+By₀+Cz₀+D=0

Где (A,B,C) – координаты нормаль вектора.

Угол между двумя плоскостями можно найти по следующей формуле:

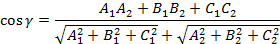
Условие параллельности двух плоскостей:

Где A,B,C – координаты нормалей.

Условие перпендикулярности двух плоскостей:

Данные условия необходимы и достаточны.

Прямая, прямая в трёхмерном пространстве

Способы задать прямую:

· Через точку и ненулевой вектор.

· Через две точки.

Формы записи прямой:

· Векторная

r=r₀+lS

Где rи r₀-радиус векторы принадлежащих прямой точек, S–направляющий вектор.

· Параметрическая

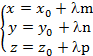
Где (m,n,p) – координаты направляющего вектора, 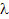-параметр, нулевые xyz–координаты некой точки, принадлежащей прямой.

· Каноническая

Где (m,n,p) – координаты направляющего вектора, нулевые xyz–координаты некой точки, принадлежащей прямой.

· Через две точки

Где первые и вторые xyz–координаты принадлежащих прямой точек.

Угол между двумя прямыми можно найти по следующей формуле:

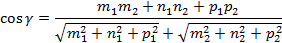
Где mnp– координаты направляющих векторов.

Условие параллельности двух прямых:

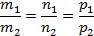
Где mnp– координаты направляющих векторов.

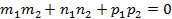
Где mnp– координаты направляющих векторов.

Данные условия необходимы и достаточны.

Плоскость и прямаяв трёхмерном пространстве

Относительно плоскости прямая может:

· Пересекать плоскость

· Быть ей параллельной

· Быть ей перпендикулярной

· Принадлежать ей

Углом между прямой и плоскостью называется угол между прямой и её проекцией на плоскость.

Формула угла между прямой и плоскостью:

Где (A,B,C) – координаты нормали плоскости, (m,n,p) – направляющий вектор прямой.

Необходимое и достаточное условие параллельности прямой и плоскости:

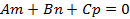
Необходимое и достаточное условие перпендикулярности прямой плоскости:

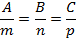
Прямая на плоскости

Формы записи прямой:

· Каноническая

· Общая

Ax+By+C=0

· С угловым коэффициентом

Формула угла для двух прямых на плоскости:

Кривые второго порядка

Общее уравнение кривой второго порядка:

Где хотя бы один из параметров A,B,C не равен нулю.

Эллипс

Частный случай эллипса - круг.

Такая замкнутая кривая, что сумма расстояний от любой её точки до двух фокусов одинакова и равна 2а.

Формула эллипса (каноническая):

Где b²=a²-c², а и b– большая и малая полуоси, c–полурасстояние между фокусами.

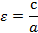
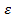Где – эксцентриситет (0< <1).

Уравнение касательной:

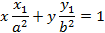
Гипербола

Такая кривая, что модуль разности расстояний от любой её точки до двух фокусов является величиной постоянной и равно 2а.

Формула гиперболы (каноническая):

Где b²=a²-c², а и b– реальная и мнимая полуоси, c–полурасстояние между фокусами.

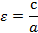
Где – эксцентриситет ( >1).]

Асимптоты гиперболы:

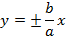
Уравнение касательной:

Парабола

Множество точек на плоскости, равноудалённых от прямой (директрисы) и точки (фокусы).
Каноническое уравнение:

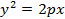
Где p – параметр параболы.

Уравнение касательной:

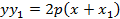
Поверхности второго порядка

Общее уравнение кривой второго порядка:

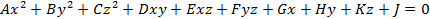
Где хотя бы один из параметров A,B,C,D,E,F не равен нулю.

Эллипсоид

Частный случай эллипсоида – сфера (все три оси одинаковы).

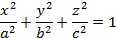
Однополостный гиперболоид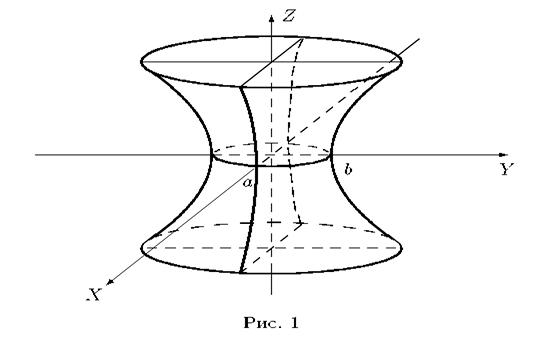

Двуполостный гиперболоид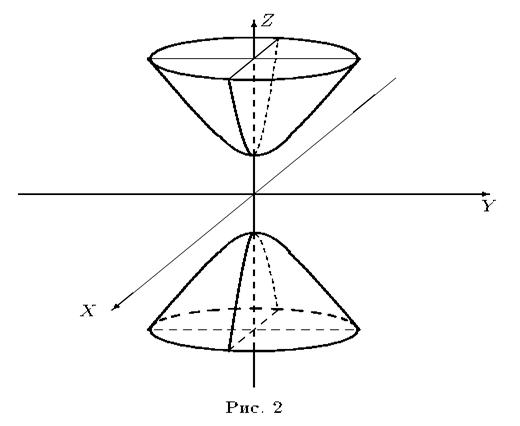

Эллиптический параболоид

Гиперболический параболоид

Цилиндр

Конус

13,14)Линейное пространство. Определение, примеры. Базис. Размерность. Разложение вектора по базису

Линейное пространство – математическая структура, которая формируется векторами.

В любом линейном пространстве есть 2 операции:

1. Сложение. Для любой суммы векторов есть существующий в пространстве результат.

2. Умножение на скаляр. Для любого умноженного на скаляр вектора есть существующий в пространстве результат.

На операции накладываются следующие условия:

1. 1·x=x

2. x+y=y+x

3.

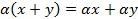
4.

5.

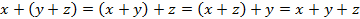
6.

7.

8.

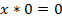
В каждом пространстве существует некоторая размерность – максимально возможный набор линейно независимых векторов. Любой другой вектор можно получить набором этих векторов, причём только одним.

Базис же является совокупностью этих векторов.

Примером линейных пространств можно привести двухмерное и трёхмерное Декартовы xyz.