Построение типовой матрицы рисков

Типовая матрица рисков (см. рисунок 4.1) включает следующие основные элементы: поле ячеек с заголовком (например, «Уровни рисков»), поле шкалы частот, включающее заголовок («Уровни частоты») и качественные характеристики интервалов частот, поле шкалы последствий, включающее заголовок («Уровни тяжести последствия») и качественные характеристики интервалов последствий.

Матрица рисков строится на основе заданной размерности поля ячеек m x n, согласующего коэффициента μ, соотношения сторон ячейки a/b и рассчитанных в соответствии с п. 6.3 значений уровней шкал частот и последствий. При этом обеспечивается шкала рисков, у которой граница между областями значений нежелательного и недопустимого риска соответствует заданному уровню R_доп.

При построении матрицы рисков в первую очередь формируется поле ячеек, затем добавляются остальные элементы.

6.4.1 Построение поля ячеек

Поле ячеек строится следующим образом.

1) На основе ячейки с заданным соотношением сторон формируется структура, содержащая m x n ячеек (на рисунке 6.3 в качестве примера приведено поле ячеек 6 x 4 с ячейкой, у которой a/b =0,5).

2) По формуле (3) вычисляется |tgθ| (в нашем примере для a/b =0,5 он будет равен (–1)).

3) С заданным тангенсом угла наклона проводится отрезок прямой, проходящей через центр симметрии поля ячеек (см. рисунок 6.3, где она показана черной штриховой линией).

4) Вычисляется горизонтальный шаг g между граничными прямыми (на основе формулы (5)):

.

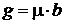Предположим, что в нашем примере μ = 1,5, тогда g будет в 1,5 раза больше ширины b ячейки.

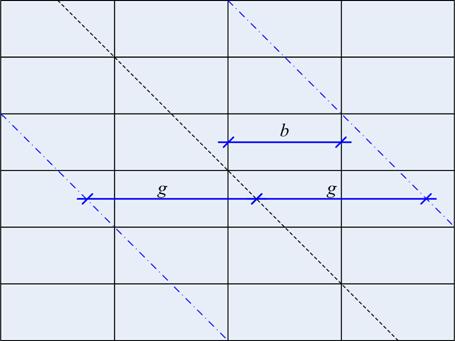
Рисунок 6.3 – Разделение поля ячеек на области значений риска

5) Со смещением на шаг g влево и вправо от наклонного отрезка прямой проводится еще 2 отрезка с таким же наклоном (на рисунке 6.3, они показаны штрих-пунктирными линиями). Таким образом, на поле ячеек образуется 4 сегмента (области значений риска), разделяемых тремя наклонными отрезками. Причем, отрезок в правой верхней части поля является частью прямой R = R_доп.

6) Для полученной конфигурации поля ячеек выполняется присвоение ячейкам категории риска путем установления цвета ячейки в соответствии с цветовым кодом. При этом принадлежность к области значений риска определяется тем, где находится большая часть площади ячейки. В результате получается поле, показанное на рисунке 6.4.

7) На следующем этапе на поле ячеек наносятся точки риска.

Поскольку система координат матрицы рисков имеет логарифмический масштаб, то для определения положения центра точки риска на поле ячеек следует определить ее линейные координаты в данной системе. Пусть задана точка риска, у которой частота равна f₁ и удельный размер последствий равен c₁. Будем считать координатой центра точки риска по частоте смещение h₁ от левого нижнего угла поля ячеек по вертикали, а по последствиям – смещение w₁ от левого нижнего угла поля ячеек по горизонтали:

, .

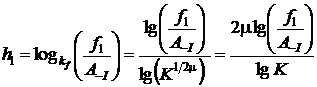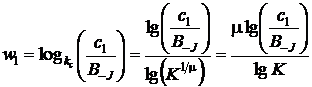Рисунок 6.4 – Вид поля ячеек после присвоения ячейкам категории риска

Данные смещения выражены в количестве единиц высоты a и ширины b ячейки, что является не удобным для практического применения. Преобразуем последние выражения для расчета координат точки в миллиметрах:

, ,

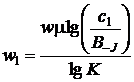(22)

где h – высота ячейки, мм, w – ширина ячейки, мм.

6.4.2 Объединение поля ячеек и остальных элементов матрицы рисков

Поскольку задачей настоящих МР является построение матрицы рисков с применением количественных оценок, то в структуру матрицы рисков добавляются необходимые элементы.

Для формирования матрицы рисков к полю ячеек, включающему точки риска, присоединяются следующие элементы матрицы рисков (см. Приложение А):

- поле наименования и интервалов шкалы частот;

- поле меток шкалы частот;

- поле наименования и интервалов шкалы последствий;

- поле меток шкалы последствий;

- поле наименования матрицы рисков;

- поле дополнительных сведений.

При этом на поле ячеек не отображаются вспомогательные линии, использовавшиеся для разделения системы координат на области значений риска и присвоения ячейкам категории риска.

В результате получается матрица рисков, пример которой приведен на рисунке 6.5.

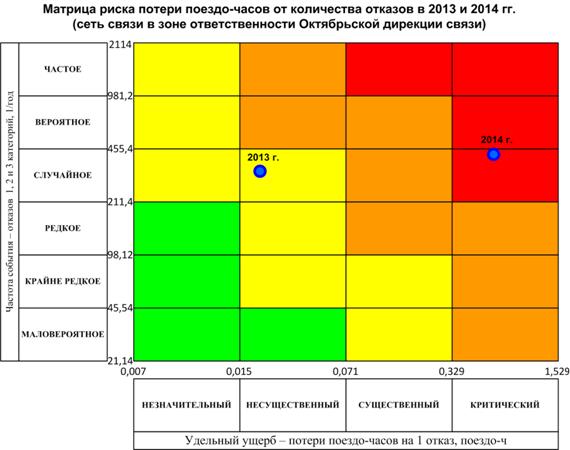
Рисунок 6.5 – Пример матрицы рисков

6.4.3 Рекомендации по подготовке исходных данных

В качестве примера в таблице 6.1 приведены статистические данные по нежелательному событию вида «отказ услуги сети железнодорожной электросвязи», которое имеет в качестве последствий потери поездо-часов из-за задержки движения поездов.

Таблица 6.1 – Данные по отказам услуг сети железнодорожной электросвязи

Год наблюдения
Количество отказов 1, 2 и 3 категории
Суммарные потери CΣ, поездо-часов	91,27	122,3	92,47	33,78	53,57		212,9
Частота отказов технических средств, f, 1/год
Удельные потери, c, поездо-часов (на 1 отказ)	0,089	0,119	0,136	0,081	0,154	0,218	0,727

1) На основании статистических данных о количестве нежелательных событий данного вида за интервал наблюдения вычисляется частота их возникновения:

,

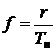(23)

где r – количество нежелательных событий данного вида за интервал наблюдения; T_н – интервал наблюдения (год, час).

Рекомендуемое значение интервала наблюдения Т_н составляет 1 год.

Рассчитанные значения заносятся в строку 3 таблицы 6.1.

2) По статистическим данным размеров последствий от возникновения нежелательных событий данного вида за заданный интервал наблюдения определяется удельный размер последствий (средний размер последствий на одно нежелательное событие):

,

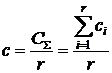(24)

где С_Σ – суммарный размер последствий от нежелательного события за интервал наблюдения;

с_i – размер последствий от i-го (i = 1…r) нежелательного события, ед.;

r > 0 – количество нежелательных событий данного вида за интервал наблюдения.

Рассчитанные значения заносятся в строку 4 таблицы 6.1.

3) Выбираем минимумы и максимумы частот и удельных размеров последствий из выборки за расширенный интервал наблюдения (5 и более лет). Если такого большого объема выборки не имеется, то используем все доступные данные.

В таблице 6.1 минимальное и максимальное значения частоты составляют 293 и 1031 1/год соответственно; минимальное и максимальное значения удельного размера последствий составляют 0,081 и 0,727 поездо‑час соответственно.

Далее на основе данных значений, а также заданного допустимого уровня риска R_доп выполняется расчет параметров шкал частот, последствий и рисков (п. 6.3).

6.4.4 Рекомендации по выбору размерности матрицы и согласующего коэффициента

Основным ограничением, накладываемым на матрицу рисков, которая строится согласно настоящим МР, является область значений коэффициента K масштаба шкалы рисков. Так, при K > 26 оценка риска становится грубой, поскольку в пределах одной категории рисков их уровни могут значительно отличаться. Ограничение K также ограничивает диапазон значений шкал частот и последствий.

Если требуется больший диапазон шкал, то он может быть расширен путем увеличения размерности матрицы. Так, например, при увеличении размерности матрицы рисков с 6 x 4 до 8 x 6 диапазон значений шкалы частот возрастает в K^1/m раз, а последствий – в K^2/m раз (то есть, например, если K = 10, m = 1,5, то диапазон значений шкалы частот возрастает в 4,64 раза, а последствий – в 21,5 раз).

Также возможен случай, когда уровни рисков, соответствующие отображаемым на матрице точкам риска, имеют значительный разброс. В этом случае одним из решений проблемы является увеличение размерности матрицы, иногда в сочетании с выбором более низкого значения m. Например, если перейти от матрицы 6 x 4 с m = 1,5 к матрице 6 x 4 с m = 1, то при K = 10 диапазон значений шкалы частот возрастает в 316 раз, а последствий – в 3162 раза.

В большинстве случаев рекомендуется применение матрицы риска размерностью 6 x 4 с m = 1,5. При недостаточности ее диапазонов значений могут использоваться предложенные выше способы.

Пример расчета параметров и построения матрицы рисков представлен в Приложении Г.

Рекомендации по расширению функциональности типовой матрицы рисков

6.5.1 Рекомендации по отображению точек риска, выходящих за пределы поля ячеек матрицы риска.

Одной из проблем матрицы рисков является ситуация, когда точка риска не попадает в границы поля ячеек матрицы рисков. Выше был рассмотрен вариант решения данной проблемы путем увеличения диапазонов шкал частот, последствий и рисков. Но данный вариант требует перестроения матрицы рисков, включая пересчет значений шкал частот и последствий. Поэтому представляет интерес задача введения в матрицу рисков дополнительных элементов, позволяющих в компактном виде, пусть даже с потерей точности, отображать любые сочетания частоты и удельного размера последствий, лежащие за пределами шкал матрицы рисков.

Для выполнения указанных требований рекомендуется расширенная матрица рисков, где для отображения рисков, лежащих вне диапазонов шкал, применяются дополнительные элементы.

Поставленная задача заключается в том, чтобы ввести в матрицу рисков дополнительные области, позволяющие качественно (с указанием категории риска) отобразить значения частоты и/или удельного размера последствий, выходящие за пределы диапазона шкал частот (F_min…F_max) и (C_min…C_max)последствий матрицы рисков (Рисунок 6.6).

Рисунок 6.6 – Области значений рисков, лежащих за пределами поля ячеек матрицы рисков

На рисунке 6.6 вся область системы координат, не охваченная полем ячеек матрицы рисков, поделена на 8 сегментов:

- O1 – F < F_min, C_min £C £ C_max;

- O2 – F > F_max, C_min £C £ C_max;

- O3 – C < C_min, F_min £F £ F_max;

- O4 – C > C_max, F_min £F £ F_max;

- O5 – F < F_min, C < C_min;

- O6 – F > F_max, C < C_min;

- O7 – F < F_min, C > C_max;

- O8 – F > F_max, C > C_max.

Очевидно, что возможные категории риска для каждого из сегментов O1…O8 зависят от конкретной конфигурации матрицы. Рассмотрим конфигурацию размерностью 6 x 4 с m = 1,5 (рисунок 6.7).

Рисунок 6.7 – Возможные категории риска для каждого из сегментов O1…O8 (матрица размерностью 6 x 4 с m = 1,5)

Из рисунка 6.7 очевидно, что сегмент O1 пересекают прямые R = R_доп/K и R = R_доп/K². Из этого следует, что в сегменте O1 будут присутствовать категории риска, где R £ R = R_доп/K² (риск, не принимаемый в расчет), R_доп/K² < R £ R_доп/K (допустимый риск) и R_доп/K < R £ R_доп (нежелательный риск). Поскольку прямая R = R_доп не пересекает данный сегмент, то недопустимые риски в нем присутствовать не будут.

Аналогично рассуждая для других сегментов, получим следующие возможные категории:

- O1 – риск, не принимаемый в расчет, допустимый риск, нежелательный риск;

- O2 – допустимый риск, нежелательный риск, недопустимый риск;

- O3 – риск, не принимаемый в расчет, допустимый риск;

- O4 – нежелательный риск, недопустимый риск;

- O5 – риск, не принимаемый в расчет;

- O6, O7 – риск, не принимаемый в расчет, допустимый риск, нежелательный риск, недопустимый риск;

- O8 – недопустимый риск.

Исходя из полученных результатов, в типовую матрицу рисков вводятся дополнительные элементы, позволяющие отобразить точки риска, выходящие за пределы поля ячеек – области (их границы на рисунке обозначены розовыми прямоугольниками), которые разделяются по углам поля ячеек матрицы штриховыми линиями. Также штриховые линии проведены от левой и нижней границ поля ячеек к меткам шкал частот и последствий. Таким образом, точка риска, попадающая за пределы области поля ячеек, может быть отображена в дополнительных полях. При этом она заключается в квадрат, закрашиваемый по цветовому коду соответствующей категории риска (см. рисунок 6.8).

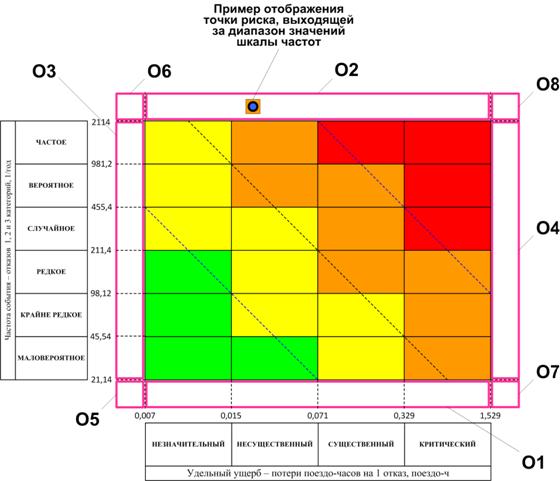
Рисунок 6.8 – Расположение дополнительных элементов в матрице рисков

Представленная модификация матрицы рисков позволяет также отображать риски, где частота либо удельный размер последствий равны 0 (в области O5).

Форма расширенной матрицы рисков приведена в Приложении Б.

6.5.2 Рекомендации по повышению точности принадлежности точки риска к категории риска

Как было показано выше (п. 5.4), классический подход к построению матрицы рисков на основе ячеек имеет конечную погрешность; при этом трудно обеспечить погрешность лучше 10%.

При оценке риска могут возникнуть случаи, когда погрешность оценивания риска на уровне 10% является недопустимой. Тогда возникает задача модификации матрицы рисков для реализации погрешности, близкой к нулю.

Поскольку наиболее точной из графических форм представления результатов оценки риска является график риска, можно преобразовать поле ячеек в область системы координат, нарушив при этом принятые выше правила присвоения ячейкам категорий риска. Если допустить, что ячейка является условным элементом и может отображать риски не одной, а двух категорий, то в случае применения такой матрицы рисков любая точка риска будет (в соответствии с цветовым кодом) принадлежать той области значений, в которой находится ее количественный уровень риска. Таким образом, погрешность оценивания риска будет минимальной.

Форма поля ячеек матрицы рисков высокой точности приведена в Приложении В.

Рекомендации по интегральной оценке риска

При комплексном управлении рисками возникает задача получения интегральной оценки для нескольких рисков различных видов. При этом данные риски могут представляться в различных единицах последствий (например, рубли, количество травм, потери поездо-часов и т. п.). Главной проблемой при интегральной оценке нескольких рисков является отсутствие единой единицы их измерения. Самым приемлемым вариантом является введение эквивалентных оценок рисков, исчисляемых в денежном выражении. Эквивалентные оценки являются необходимыми с точки зрения анализа затрат и выгод, поскольку, в конечном счете, главным результатом управления рисками является минимизация экономических потерь.

Другой проблемой является наличие у риска каждого вида собственного допустимого уровня и собственных шкал рисков, частот и последствий, каждая их которых имеет специфический диапазон значений и масштаб. В связи с этим представление интегральной оценки рисков в виде матрицы рисков не представляется возможным. Практически единственным вариантом является представление результатов интегральной оценки рисков на одномерной шкале (такой же, как на рисунке 5.1б) с введением унифицированного масштаба, как правило, с применением полуколичественных единиц (баллов).

Если эквивалентные оценки рисков заданы (то есть, из других единиц измерения уровень риска может быть переведен в потери в денежном выражении), то интегральная оценка рисков возможна по двум критериям, позволяющим для различных вариантов применения получить наиболее объективную оценку:

- качественный критерий, учитывающий соотношение каждого из интегрируемых рисков с установленным для данного риска допустимым уровнем и представляющий положение точки риска на унифицированной одномерной шкале риска; при этом полуколичественные балльные оценки интегрируемых рисков объединяются с равными весами;

- количественный критерий, учитывающий реальные экономические потери от риска данного вида, при этом полуколичественные балльные оценки интегрируемых рисков приобретают вес в зависимости от соотношения величины абсолютных потерь составляющих рисков.

На практике возможно сочетание перечисленных критериев, позволяющее частично учесть абсолютные потери от рассматриваемых рисков.

Интегральная оценка рисков выполняется следующим образом.

Пусть существует n оценок рисков, результаты которых представлены на n матрицах рисков. Таким образом, для каждого i-го из рассматриваемых рисков задан допустимый уровень R_допi, известен масштаб K_i шкалы рисков и для заданного интервала наблюдения известен фактический уровень риска R_i, а также известна его эквивалентная оценка (в денежном эквиваленте).

Для получения интегральной оценки зададим одномерную унифицированную балльную шкалу рисков с логарифмическим масштабом (рисунок 6.9).

Рисунок 6.9 – Одномерная унифицированная балльная шкала рисков

Размерность этой шкалы составляет 40 баллов, по 10 баллов на каждую категорию рисков. При разделении одной области значений рисков на 10 балльных интервалов в логарифмическом масштабе получим относительный шаг 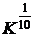;например, при K = 25 один балл будет соответствовать относительному коэффициенту 1,38, что обеспечит приемлемую практическую точность при агрегации нескольких рисков для их интегральной оценки.

В данной шкале для рисков, имеющих уровень ниже принимается минимальная оценка 0 баллов, для рисков, имеющих уровень выше R_доп×K принимается максимальная оценка 40 баллов. Для рисков, уровень которых находится между указанными значениями, количество баллов определяется по формуле:

.

(25)

Интегральная оценка n рисков различных видов заключается в получении некоторого балла B_S, который отражает общую оценку всех составляющих рисков:

,

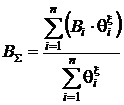(26)

где n – количество интегрируемых рисков;

B_i – балльная оценка i-го риска с уровнем R_i, выполненная по (25);

q_i – весовой коэффициент i-го риска, учитывающий абсолютные потери в денежном выражении;

x = 0…1 – показатель учета абсолютных потерь в денежном выражении (при x = 0 эти потери не учитываются, обеспечивается равновесовая интеграция балльных оценок; при x = 1 вес i-го риска определяется величиной связанных с ним абсолютных денежных потерь).

Весовой коэффициент определяется на основе данных по оценкам рисков в денежном эквиваленте:

,

(27)

где – эквивалентная оценка i-го фактического риска (с уровнем R_i), полученная путем пересчета уровня риска в его оригинальных единицах в денежный эквивалент (в руб.).

Таким образом, существует два «крайних» варианта: с одной стороны, вес каждого интегрируемого риска может определяться на основе реальных финансовых потерь от данного риска (в рублях), а, с другой стороны, может применяться «равновесная» модель, в которой веса рисков равные и имеют значения только баллы (то есть, в каком месте шкалы риска располагается данная точка риска).

На практике, очевидно, крайние оценки менее объективны. Можно рекомендовать выбирать x в диапазоне от 0,33 до 0,67 в зависимости от решаемой задачи (какие именно риски интегрируются и что в их оценке является главным: денежные потери или же соотношение каждого из рисков с соответствующим допустимым уровнем).

Пример интегральной оценки уровня риска приведен в Приложении Д.