Анализ статистических данных

MS EXCEL предоставляет широкие возможности для анализа статистических данных. Для решения простых задач можно использовать встроенные функции. Рассмотрим некоторые из них.

1. Вычисление среднего арифметического последовательности чисел:

=СРЗНАЧ(числа).

Например: =СРЗНАЧ(5;7;9) , =СРЗНАЧ(А1 :А10;С1 :С10), =СРЗНАЧ(А1:Е20).

2. Нахождение максимального (минимального)значения: =МАКС(числа)=МИН(числа). Например: =МАКС(А4:С10);=МИН(А2;С4;7)

3.Вычисление медианы (числа являющегося серединой множества): =МОДА(числа).

Следующие функции предназначены для анализа выборок генеральной совокупности данных.

5.Дисперсия: ДИСП(числа).

6 Стандартное отклонение: =СТАНДОТКЛОН(числа).

7. Ввод случайного числа: =СЛЧИС().

Инструменты пакета анализа

Для решения сложных задач применяется ПАКЕТ АНАЛИЗА.

ПАКЕТ АНАЛИЗА –дополнение EXCEL расширяющее аналитические возможности и позволяющее строить гистограммы, составлять таблицы ранг и персентиль, делать случайные или периодические выборки данных и находить их статистические характеристики, генерировать неравномерно распределенные случайные числа, проводить дисперсионный, регрессионный анализ и многое другое.

Чтобы воспользоваться инструментами анализа, выполните следующие действия:

1) Во вкладке Данные выберите группу Анализи кнопкуАнализ данных -рисунок 3.3.

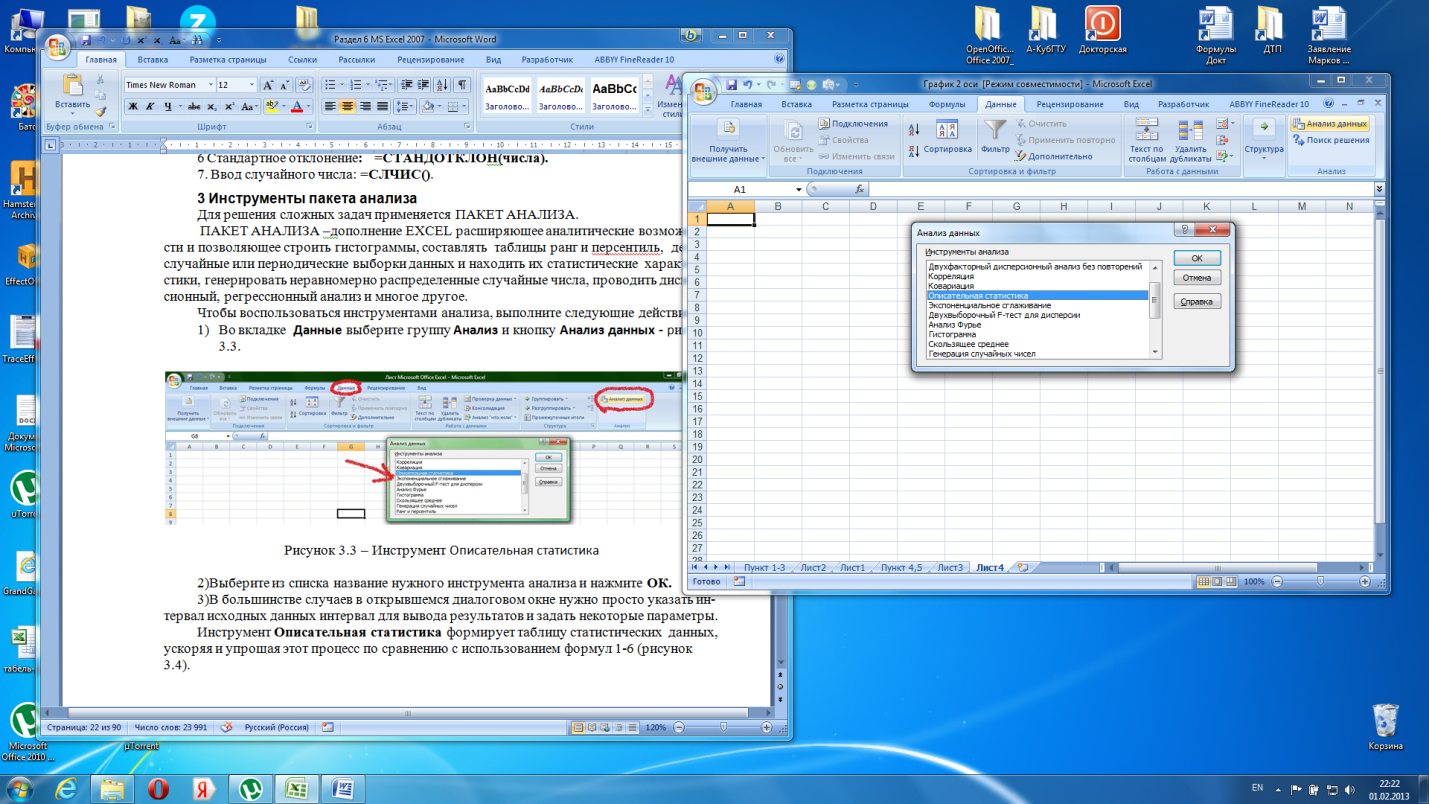
Рисунок 3.3 – Инструмент Описательная статистика

2)Выберите из списка название нужного инструмента анализа и нажмите ОК.

3)В большинстве случаев в открывшемся диалоговом окне нужно просто указать интервал исходных данных интервал для вывода результатов и задать некоторые параметры.

Инструмент Описательная статистика формирует таблицу статистических данных, ускоряя и упрощая этот процесс по сравнению с использованием формул 1-6(рисунок 3.4).

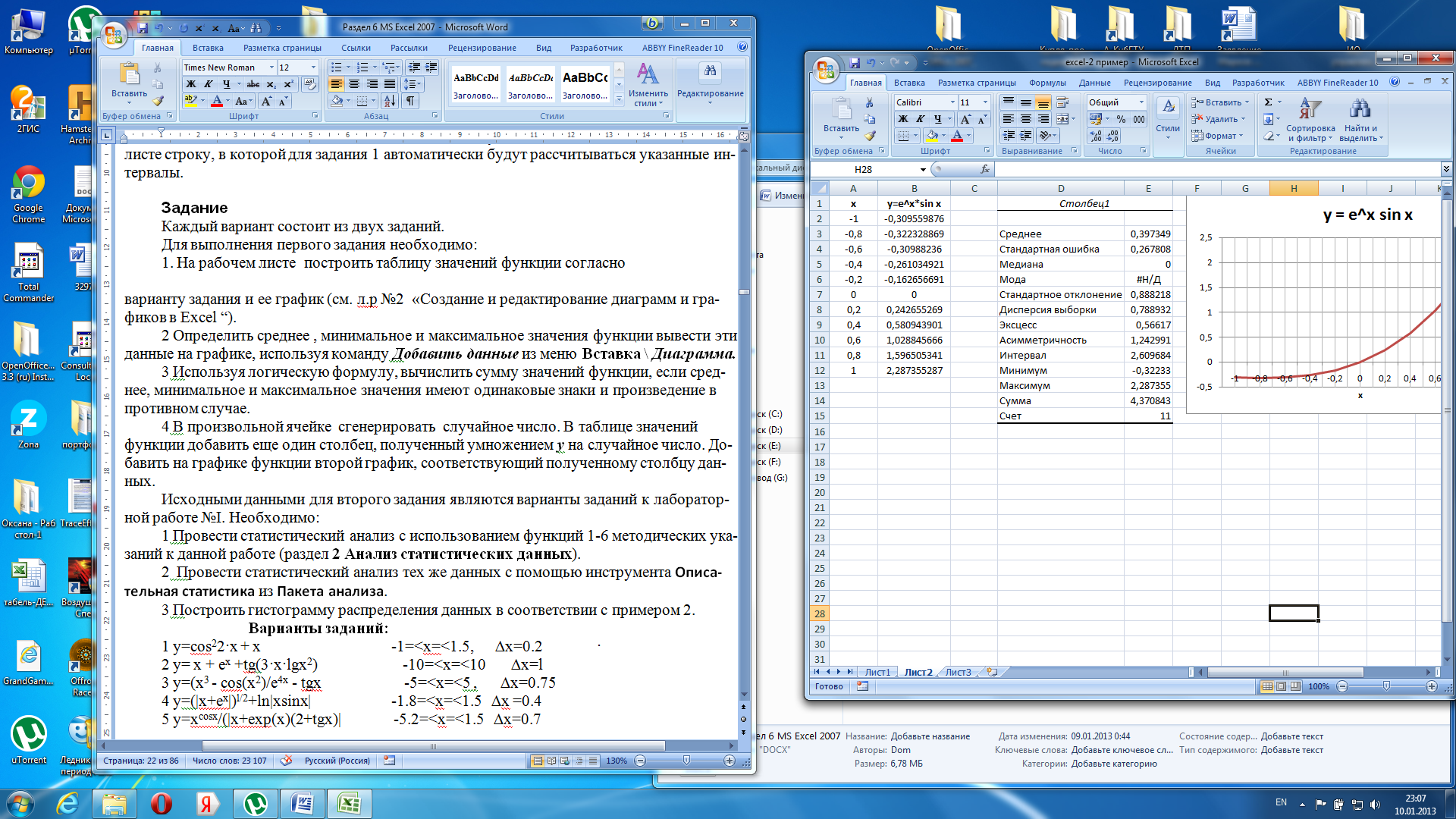
Рисунок 3.4– Обработка столбца В инструментом Описательная статистика

Инструмент Генерация случайных чисел дает возможность получать равномерное и неравномерное распределение.

Инструмент Гистограммапозволяет создавать гистограммы распределения данных.

Область значений измеряемой величины разбивается на несколько интервалов, называемых карманами, в которых в виде столбцов откладывается количество попавших в этот интервал измерений, называемой частотой.

Пример2 Дана таблица с данными о температуре воздуха в Краснодаре летом 2000 года. Интервал измерения от 18°С до 38°С (его можно определить с помощью функций MAKC() и МИН().

1 Разобьем этот интервал на подинтервалы - карманы шириной, например 2°С (ширина карманов не обязательно должна быть равной).

2 Воспользуемся командой Заполнить из меню Главная для быстрого заполнения столбца карманов(значения в столбце будут изменяться от 18 до 38°С с шагом 2°С).

3 Выполним команду Анализ данных из меню Данные, открывшемся диалоговом окне зададим входной интервал (это ячейки с данными о температуре), интервал карманов выходной интервал (надо указать только верхнюю левую ячейку для выхода результатов) и установим флажок Выход графика.

4 После нажатия кнопки ОК на экран будет выведена гистограмма, а рядом со столбцом карманов появится столбец частот, показывающий, сколько дней летом в Краснодаре имели температуру, попадавшую в каждый интервал.

Контрольные вопросы

1 Для чего предназначен ПАКЕТ АНАЛИЗА и каков порядок доступа к его инструментам ?

2 Какие инструменты входят в Пакет анализа?

3 В задании 2 своего варианта вычислите коэффициент вариации.

4 В чем заключаются особенности построения гистограммы распределения данных?

5 Напишите логическую формулу, которая выводит текстовое сообщение «Вычислена сумма» или "Вычислено произведение" в зависимости от того, что было вычислено на рабочем листе в п. 3 задания 1.

Задание

Каждый вариант состоит из двух заданий.

Для выполнения первого задания необходимо:

1. На рабочем листе построить таблицу значений функции согласно варианту задания и ее график (см. л.р №2 «Создание и редактирование диаграмм и графиков в Excel “).

2 Определить среднее , минимальное и максимальное значения функции вывести эти данные на графике, используя команду Добавить данные из меню Вставка \Диаграмма.

3 Используя логическую формулу, вычислить сумму значений функции, если среднее, минимальное и максимальное значения имеют одинаковые знаки и произведение в противном случае.

4 В произвольной ячейке сгенерировать случайное число. В таблице значений функции добавить еще один столбец, полученный умножением у на случайное число. Добавить на графике функции второй график, соответствующий полученному столбцу данных.

Исходными данными для второго задания являются варианты заданий к лабораторной работе №I. Необходимо:

1 Провести статистический анализ с использованием функций 1-6 методических указаний к данной работе (раздел2 Анализ статистических данных).

2Провести статистический анализ тех же данных с помощью инструмента Описательная статистика из Пакета анализа.

3 Построить гистограмму распределения данных в соответствии с примером 2.

Варианты заданий:

1 y=cos²2·x + x -1=<х=<1.5, ∆х=0.2 ·

2 y= x + e^x +tg(3·x·lgx²) -10=<x=<10 ∆x=l

3 y=(x³ - cos(x²)/e^4x - tgx -5=<x=<5 , ∆x=0.75

4 y=(|x+e^x|)^l/2+ln|xsinx| -1.8=<х=<1.5 ∆х =0.4

5 y=x^cosx/(|x+exp(x)(2+tgx)| -5.2=<х=<1.5 ∆х=0.7

6 y=lgx²e^sm2x/lg3x 1=<х=<100 ∆х=5

7 у=е^х+2+1п²(2х)/(х+10е^х) 1=<х==<50 ∆х=2.5

8 y=|sin2x+tg3xl^l/2+e^4x -2.5=<х=<1.5 ∆х=0.4

9 y= l-|sinx|+e^(ln2x+lgx) 1=<х=<10 ∆х=0.1

10 y=(-l)^xe^sinxcosx² 1=<х=<15 ∆х=1

11 y=sin²(2·x) + x -1=<х=<1.5, ∆х=0.2 ·

12 y= sin(x + e^x) +tg(3·x·lgx² ) -10=<x=<10 ∆x=l

13 y=(x³ - 4cos(x²)/e^4x - tgx -5=<x=<5 , ∆x=0.75

14 y=(|x+e^x|)^l/2+lnx^sinx -1.8=<х=<1.5 ∆х =0.4

15 y=x^cosx/(|x+exp(x)(1+tgx)| -5.2=<х=<1.5 ∆х=0.7

16 y=lgx²sm2x/lg3x 1=<х=<100 ∆х=5

17 у=е^х+2+ln²(2х)/(х+10е^х) 1=<х==<50 ∆х=2.5

18 y=|sin2x+tg3x^0,5l/2+e^4x -2.5=<х=<1.5 ∆х=0.4

19 y= l-|sinx|+e^ln2x+lgx 1=<х=<10 ∆х=0.1

20 y=(-l)^xe^sinxcosx² 1=<х=<15 ∆х=1

Содержание отчёта

1Название, цель, содержание работы

2 Задание своего варианта

3 Письменные ответы на контрольные вопросы

4 Выводы по работе

На своём носителе (флэшке) должны быть сохранены результаты работы

Практическое занятие № 4