Навигационная функция высоты светила
Навигационным параметром для определения места по небесным светилам является высота светила h, измеренная над плоскостью истинного горизонта с помощью секстана. Навигационная изолиния - это малый круг на поверхности Земли, принятой за сферу — круг равных высот. С точки зрения геометрии измерение h можно сопоставить с измерением вертикального угла (3 (п. 1.5). Различие заключается в том, что светило находится на бесконечном, с точки зрения практической навигации, расстоянии от Земли, и задачу определения места судна необходимо решать на сфере, а не на плоскости. Получить все аналитические зависимости можно с помощью формул сферической тригонометрии. Существенным здесь является то, что сам радиус сферы в этих формулах никак не задействован, а поэтому для фиксации положения наблюдателя и положения светила можно использовать земную сферу.
Выведем формулу навигационной функции h, для этого обратимся к рис. 1.18, на котором представлено Северное полушарие Земли. В точке 5'(§, /гр) находится
небесное тело (5, /гр - координаты светила, которые являются полной аналогией географических координат). Фактически на некоторой воображаемой сфере, концентрической Земле, называемой Небесной сферой, можно установить соответствие д=(р, /гр=Л. С помощью центрального проектирования светило S(S, trp)
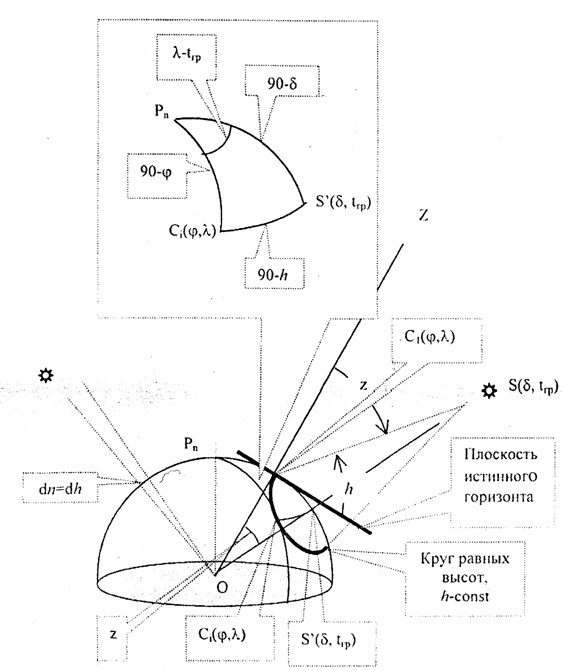
Рис. 1.18. Навигационная функция высоты светила
перенесено на поверхность Земли в точку S'{8, trp). Наблюдатель находится в точке С)((рЛ) или в любой другой точке С,((рЛ), из которых над горизонтом измерен навигационный параметр h. В точке Ci((pA) показана плоскость истинного горизонта (касательная плоскость), проведена нормаль к поверхности, указываююия-ЧйР зенит. Угол z между нормалью и направлением на светило называется w^bwS^M5:
расстоянием. В соответствии с рис. 1.18 h + z = 90, светило видно под от^мй к
горизонту не в одной точке, а на некоторой кривой, все точки которой равноудалены от проекции светила S ', Этот малый круг с полюсом в точке S ' — круг равных высот.
Рассмотрим сферический треугольник Рп S'C,. В этом треугольнике сторона CfS ' = 2 = 90-h, точка С, - проекция зенита Z на земную сферу. Теперь по теореме косинуса стороны сферического треугольника запишем навигационную функцию h:
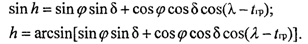
Высота измеряется в плоскости вертикала светила, которая ориентирована по направлению азимута. Плоскость вертикала образует на поверхности модели Земли, т.е. сферы, большой крут, поэтому элементарное приращение высоты dh=dn, а в соответствии с формулой (1.4), g/i=l. На рис. 1.18 вертикал светила совпадает с его меридианом.
Воспользуемся формулой (1.35), в которой для упрощения будем считать, что \=tzp, т.е. наблюдатель находится на меридиане светила.
Тогда

Итак, теперь установлено, что модуль градиента высоты светила g/,=l, a т/,=А=180°, где А - азимут светила (по нашим условиям наблюдатель и светило находятся на одном меридиане).
