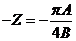Исследование автоколебаний с помощью гармонической линеаризации

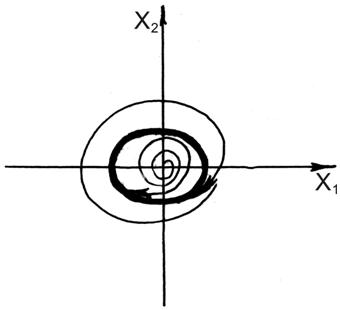
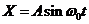Пусть в системе имеют место автоколебания. Будем рассматривать случай . Отыскивать автоколебания будем в виде , т.е.

.

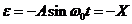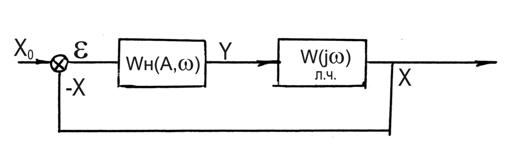
Запишем уравнение данной системы:

,

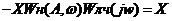откуда — условие автоколебаний.

Или 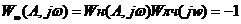(17)

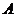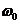Т.е. искомые значения параметров и соответствуют положению системы на границе устойчивости из-за наличия у характеристического уравнения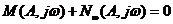

2-х сопряженных мнимых корней.

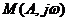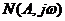Здесь и есть .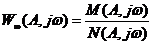

Следовательно, значения 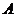и 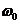могут быть найдены с помощью известных критериев устойчивости линейных систем. При этом 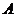и 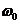варьируют таким образом, чтобы система вышла на границу устойчивости, соответствующую незатухающим колебаниям.

Если пользуемся критерием Гурвица, то добиваемся выполнения равенства 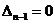, где — предпоследний минор определителя Гурвица, составленного из коэффициентов характеристического уравнения: .

По критерию Михайлова это условие

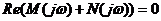
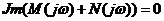
при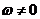

и по критерию Найквиста оно соответствует приведенному выше условию .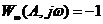

Пример.

; ; ; .

;

;

; ;

.

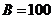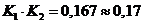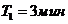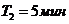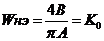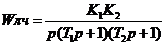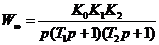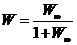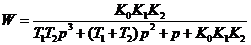Применим критерий Гурвица

,

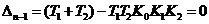отсюда:

;

.

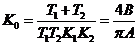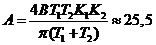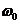определим из условия

;

;

;

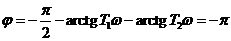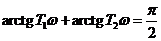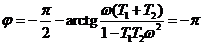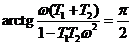, откуда

; .

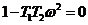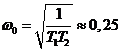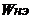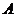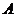Если является нелинейной функцией и , то задача определения и 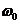значительно усложняется. В этом случае прибегают к методу последовательных приближений или к графическим методам.

С.Л. Гольдфарб предложил графический способ определения 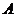и 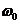, состоящий в следующем:

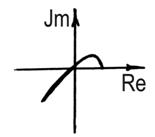
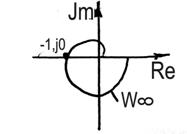
На комплексной плоскости строятся годограф 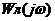, т.е. АФХ линейной части и годограф 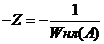— инверсная АФХ нелинейной части. При этом 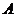указывается как параметр на текущих точках последнего годографа.

В соответствии с (17) точки пересечения годографов определяют искомые значения амплитуды 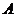и частоты 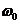автоколебаний.

Имеется ряд правил, позволяющих судить об устойчивости системы:

1) устойчивые автоколебания имеют место, если ветвь обратной АФХ нелинейного элемента от точки пересечения в сторону возрастания 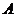лежит вне области, охватываемой АФХ линейной части;

2) САР будет заведомо неустойчивой, если АФХ линейной части ее будет охватывать обратную АФХ нелинейного элемента при возрастании А.

3) если АФХ линейной части системы не охватывает 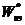, то возникновение автоколебаний (за счет первой гармонической составляющей) невозможно, однако нельзя утверждать на этом основании, что САР будет устойчивой .

Следует заметить, что до определения , мы еще не знали о возможности применения метода гармонической линеаризации.

И только теперь, когда найдена, можно установить, является ли линейная часть фильтром. Т.о., применимость метода гармонической линеаризации приходится определять в конце исследования в порядке проверки.

Метод гармонической линеаризации получил широкое распространение при исследовании нелинейных САР.

Для рассмотренного выше примера применим метод Гольдфарба.

;
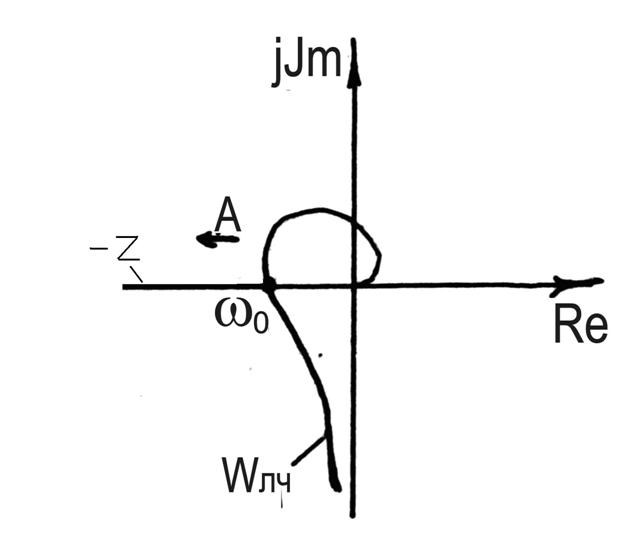
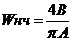