Метод припасовывания (сшивания)
Метод применим при возможности кусочно-линейного представления характеристики нелинейной системы. Он состоит в следующем. Нелинейная характеристика нелинейного звена представляется кусочно-линейной характеристикой.
1. Для каждого линейного участка строим фазовый портрет линейной системы.
2. На фазовой плоскости находим линии переключения с одного линейного участка на другой.
3. Сшиваем фазовый портрет по линиям переключения.
Примеры.
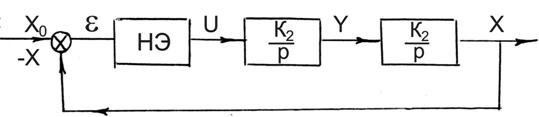
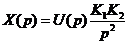 ;
;
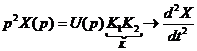 или
или 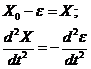 .
.
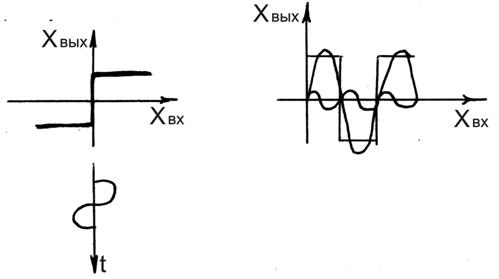
Пусть НЭ имеет характеристику идеального реле.
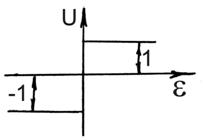
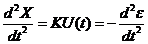 ; если
; если 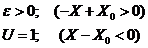
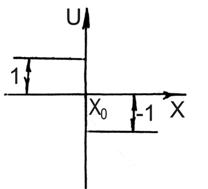
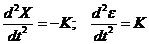 ; если
; если 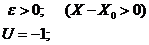 .
.
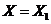 ;
;
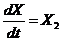 ;
;
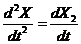 .
.
Для 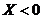 | Для 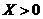 |
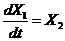 ; ; | 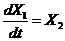 ; ; |
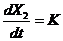 ; ; | 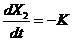 ; ; |
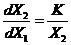 ; ; | 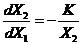 ; ; |
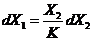 ; ; | 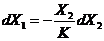 ; ; |
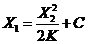 — парабола — парабола | 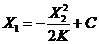 — парабола — парабола |
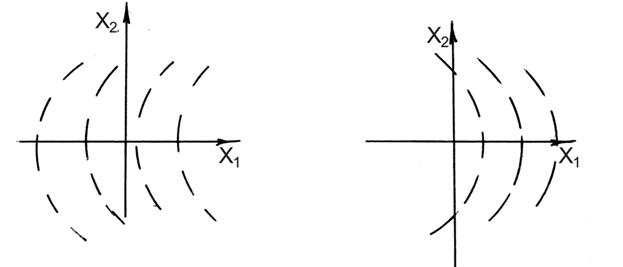
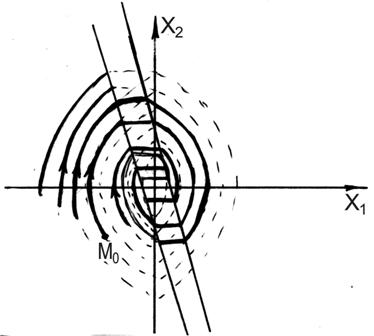
После сшивания.
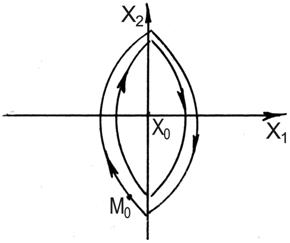
На линии 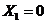 фазовые характеристики сшиваются.
фазовые характеристики сшиваются.
Данный фазовый портрет соответствует колебательному характеру изменения выходной величины.
Теперь заменим идеальное реле звеном: реле с зоной нечувствительности. Тогда получим следующую систему уравнений:
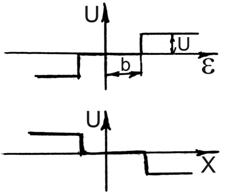
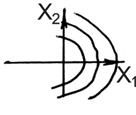 | 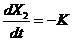 , при , при 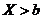 ; ; 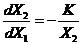 ; ; 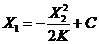 . . |
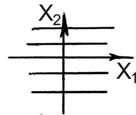 | 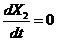 , при , при 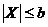 ; ; 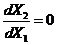 ; ; 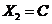 . . |
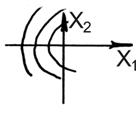 | 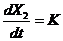 , при , при 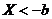 ; ; 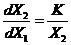 ; ; 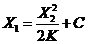 . . |
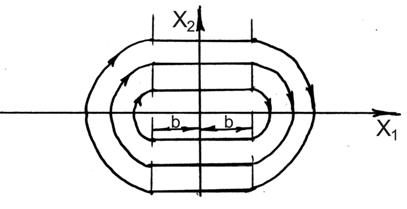
При любых начальных условиях получим незатухающие колебания.
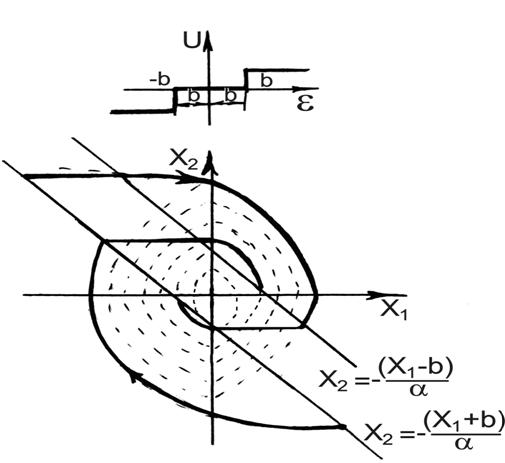
Произведем стабилизацию нелинейной системы.
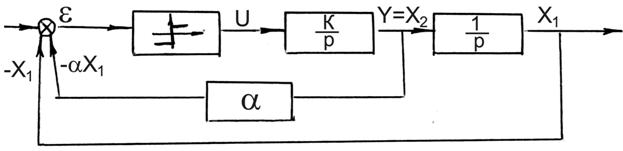
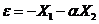
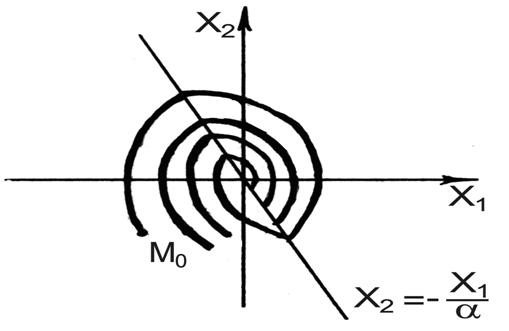
Переключение при
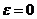
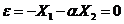 ;
;
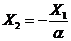 — уравнение линии переключения.
— уравнение линии переключения.
Если нелинейрый элемент имеет характеристику то переключение при:
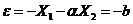 ;
;
т.е. 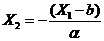 ;
;
и 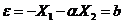 ;
;
т.е. 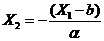 .
.
Метод гармонической линеаризации (гармонического баланса)
Это приближенный метод исследования устойчивости и автоколебаний нелинейных систем. Он дает возможность найти частоту и амплитуду автоколебаний.
Идея метода гармонической линеаризации была предложена в 1934 г. Н.М. Крыловым и Н.Н. Боголюбовым для приближенного определения периодических решений. Применительно к системам автоматического регулирования этот метод развит Л.С. Гольдфарбом и Е.П. Поповым.
Метод применим к системам, содержащим:

Идея метода состоит в замене нелинейной системы такой линейной системой (или близкой к ней), которая в периодических режимах ведет себя как линейная.
Такой подход возможен при выполнении следующих условий.
1). Можно выделить нелинейный и устойчивый линейный элементы.
2). Нелинейный элемент не является частотно преобразующим. Это означает, что если на вход нелинейного элемента поступает гармонический сигнал с частотой 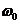 , то и на выходе первая гармоническая составляющая должна быть той же частоты.
, то и на выходе первая гармоническая составляющая должна быть той же частоты.
3). Справедлива гипотеза фильтра.
Будем подавать на вход нелинейного элемента гармонический сигнал:
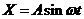 . (1)
. (1)
Предположим, что в нелинейной системе возникают автоколебания.
Покажем, что при некотором условии они близки к гармоническим колебаниям.
При подаче на вход нелинейного элемента сигнала (1) на выходе может быть целый спектр гармоник. Разложив выходной сигнал нелинейного элемента 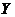 в ряд Фурье, получим:
в ряд Фурье, получим:
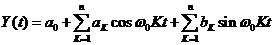 . (2)
. (2)
Если нелинейная характеристика симметрична относительно начала координат, то 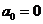 .
.
Теперь сигнал (2) пропустим через линейную часть (ЛЭ).
Пусть его АФХ:
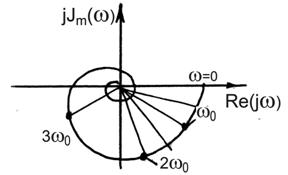
Его составляющие изменяются в зависимости от величины модуля АФХ линейной части для соответствующих частот.
Амплитуду входной составляющей с 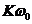 умножаем на модуль
умножаем на модуль 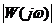 для частоты
для частоты 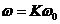 .
.
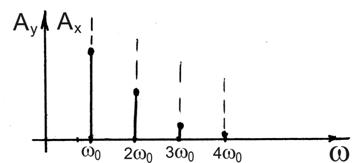
Предположим, что линейная часть является фильтром, совершенно не пропускающим частоты 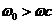 .
.
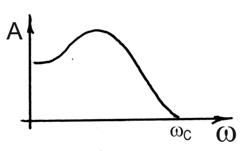
Пусть нелинейная часть порождает гармоники с частотой 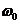 и следующие за первой гармоникой, начиная с частоты
и следующие за первой гармоникой, начиная с частоты 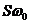 . Тогда независимо от характера нелинейности нелинейного элемента колебания на выходе из линейного звена строго гармонические, если выполняется условие:
. Тогда независимо от характера нелинейности нелинейного элемента колебания на выходе из линейного звена строго гармонические, если выполняется условие: 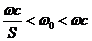 . (3)
. (3)
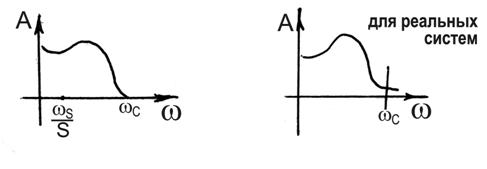
Предположение (3) называется гипотезой фильтра. Оно означает, что линейная часть системы пропускает только первую гармонику выражения (2) с частотой 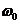 . Т.о., на вход нелинейного элемента снова поступает гармонический сигнал с той же частотой, и вся система ведет себя как линейный объект (циркулирует гармоника одной частоты).
. Т.о., на вход нелинейного элемента снова поступает гармонический сигнал с той же частотой, и вся система ведет себя как линейный объект (циркулирует гармоника одной частоты).
Вместо гипотезы фильтра может быть использована гипотеза резонанса.
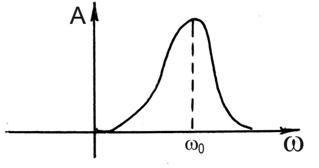
Линейная часть пропускает 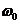 — гармонику с резонансной частотой
— гармонику с резонансной частотой 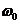 . Однако, для промышленных объектов в подавляющем большинстве справедлива гипотеза фильтра.
. Однако, для промышленных объектов в подавляющем большинстве справедлива гипотеза фильтра.
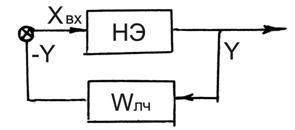
Пусть 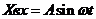 . (1)
. (1)
Нелинейное звено имеет характеристику:
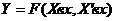 . (2)
. (2)
Разложим выходной сигнал нелинейного элемента в ряд Фурье:
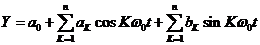 (3)
(3)
где
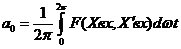 ; (4)
; (4)
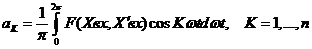 (5)
(5)
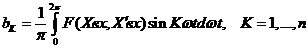 (6)
(6)
Пусть линейная часть пропускает только основную, 1-ую гармонику, постоянной составляющей нет, т.е. 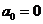 , тогда можно ограничиться:
, тогда можно ограничиться:
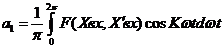 ; (7) при К=1.
; (7) при К=1.
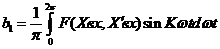 . (8) при К=1.
. (8) при К=1.
Продифференцируем (1)
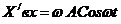 (9)
(9)
Выразим 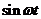 из (1), а
из (1), а 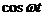 из (9)
из (9)
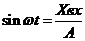 ; (10)
; (10)
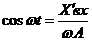 . (11)
. (11)
Теперь (3) запишем в виде:
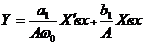 . (12)
. (12)
Преобразуя (12) по Лапласу, получим: 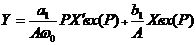 (13)
(13)
откуда
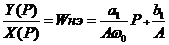 . (14)
. (14)
Обозначая

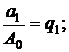
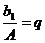
запишем в виде
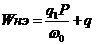 (15)
(15)
Заменяя 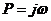 , получим выражение комплексного коэффициента усиления нелинейного элемента:
, получим выражение комплексного коэффициента усиления нелинейного элемента:
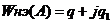 ; (16)
; (16)
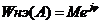 ,
,
где 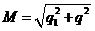 , а
, а 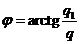 .
.
Коэффициенты 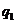 и
и 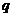 называются коэффициентами гармонической линеаризации.
называются коэффициентами гармонической линеаризации.
Определим коэффициенты 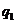 и
и 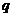 для нелинейности типа:
для нелинейности типа:
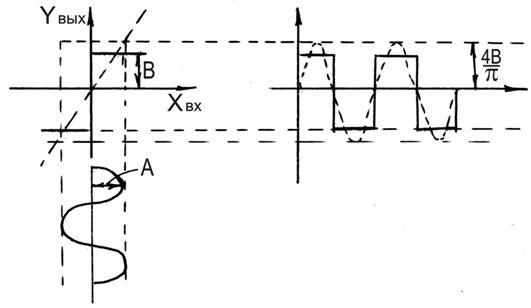
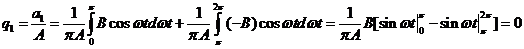
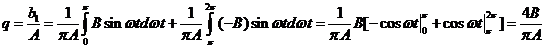
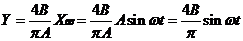 — гармонически линеаризованный сигнал.
— гармонически линеаризованный сигнал.
