Организационно – учебные нормы
61.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
62.
| xi | ||||
| pi | 0,5 | 0,1 | 0,3 | 0,1 |
63.
| xi | ||||
| pi | 0,1 | 0,2 | 0,3 | 0,4 |
64.
| xi | ||||
| pi | 0,6 | 0,1 | 0,1 | 0,2 |
65.
| xi | ||||
| pi | 0,3 | 0,2 | 0,1 | 0,4 |
66.
| xi | ||||
| pi | 0,1 | 0,3 | 0,1 | 0,5 |
67.
| xi | ||||
| pi | 0,1 | 0,2 | 0,4 | 0,3 |
68.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
69.
| xi | ||||
| pi | 0,6 | 0,2 | 0,1 | 0,1 |
70.
| xi | ||||
| pi | 0,3 | 0,2 | 0,4 | 0,1 |
71–80. Известны математическое ожидание a и среднеквадратическое отклонение s нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал (a; b).
71. a = 11, s = 5, a = 5, b = 10.
72. a = 10, s = 4, a = 6, b = 11.
73. a = 9, s = 1, a = 7, b = 12.
74. a = 8, s = 2, a = 4, b = 10.
75. a = 7, s = 3, a = 4, b = 12.
76. a = 6, s = 5, a = 4, b = 8.
77. a = 5, s = 2, a = 2, b = 7.
78. a = 4, s = 3, a = 1, b = 9.
79. a = 3, s = 2, a = 3, b = 8.
80. a = 2, s = 1, a = 1, b = 4.
Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.Методические указания к решению задач
Примеры решения и оформления заданий приведены в учебно-методических пособиях [8] , [9].
Решение системы линейных уравнений по формулам Крамера
Рассмотрим систему уравнений:
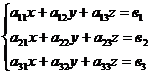 (1)
(1)
где х,у,z – неизвестные; коэффициенты а11, а12,…., а33 и свободные члены 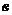 1,
1, 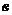 2,
2, 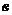 3 – известные постоянные (числа)
3 – известные постоянные (числа)
Введем обозначения:
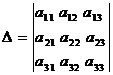 ;
; 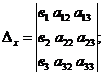
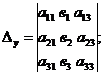
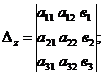
Определитель 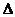 , составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
, составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Определители 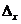 ,
, 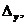
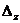 получаются из определителя
получаются из определителя 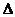 при помощи замены соответственно его первого, второго и третьего столбца – столбцом свободных членов данной системы.
при помощи замены соответственно его первого, второго и третьего столбца – столбцом свободных членов данной системы.
Если 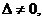 то система (1) имеет единственное решение; оно определяется формулами:
то система (1) имеет единственное решение; оно определяется формулами:
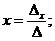
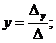
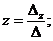 (2)
(2)
Формулы (2) называются формулами Крамера.
Если определитель системы 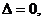 а хотя бы один из определителей
а хотя бы один из определителей 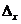 ,
, 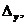
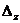 отличен от нуля, то система (1) не имеет решений.
отличен от нуля, то система (1) не имеет решений.
В случае, когда 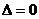 и одновременно
и одновременно 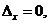
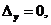
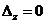 , система (1) также может не иметь решений; но если система в этом случае имеет хотя бы одно решение, то она имеет бесконечно много решений.
, система (1) также может не иметь решений; но если система в этом случае имеет хотя бы одно решение, то она имеет бесконечно много решений.
Задача 2. Используя формулы Крамера, решить систему:
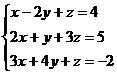
Вычислим сначала главный определитель системы 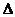 , воспользовавшись следующим правилом вычисления определителей третьего порядка:
, воспользовавшись следующим правилом вычисления определителей третьего порядка:
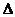 =
= 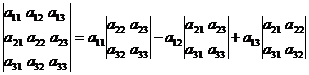 .
.
Имеем
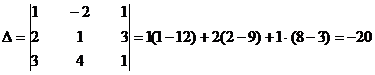
Так как 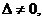 делаем вывод о том, что система имеет единственное решение. Найдём его. Вычислим вспомогательные определители
делаем вывод о том, что система имеет единственное решение. Найдём его. Вычислим вспомогательные определители 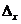 ,
, 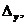
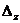 .
.
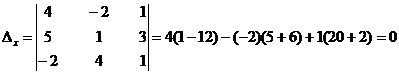 ;
;
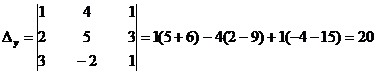 ;
;
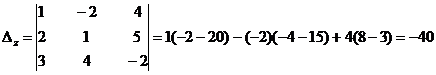 .
.
Далее, воспользовавшись формулами Крамера, окончательно получим
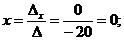
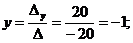
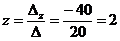 .
.
Осуществим проверку правильности полученного решения, подставив его в каждое уравнение заданной системы:
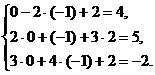
Все три равенства верные, поэтому делаем вывод о правильности полученного решения.
Ответ: х = 0; у = –1; z = 2.
Случайные величины
Случайной величиной называется величина, которая в результате испытания принимает одной возможное числовое значение. Случайные величины (с.в.) обозначаются заглавными латинскими буквами.
Дискретная случайная величина имеет конечное или счетное множество значений. Закон распределения дискретное с.в. Х – это перечень ее возможных значений и соответствующих вероятностей. Закон распределения дискретной с.в. Х записывается в виде ряда распределения:
| Значения (х) | 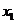 | 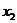 | … | 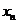 | … | (1) |
| Вероятности (р) | 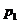 | 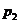 | … | 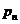 | … |
Здесь 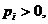
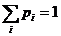 .
.
Непрерывная с.в. принимает любые значения некоторого (возможно, бесконечного) интервала.
Функция распределения с.в. Х – это функция, определенная равенством:
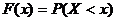 .
.
Свойства функции распределения:
1) 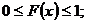
2) 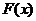 – неубывающая функция;
– неубывающая функция;
3) 
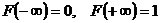 ;
;
4) если все возможные значения случайной величины Х принадлежат интервалу (а,b), то
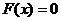 при
при 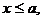
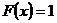 при
при 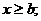
5) 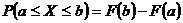 .
.
Числовые характеристики случайной величины.Математическое ожидание дискретной с.в. определяется формулой:
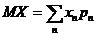
где 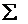 – знак суммирования.
– знак суммирования.
Математическое ожидание обозначается также буквой 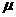 , возможно с индексом, например
, возможно с индексом, например 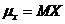 .
.
Перечислим свойства математического ожидания.
- Математическое ожидание константы равно этой константе: МС=С.
- Если С – константа, то М(СХ)=СМХ.
- Математическое ожидание суммы случайных величин равно сумме математических ожиданий.
- Если с.в.
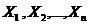 , независимы, то математическое ожидание их произведения равно произведению математических ожиданий.
, независимы, то математическое ожидание их произведения равно произведению математических ожиданий.
Дисперсия дискретной с.в. Х, имеющей закон распределения (1) и математическое ожидание 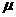 , определяется формулой:
, определяется формулой:
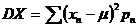 .
.
Дисперсия обозначается также 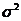 , возможно, с индексом. Можно также доказать, что
, возможно, с индексом. Можно также доказать, что
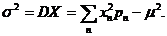
Последняя формула иногда бывает удобней для вычислений.
Перечислим свойства дисперсии.
1. Дисперсия постоянной величины равна нулю.
2. Если С – константа, то 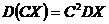 .
.
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
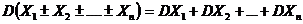 .
.
Средним квадратическим отклонением случайной величины Х называется величина 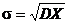 .
.
Задача 7. Дано распределение дискретной случайной величины Х:
| xi | |||||
| pi | 0,1 | 0,2 | 0,1 | 0,3 | 0,3 |
Найти функцию распределения 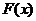 .
.
Решение
Если 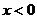 , то
, то 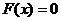 ;
;
если 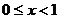 , то
, то 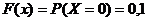 ;
;
если 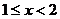 , то
, то 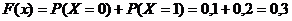 ;
;
если 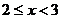 , то
, то 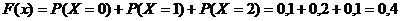 ;
;
если 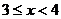 , то
, то 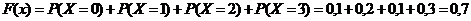 ;
;
если 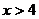 , то
, то 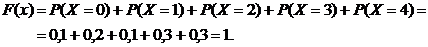
Итак, искомая функция распределения имеет вид:
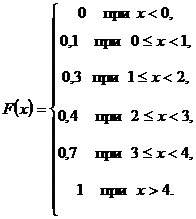
График полученной функции представлен на рис. 1.
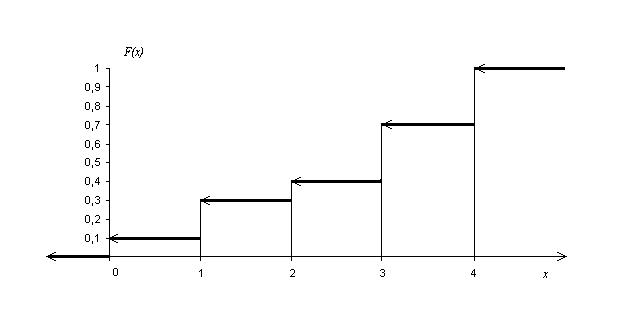
Рис. 1.
Задача 8. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной следующим законом распределения:
| xi | -2 | |||
| pi | 0,5 | 0,1 | 0,2 | 0,2 |
Решение
Вычислим математическое ожидание дискретной случайной величины Х:
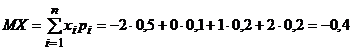 .
.
Далее вычислим дисперсию дискретной случайной величины Х:
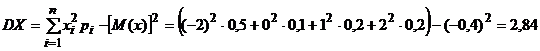 ,
,
а также среднее квадратическое отклонение:
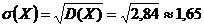 .
.
Ответ: MX = –0,4; DX = 2,84; σX = 1,65.
Нормальное распределение. Еслиплотность распределения непрерывной случайности величины X равна
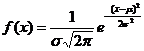 ,
,
то говорят, что с.в. X имеет нормальное распределение; 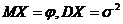 . Если X имеет нормальное распределение с математическим ожиданием µ и средним квадратическим отклонением
. Если X имеет нормальное распределение с математическим ожиданием µ и средним квадратическим отклонением 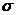 , то вероятности, связанные с X, вычисляются по формулам
, то вероятности, связанные с X, вычисляются по формулам
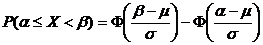 ,
,
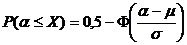 ,
,
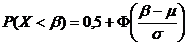 ,
,
где Ф(x) – функция Лапласа; значения функции Лапласа приведены в таблице Приложения 1.
Задача 9. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Написать плотность распределения вероятностей и найти вероятность того, что Х примет значение из интервала (12; 14).
Решение
В нашем случае а = 10, σ = 2, так как случайная величина распределена по нормальному закону, то ее плотность находим следующим образом:
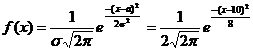 .
.
Вероятность того, что распределенная по нормальному закону случайная величина Х примет значение из интервала (12;14), находится следующим образом:
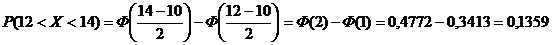 .
.
Ответ: 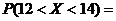
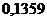 .
.
Приложение 1
Таблица значений функции 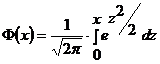
| Сотые доли | ||||||||||
| х | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 | 0,0000 | |||||||||
| 0,5 0,6 0,7 0,8 0,9 | ||||||||||
| 1,0 1,1 1,2 1,3 1,4 | ||||||||||
| 1,5 1,6 1,7 1,8 1,9 | ||||||||||
| 2,0 2,1 2,2 2,3 2,4 | ||||||||||
| 2,5 2,6 2,7 2,8 2,9 | ||||||||||
| 3,0 3,1 3,2 3,3 3,4 | ||||||||||
| 3,5 3,6 3,7 |
Критерии для оценки контрольной работы:
1. Наличие разумных пояснений к выполняемым пунктам задания
2. Указание используемых формул
3. Соблюдение рекомендованного алгоритма решения задания
4. Точность вычислений
5. Решение всех указанных задач.
Перечень вопросов для подготовки к экзамену Часть 1. Линейная алгебра и аналитическая геометрия1. Декартовы координаты на плоскости. Координаты двух точек, симметричных относительно а) оси Ox, б) оси Oy, в) начала координат
2. Расстояние между двумя точками
3. Деление отрезка в данном отношении. Координаты середины отрезка
4. Определение линии на плоскости
5. Прямая линия на плоскости. Уравнение прямой с угловым коэффициентом
6. Общее уравнение прямой
7. Угол между прямыми
8. Условия параллельности и перпендикулярности прямых
9. Уравнение прямой, проходящей через заданную точку в заданном направлении
10. Уравнение прямой, проходящей через две заданные точки
11. Уравнение окружности
12. Определители второго порядка
13. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения
14. Методы вычисления определителей третьего порядка
15. Решение систем линейных уравнений по формулам Крамера
16. Матрицы. Основные определения. Сложение и умножение матриц
17. Обратная матрица и ее вычисление
18. Решение системы линейных уравнений с помощью обратной матрицы
19. Векторы. Действия над ними. Скалярное произведение векторов.
20. Условия параллельности и перпендикулярности двух векторов.
21. Общее уравнение плоскости и его исследование.
22. Уравнение плоскости, проходящей через три данные точки.
23. Условия параллельности и перпендикулярности плоскостей.
24. Расстояние от точки до плоскости.
25. Прямая линия в пространстве. Канонические уравнения прямой.
Часть 2. Математический анализ. Элементы теории вероятностей.1. Основные элементарные функции их свойства и графики.
2. Определение производной функции в точке. Таблица производных.
3. Правила дифференцирования.
4. Производная сложной функции.
5. Промежутки возрастания и убывания функции. Максимум и минимум функции.
6. Наибольшее и наименьшее значения функции на отрезке.
7. Первообразная. Неопределенный интеграл.
8. Свойства неопределённого интеграла.
9. Таблица неопределённых интегралов.
10. Определение и свойства определенного интеграла.
11. Геометрический смысл определенного интеграла.
12. Формула Ньютона–Лейбница.
13. Вычисление площадей плоских фигур с помощью определенного интеграла.
14. Ряды. Необходимый признак сходимости числовых рядов.
15. Дифференциальные уравнения первого порядка.
16. Классическое и статистическое определения вероятности события.
17. Теоремы сложения вероятностей.
18. Теоремы умножения вероятностей.
19. Формула Бернулли.
20. Дискретные случайные величины. Закон распределения.
21. Математическое ожидание и дисперсия дискретной случайной величины.
22. Предмет и задачи математической статистики. Генеральная и выборочная совокупность.
23. Вариационный ряд. Статистическое распределение выборки.
24. Полигон частот. Гистограмма частот.
25. Точечные и интервальные оценки параметров распределения.
Формат и содержание экзамена, критерии оценки. Экзамен проводится в установленное расписанием время по утвержденным билетам. Билет содержит два теоретических вопроса и одно практическое задание. Практическое задание оформляется в письменном виде со всеми необходимыми комментариями по алгоритму решения. На теоретические вопросы студент отвечает устно. Для получения оценки «Отлично» необходимо правильно решить практическое задание, знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Хорошо» необходимо знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Удовлетворительно» необходимо уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы Перечень рекомендуемой литературыОсновная литература:
1. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике (в двух частях) – М.: Финансы и статистика, 2005.
2. Шипачев В.С. Основы высшей математики. – М.: Высшая школа, 2006.
3. Краснов М.А. и др. Вся высшая математика (в шести томах). – М.: Эдиториал УРСС, 2000.
4. Кремер Н.Ш. и др. Высшая математика для экономистов. – М.: ЮНИТИ, 2002.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2006.
Дополнительная литература:
6. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов. – М.: ЮНИТИ, 2002.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 2006.
8. Коровина Л.А. Математика (Элементы аналитической геометрии, линейной алгебры и линейного программирования): Методическое пособие по изучению курса и выполнению расчетных работ для студентов, обучающихся по специальности «Туризм». М.: МАТГР, 2007.
9. Коровина Л.А. Математика (дифференциальное и интегральное исчисления). Учебно-методическое пособие по изучению курса и выполнению расчётных работ. М.: МГИИТ, 2010.
Организационно – учебные нормы
| Название контрольной точки | Срок сдачи | Срок проверки |
| Первое задание – выполнить контрольную работу | За одну неделю до весенней сессии (не позднее) | В течение одной недели после сдачи |
| Второе задание – сдать экзамен | Весенняя сессия |
Оформленные задания в рукописном виде на листах формата А4 или в тетради в клеточку сдавать на кафедру информационных технологий и математики (к. 208) до указанного срока с записью в журнале контрольных заданий.
Тематический план изучения дисциплины, 1 семестр
| Тема | Виды учебных занятий | |||
| Всего | Ауд. работа | Самостоятельные занятия | ||
| Лекции | Семинар | |||
| Первый семестр Раздел 1. Элементы аналитической геометрии | ||||
| Аналитическая геометрия на плоскости. Метод координат. Расстояние между двумя точками. Деление отрезка в данном отношении. | ||||
| Прямая на плоскости. Угловой коэффициент прямой. Уравнение первой степени. Угол между прямыми. Условия параллельности и перпендикулярности прямых. | ||||
| Раздел 2. Определители. Матрицы. Решение систем линейных уравнений | ||||
| Определители второго и третьего порядка. Их свойства. Миноры и алгебраические дополнения. Методы вычисления определителей. | ||||
| Решение и исследование систем трех линейных уравнений с тремя неизвестными. Формулы Крамера. | ||||
| Матрицы. Действия над матрицами. Обратная матрица и ее вычисление. Решение системы линейных уравнений с помощью обратной матрицы. | ||||
| Раздел 3. Дифференциальное и интегральное исчисление. Элементы теории рядов | ||||
| Производные и дифференциалы функции одной переменной. Геометрический и физический смысл производной. Приложения производной. Максимум и минимум функций. Наибольшее и наименьшее значения функций на отрезке. | ||||
| Интегральное исчисление. Первообразная. Определенный интеграл и его геометрический смысл. Приложения определенного интеграла. Ряды. Необходимый признак сходимости ряда. Дифференциальные уравнения первого порядка. Уравнения в полных дифференциалах. Линейные дифференциальные уравнения второго порядка. | ||||
| Раздел 4. Элементы теории вероятностей, математической статистики и теории массового обслуживания | ||||
| Теория вероятностей. Формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей. Схема Бернулли. Случайные величины и их числовые характеристики. | ||||
| Элементы математической статистики. Статистическое распределение выборки. Полигон и гистограмма. Точечные и интервальные оценки параметров распределения. Понятие о статистических критериях. Основы теории массового обслуживания. Входящие потоки. Основные характеристики (длина очереди, периоды занятости, время ожидания). Типы систем обслуживания. Оптимизационные задачи теории массового обслуживания. | Экз.36 | |||
| Всего часов: |
Каждый студент должен решить 8 задач своего варианта. Номер варианта совпадает с последней цифрой учебного номера (шифра) студента. Например, для варианта №6 следует решить задачи №№ 6, 16, 26, 36, 46, 56, 66, 76; для варианта №0 следует решить задачи №№ 10, 20, 30, 40, 50, 60, 70, 80.
1–10. Даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
1. А (–5; 0), В (7; 9), C (5; –5).
2. A (–7; 2), B (5; 11), С (3; –3).
3. А (–5; –3), В (7; 6), C (5; –8).
4. А (–6; –2), В (6; 7), C (4; –7).
5. А ( –8; –4), В (4; 5), C (2; –9).
6. А (0; –1), В (12; 8), С (10; –6).
7. А (–6; 1), В (6; 10), С (4; –4).
8. А (–2; –4), В (10; 5), С (8; –9).
9. А (–3; 0), В (9; 9), С (7; –5).
10. А (–9; –2), В (3; 7), С (1; –7).
11–20. Решить данную систему уравнений с помощью формул Крамера. Сделать проверку полученного решения.
11. 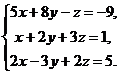 12.
12. 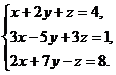
13. 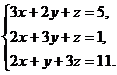 14.
14. 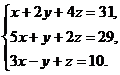
15. 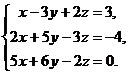 16.
16. 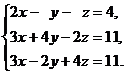
17. 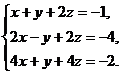 18.
18. 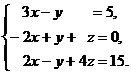
19. 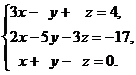 20.
20. 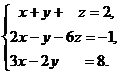
21–30. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
21. 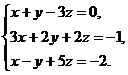 22.
22. 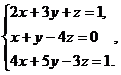
23. 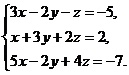 24.
24. 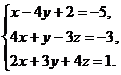
25. 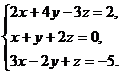 26.
26. 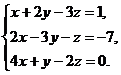
27. 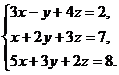 28.
28. 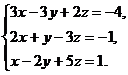
29. 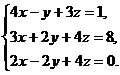 30.
30. 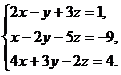
31-40. Исследовать функцию y = f(x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f(x) на отрезке [a, b].
31. 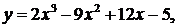 a = - 1 , b = 3
a = - 1 , b = 3
32. 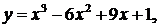 a = - 1 , b = 2
a = - 1 , b = 2
33. 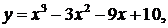 a = 2 , b = 3
a = 2 , b = 3
34. 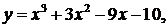 a = - 1 , b = 2
a = - 1 , b = 2
35. 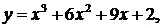 a = 0 , b = 4
a = 0 , b = 4
36. 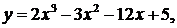 a= - 2 , b= 3
a= - 2 , b= 3
37. 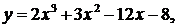 a = - 3 , b = 0
a = - 3 , b = 0
38. 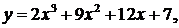 a = -3 , b = 1
a = -3 , b = 1
39. 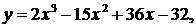 a = 1 , b = 4
a = 1 , b = 4
40. 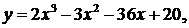 a = - 1 , b = 4
a = - 1 , b = 4
41-50. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.
41. 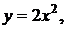
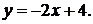
42. 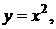
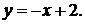
43. 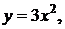
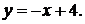
44. 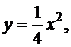
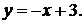
45. 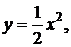
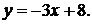
46. 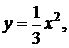
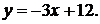
47. 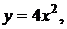
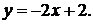
48. 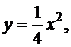
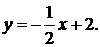
49. 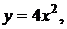
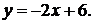
50. 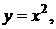
51–60. В ящике содержится n одинаковых, тщательно перемешанных шаров, причем k из них – красные, l – синие и m – белые. Наудачу вынимается один шар. Найти вероятность того, что вынутый шар а) синий, б) белый, в) цветной.
51. n = 8, k = 3, l = 3, m = 2.
52. n = 9, k = 4, l = 1, m = 4.
53. n = 10, k = 3, l = 5, m = 2.
54. n = 11, k = 5, l = 3, m = 3.
55. n = 12, k = 4, l = 6, m = 2.
56. n = 8, k = 1, l = 5, m = 2.
57. n = 9, k = 3, l = 4, m = 2.
58. n = 10, k = 2, l = 7, m = 1.
59. n = 11, k = 2, l = 4, m = 5.
60. n = 12, k = 3, l = 5, m = 4.
61–70. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения.
61.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
62.
| xi | ||||
| pi | 0,5 | 0,1 | 0,3 | 0,1 |
63.
| xi | ||||
| pi | 0,1 | 0,2 | 0,3 | 0,4 |
64.
| xi | ||||
| pi | 0,6 | 0,1 | 0,1 | 0,2 |
65.
| xi | ||||
| pi | 0,3 | 0,2 | 0,1 | 0,4 |
66.
| xi | ||||
| pi | 0,1 | 0,3 | 0,1 | 0,5 |
67.
| xi | ||||
| pi | 0,1 | 0,2 | 0,4 | 0,3 |
68.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
69.
| xi | ||||
| pi | 0,6 | 0,2 | 0,1 | 0,1 |
70.
| xi | ||||
| pi | 0,3 | 0,2 | 0,4 | 0,1 |
71–80. Известны математическое ожидание a и среднеквадратическое отклонение s нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал (a; b).
71. a = 11, s = 5, a = 5, b = 10.
72. a = 10, s = 4, a = 6, b = 11.
73. a = 9, s = 1, a = 7, b = 12.
74. a = 8, s = 2, a = 4, b = 10.
75. a = 7, s = 3, a = 4, b = 12.
76. a = 6, s = 5, a = 4, b = 8.
77. a = 5, s = 2, a = 2, b = 7.
78. a = 4, s = 3, a = 1, b = 9.
79. a = 3, s = 2, a = 3, b = 8.
80. a = 2, s = 1, a = 1, b = 4.
Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.