Методы вычисления пределов функции.
Определение: Пусть функция 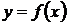 определена в некоторой проколотой окрестности точки а. Если она непрерывна в точке а, то назовем ее значение в точке
определена в некоторой проколотой окрестности точки а. Если она непрерывна в точке а, то назовем ее значение в точке 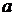 пределом функции
пределом функции 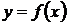 при стремлении х к а и будем писать
при стремлении х к а и будем писать
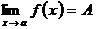 .
.
Если функция 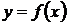 разрывна в точке
разрывна в точке 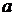 , то может случиться, что этот разрыв устранимый. Тогда можно изменить значение функции в точке
, то может случиться, что этот разрыв устранимый. Тогда можно изменить значение функции в точке 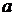 или доопределить ее в этой точке так, что в результате получится функция, непрерывная в точке
или доопределить ее в этой точке так, что в результате получится функция, непрерывная в точке 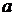 .
.
Примеры:
1.Вычислить 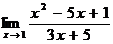 .
.
Т.к. функция 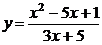 непрерывна в точке
непрерывна в точке 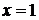 , то предел функции при
, то предел функции при 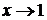 , равен ее значению в этой точке, т.е.
, равен ее значению в этой точке, т.е.
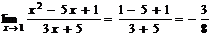 .
.
2.Вычислить 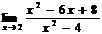 .
.
Здесь нельзя воспользоваться рассуждением предыдущего примера, поскольку функция 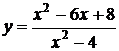 не определена, а значит, разрывна в точке
не определена, а значит, разрывна в точке 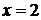 . Выполним некоторые преобразования аналитического выражения этой функции:
. Выполним некоторые преобразования аналитического выражения этой функции:
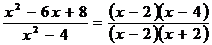 .
.
В проколотой окрестности точки 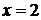 функция
функция 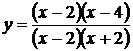
совпадает с функцией 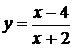 , непрерывной в этой точке и принимающей в ней значение
, непрерывной в этой точке и принимающей в ней значение 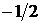 . Таким образом
. Таким образом
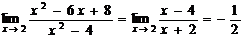 .
.
Основные теоремы о пределах
Теорема 1. Если каждое слагаемое алгебраической суммы конечного числа функций имеет предел при 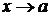 , то предел этой алгебраической суммы при
, то предел этой алгебраической суммы при 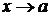 существует и равен такой же алгебраической сумме пределов слагаемых.
существует и равен такой же алгебраической сумме пределов слагаемых.
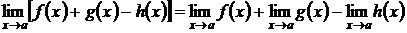 .
.
Терема 2. Если каждый из сомножителей произведения конечного числа функций имеет предел при 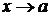 , то предел произведения при
, то предел произведения при 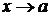 равен произведению пределов сомножителей.
равен произведению пределов сомножителей.
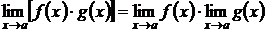 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела.
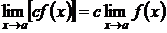 .
.
Следствие 2.Если функция 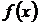 имеет предел при
имеет предел при 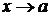 , то предел при
, то предел при 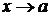 целой положительной степени ее равен такой же степени предела этой функции, т.е.
целой положительной степени ее равен такой же степени предела этой функции, т.е.
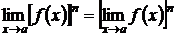 ,(n – натуральное число).
,(n – натуральное число).
Теорема 3. Если функция 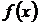 имеет предел при
имеет предел при 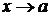 , отличный от нуля, то предел при
, отличный от нуля, то предел при 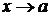 обратной ей по величине функции
обратной ей по величине функции 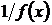 равен обратной величине предела данной функции, т.е.
равен обратной величине предела данной функции, т.е.
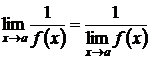 .
.
Теорема 4. Если делимое 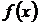 и делитель
и делитель 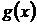 имеют пределы при
имеют пределы при 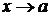 и предел делителя отличен от нуля, то предел их частного (дроби) при
и предел делителя отличен от нуля, то предел их частного (дроби) при 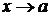 равен частному пределов делимого (числителя дроби) и делителя (знаменателя дроби), т.е.
равен частному пределов делимого (числителя дроби) и делителя (знаменателя дроби), т.е.
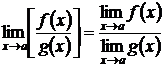 .
.
Теорема 5. Если функция 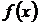 имеет предел при
имеет предел при 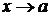 и
и 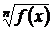
(n – натуральное число) существует в точке 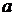 и в некоторой ее окрестности, то
и в некоторой ее окрестности, то
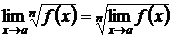 .
.
Решение типовых заданий
Пример 1. Найти: а) 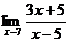 ; б)
; б) 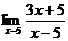 ; в)
; в) 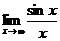 ; г)
; г) 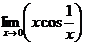 .
.
Р е ш е н и е: а) На основании непрерывности функции в точке х=7 искомый предел равен значению функции в этой точке, т.е. 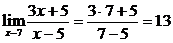 .
.
б) При 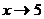 числитель (3х+5) стремится к
числитель (3х+5) стремится к 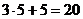 (т.е. является ограниченной функцией), а знаменатель (х-5) – к нулю (т.е. является бесконечно малой величиной); очевидно, их отношение есть величина бесконечно большая, т.е.
(т.е. является ограниченной функцией), а знаменатель (х-5) – к нулю (т.е. является бесконечно малой величиной); очевидно, их отношение есть величина бесконечно большая, т.е. 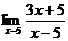 =
= 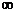 .
.
в) 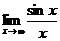 =0, ибо отношение ограниченной функции sinx
=0, ибо отношение ограниченной функции sinx 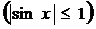 к бесконечно большой величине х (при
к бесконечно большой величине х (при 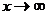 ) есть величина бесконечно малая.
) есть величина бесконечно малая.
г) 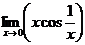 =0, т.к. произведение бесконечно малой величины х (при
=0, т.к. произведение бесконечно малой величины х (при 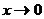 ) на ограниченную функцию
) на ограниченную функцию 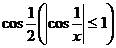 есть величина бесконечно малая.
есть величина бесконечно малая.
Заметим, что этот предел нельзя вычислять с помощью теоремы о пределе произведения, поскольку 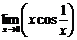 не существует (при
не существует (при 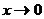 аргумент косинуса
аргумент косинуса  изменяется непрерывно вдоль числовой оси до бесконечности, при этом значения
изменяется непрерывно вдоль числовой оси до бесконечности, при этом значения 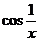 колеблются от -1 до 1 и от 1 до -1, не стремясь ни к какому числу (пределу).
колеблются от -1 до 1 и от 1 до -1, не стремясь ни к какому числу (пределу).
В рассмотренных примерах предел находится сразу: в виде числа или символа 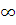 . Но чаще при вычислении пределов мы сталкиваемся с неопределенностями, когда результат нахождения предела неясен: например, в случае отношения двух бесконечно малых функций (условное обозначение
. Но чаще при вычислении пределов мы сталкиваемся с неопределенностями, когда результат нахождения предела неясен: например, в случае отношения двух бесконечно малых функций (условное обозначение 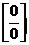 ) или бесконечно больших
) или бесконечно больших 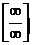 . Кроме отмеченных неопределенностей вида
. Кроме отмеченных неопределенностей вида 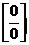 и
и 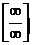 в математическом анализе рассматриваются также неопределенности вида
в математическом анализе рассматриваются также неопределенности вида 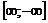 ,
, 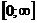 ,
, 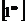 ,
, 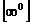 ,
, 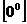 .
.
Пример 2.Найти:
а) 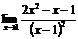 ; б)
; б) 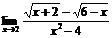 ; в)
; в) 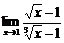 .
.
Р е ш е н и е: а) для раскрытия неопределенности вида 
Разложим числитель на множители и сократим дробь множитель (х-1): сокращение возможно, т.к. при 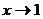 (х-1) стремится к нулю, но не равен нулю.
(х-1) стремится к нулю, но не равен нулю.
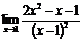 =
=  =
= 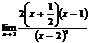 =
= 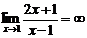 .
.
б) Для раскрытия неопределенности вида  умножим числитель и знаменатель на выражение, сопряженное к числителю, получим:
умножим числитель и знаменатель на выражение, сопряженное к числителю, получим:
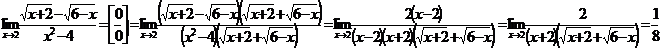 в) Для раскрытия неопределенности вида
в) Для раскрытия неопределенности вида 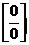 удобно предварительно сделать замену
удобно предварительно сделать замену 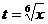 (тогда
(тогда 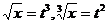 , при
, при 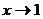 ), а затем полученные многочлены разложить на множители:
), а затем полученные многочлены разложить на множители: 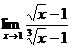 =
= 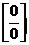 =
= 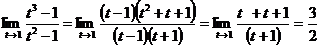 .
.
Пример 3.Найти: а) 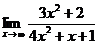 ; б)
; б) 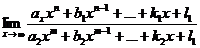 ;
;
в) 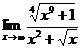 ; г)
; г) 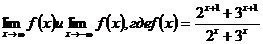 ; д)
; д) 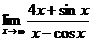 .
.
Р е ш е н и е: а) Имеем неопределенность вида 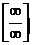 . Учитывая, что поведение числителя и знаменателя при
. Учитывая, что поведение числителя и знаменателя при 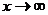 определяется членами с наибольшими показателями степеней (соответственно
определяется членами с наибольшими показателями степеней (соответственно 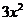 и
и 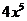 ), разделим числитель и знаменатель на
), разделим числитель и знаменатель на 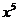 , т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим:
, т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим:
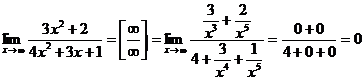 .
.
б) Используя тот же прием, что и в п.а), можно показать, что
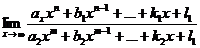 =
= 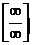 =
= 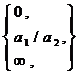 , т.е. предел отношения двух многочленов
, т.е. предел отношения двух многочленов 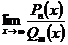 равен 0, отношению коэффициентов при старших степенях х или
равен 0, отношению коэффициентов при старших степенях х или 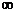 , если показатель степени числителя и соответственно меньше, равен или больше показателя степени знаменателя m.
, если показатель степени числителя и соответственно меньше, равен или больше показателя степени знаменателя m.
Рекомендуем запомнить это правило.
в) Имеем неопределенность вида 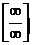 . Здесь выражению в числителе условно можно приписать степень
. Здесь выражению в числителе условно можно приписать степень 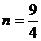 , а в знаменателе степень m=2; т.к.
, а в знаменателе степень m=2; т.к. 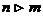 , то на основании правила, сформулированного в п.б), искомый предел равен
, то на основании правила, сформулированного в п.б), искомый предел равен 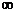 .
.
Действительно, разделив и числитель и знаменатель на 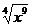 , получим:
, получим:
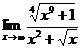 =
= 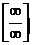 =
= 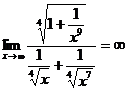 .
.
г) При 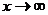 имеем неопределенность вида
имеем неопределенность вида 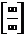 , при этом поведение числителя и знаменателя определяется вторыми слагаемыми, которые возрастают быстрее первых. Разделив числитель и знаменатель на
, при этом поведение числителя и знаменателя определяется вторыми слагаемыми, которые возрастают быстрее первых. Разделив числитель и знаменатель на 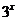 и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим:
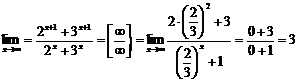 , поскольку
, поскольку 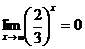 .
.
При 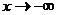 имеем неопределенность вида
имеем неопределенность вида  , при этом поведение числителя и знаменателя определяется первыми слагаемыми, которые убывают медленнее других. Разделив числитель и знаменатель на
, при этом поведение числителя и знаменателя определяется первыми слагаемыми, которые убывают медленнее других. Разделив числитель и знаменатель на 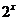 и используя теоремы о пределах, получим:
и используя теоремы о пределах, получим:
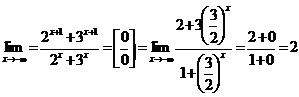 .
.
д) Для раскрытия неопределенности вида 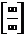 разделим числитель на x, получим
разделим числитель на x, получим
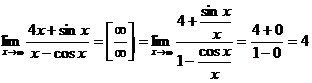
так как 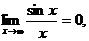
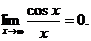
Пример 4. Найти:
а) 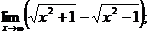
б) 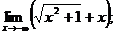
в) 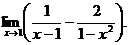
Решение: а) Для раскрытия неопределенности вида 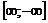 умножим и разделим выражение в скобках на сопряжение выражение, получим
умножим и разделим выражение в скобках на сопряжение выражение, получим
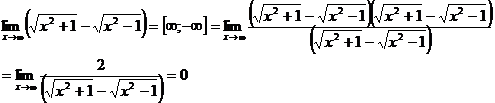
б) При 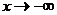 имеем неопределенность вида
имеем неопределенность вида 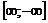 , ибо квадратный корень из неотрицательного числа всегда неотрицателен.
, ибо квадратный корень из неотрицательного числа всегда неотрицателен.
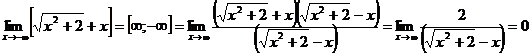
Обращаем внимание на то, что при x → 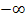 в знаменателе нет неопределенности, так как он представляет сумму бесконечно больших положительных величин – величину, бесконечно большую.
в знаменателе нет неопределенности, так как он представляет сумму бесконечно больших положительных величин – величину, бесконечно большую.
в) 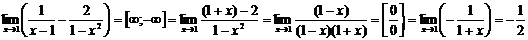
Пример 5.Вычислить пределы числовых последовательностей.
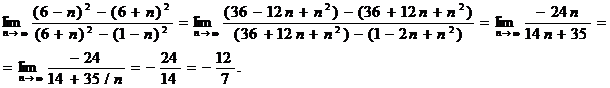
Пример 6.Вычислить пределы числовых последовательностей.
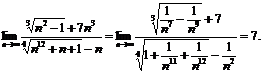
Пример 7 .Вычислить пределы функций.
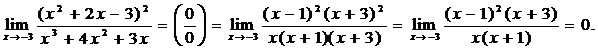
Пример 8 .Вычислить пределы функций.
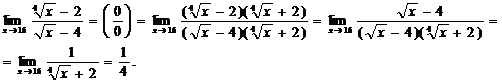
Пример 9 .Вычислить пределы функций.
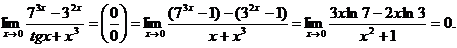
Пример 10.Вычислить пределы функций.
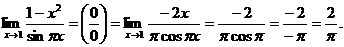
Пример 11.Вычислить пределы функций.
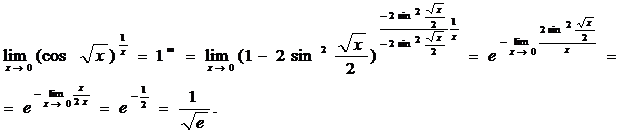
Пример 12.Вычислить пределы функций.
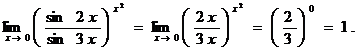
Пример 13.Вычислить пределы функций.
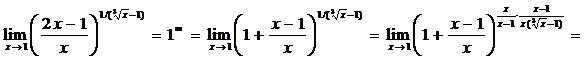
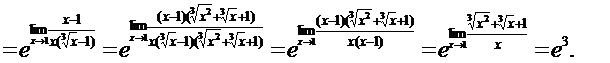
Пример 14.Вычислить пределы функций.
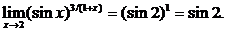
Упражнения и задания для самостоятельной работы
Теоретические вопросы
- Что называется пределом числовой последовательности?
- Что такое бесконечно малая (бесконечно большая) величина?
- Какие свойства пределов числовых последовательностей используют при вычислении пределов?
- Что такое предел функции в точке?
- Какие свойства пределов функций используются при вычислении пределов?
- Что такое I (II) замечательный предел?
