Тема №14 «Дисперсионный анализ»
Цель:научиться применять однофакторный дисперсионный анализ для проверки гипотезы о равенстве математических ожиданий нескольких нормально распределённых генеральных совокупностей.
Краткие теоретические сведения:
Дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор 
, который имеет 
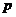уровней 
на изучаемую величину 
. Или, фактически, проверяют гипотезу о равенстве математических ожиданий наблюдаемых значений на каждом из уровней.
Идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порожденной воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами.
Если различия между дисперсиями значимо, то фактор оказывает существенное влияние на , в этом случае математические ожидания наблюдаемых значений на каждом уровне (групповые средние) различаются также значительно.
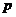Пусть на действует фактор , который имеет постоянных уровней. Будем предполагать, что число наблюдений (испытаний) на каждом уровне равно 
. Тогда наблюдалось 
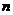значений 
признака , где 
– номер испытания, 
– номер уровня фактора.
Результаты наблюдений оформляются в виде таблицы:
| № испытания | Уровни фактора  | |||
 |  | … |  | |
…  |   …  |   …  | … … … … |   …  |
Далее рассчитываем остаточную и факторную дисперсии по формулам:
,
, 
,
, 
.
Гипотеза о значимости фактора принимается, если 
, где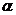 
уровень значимости, 
и отвергается, если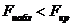 
(смотрите тему о сравнении двух дисперсий нормальных генеральных совокупностей).
Пример. Произведено 10 испытаний, из них 4 на первом уровне фактора, 4 – на втором и 2 – на третьем.
| № испытания | Уровни фактора | ||
| | | | |
Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве математических ожиданий. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
Решение.
44942-40960=3982,
=44272-40960=3312,
Qост=3982-3312=670.
S2факт= 
, S2ост= 
.
, 
.
Так как Fнабл>Fкр – нулевую гипотезу о равенстве математических ожиданий отвергаем, следовательно, принимаем гипотезу о значимости фактора.
Контрольные вопросы:
1. Постановка задачи дисперсионного анализа.
2. Факторная и остаточная дисперсии.
3. Проверка гипотезы о равенстве математических ожиданий нескольких генеральных совокупностей методом дисперсионного анализа.
4. Двухфакторный дисперсионный анализ.
5. Дисперсионные модели.
Контрольные задания:
1. Произведено по 4 испытания на каждом из трёх уровней. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве математических ожиданий. Предполагается, что выборки извлечены из нормальных генеральных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| | | |  |
2. Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве математических ожиданий. Предполагается, что выборки извлечены из нормальных генеральных совокупностей с одинаковыми дисперсиями.
| Номер испытания | Уровни фактора | ||
| | | | |
3. В четырёх экспериментальных центрах проверялись три методики тестирования. Данные об успешности тестирования приведены в таблице. Требуется при уровне значимости 0,05 проверить влияние на успешность тестирования методик (фактор А) и экспериментальных центров (фактор В).
| А1 | А2 | А3 | |||||||
| В1 | |||||||||
| В2 | |||||||||
| В3 | |||||||||
| В4 |
Задания для домашней работы:
При уровне значимости 0,05 проверить нулевую гипотезу о равенстве математических ожиданий. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми генеральными дисперсиями.
| Номер испытания | Уровни фактора | ||||
| | | | |  |  |