Тема №11 «Построение статистических рядов, нахождение их характеристик»
Цель:научиться составлять статистические распределения выборок, строить полигоны, гистограммы, строить эмпирические функции распределения.
Краткие теоретические сведения:
Математическая статистика– это раздел прикладной математики, посвящённый методам сбора, группировки и анализа статистических сведений, полученных в результате наблюдений или экспериментов.
Генеральной совокупностью называют множество объектов, однородных относительно некоторого признака.
Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Число объектов совокупности называется её объёмом.
Выборка называется репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности, и если все объекты имеют одинаковую вероятность попасть в выборку.
Численное значение количественного признака называется вариантой.
Статистическим распределением выборки называют перечень вариант  и соответствующих им частот
и соответствующих им частот 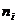 или относительных частот
или относительных частот  .
.
Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариант с соответствующими им частотами.
Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и – интервальным, если варианты могут отличаться одна от другой на сколь угодно малую величину.
Дискретный статистический ряд задается таблицей, в которой указываются варианты, частоты или относительные частоты их встречаемости. Графическое изображение дискретного статистического ряда называетсяполигоном частот (относительных частот).Это ломаная, в которой концы отрезков имеют координаты 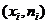 или
или  ,
, 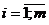 .
.
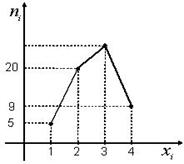
Пример. Закон распределения дискретного статистического рядя и полигон частот.
 | ||||
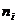 |
Интервальный статистический ряд для случайных непрерывных величин и для случайных дискретных величин при больших объемах выборок. Интервальный ряд представляет собой таблицу, в которой указаны частичные интервалы, плотности частот или плотности относительных частот. Графическое изображение интервального статистического ряда называетсягистограммой.Представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака, и высотами, равными частотам интервалов.
Пример. Закон распределения интервального статистического ряда и гистограмма.
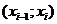 | (55;60) | (60;65) | (65;70) | (70;75) | (75;80) | (80;85) | (85;90) |
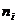 |

Алгоритм построения интервального ряда:
Пусть дана выборка 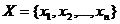 с объёмом
с объёмом 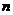 .
.
1) находим размах выборки 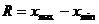 ,
,
2) определяем число классов разбиения по формулам:
 (формула Стерджесса для
(формула Стерджесса для 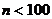 )
)
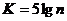 (формула Брукса для
(формула Брукса для 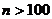 ),
),
3) находим величину классового интервала 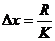 ,
,
4) границы частичных интервалов находим по формулам:
 ,
,  ,
,  ,
,  .
.
 |
5) подсчитываем частоты попадания вариант в каждый интервал.
Кумулятивная кривая (кумулята) – кривая накопленных частот. Для дискретного ряда кумулята представляет собой ломаную, соединяющую точки 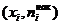 или
или  ,
, 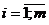 . Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината накопленной частоте, равной 0. Другие точки соответствуют концам интервалов.
. Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината накопленной частоте, равной 0. Другие точки соответствуют концам интервалов.
Эмпирической функцией распределения 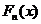 называется относительная частота того, что признак примет значение, меньшее заданного
называется относительная частота того, что признак примет значение, меньшее заданного 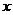 , то есть
, то есть  .
.
Для дискретного вариационного ряда эмпирическая функция представляет собой разрывную ступенчатую функцию, для интервального – совпадает с кумулятой.


Основные числовые характеристики вариационного ряда:
Среднее арифметическое вариационного ряда  , где
, где  - варианты дискретного ряда или середины интервалов интервального,
- варианты дискретного ряда или середины интервалов интервального, 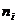 - соответствующие им частоты.
- соответствующие им частоты.
Основные свойства средней арифметической:
1) 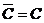 ,
,
2) 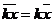 ,
,
3)  ,
,
4) 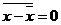 ,
,
5)  ,
,
6)  , где
, где  - общая средняя,
- общая средняя,  - групповая средняя
- групповая средняя  -той группы с объёмом
-той группы с объёмом 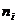 ,
, 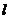 - число групп.
- число групп.
Дисперсия вариационного ряда 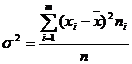 .
.
Основные свойства дисперсии:
1)  ,
,
2) 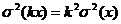 ,
,
3) 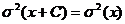 ,
,
4) 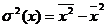 ,
,
5)  , где
, где 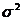 - общая дисперсия,
- общая дисперсия, 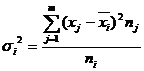 - групповая дисперсия,
- групповая дисперсия, 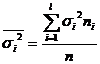 - средняя арифметическая групповых дисперсий,
- средняя арифметическая групповых дисперсий,  - межгрупповая дисперсия.
- межгрупповая дисперсия.
6)  - дисперсия среднего значения.
- дисперсия среднего значения.
Среднее квадратическое отклонение  .
.
Коэффициент вариации  .
.
Медиана вариационного ряда 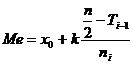 , где
, где  - начало медианного интервала,
- начало медианного интервала,  - его длина,
- его длина, 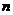 - объём выборки,
- объём выборки, 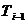 - сумма частот интервалов, предшествующих медианному,
- сумма частот интервалов, предшествующих медианному, 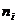 - частота медианного интервала. Для дискретного ряда медиана - значение признака, приходящееся на середину ранжированного ряда наблюдений.
- частота медианного интервала. Для дискретного ряда медиана - значение признака, приходящееся на середину ранжированного ряда наблюдений.
Мода 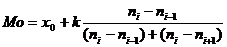 , где
, где  - начало модального интервала,
- начало модального интервала,  - его длина,
- его длина, 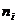 - частота модального интервала,
- частота модального интервала, 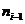 и
и  - частоты соответственно предшествующего и последующего за модальным интервалов. Для дискретного ряда мода - варианта, которой соответствует наибольшая частота.
- частоты соответственно предшествующего и последующего за модальным интервалов. Для дискретного ряда мода - варианта, которой соответствует наибольшая частота.
Начальный момент  -го порядка
-го порядка  .
.
Центральный момент  -го порядка
-го порядка 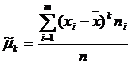 .
.
Коэффициент асимметрии  .
.
Эксцесс 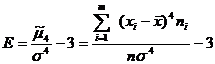 .
.
Контрольные вопросы:
1. Генеральная и выборочная совокупности, их объём.
2. Статистическое распределение выборки. Вариационный ряд.
3. Дискретный статистический ряд. Полигон частот.
4. Интервальный статистический ряд. Гистограмма.
5. Алгоритм построения интервального статистического ряда.
6. Эмпирическая функция распределения. Кумулятивная кривая.
7. Среднее арифметическое вариационного ряда и его свойства.
8. Дисперсия и её свойства. СКО.
Контрольные задания:
1.Как известно, почерк человека, в том числе наклон букв, тесно связан с его характером. Низкий наклон (30 – 40 град.) свидетельствует о вспыльчивости и возбудимости человека, излишней прямоте и торопливости в поступках; наклон 40 – 50 град. характеризует гармоническое развитие натуры; наклон 50 – 90 град. свидетельствует о самообладании, узком диапазоне увлечений.
Среди студентов института выборочно был исследован почерк 50 человек. Оказалось, что почерк у 30% присутствующих имеет низкий наклон, у 50% - наклон 40 – 50 и у 20% - наклон 50 – 90 град.
Найти распределение частот, относительных частот, построить полигон и гистограмму.
2. Дано распределение признака  , полученное по
, полученное по 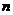 наблюдениям. Необходимо:
наблюдениям. Необходимо:
1) построить (полигон) гистограмму, кумуляту и эмпирическую функцию распределения;
2) найти: среднюю арифметическую, моду и медиану, дисперсию, СКО и коэффициент вариации, начальные и центральные моменты  -го порядка.
-го порядка.
а)
 | |||||||||||
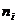 |
б)
 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 | 20-22 | 22-24 | 24-26 |
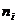 |
3. Вычислить общие и групповые средние и дисперсии и убедиться в справедливости правила сложения дисперсий.
 | группа 1 | группа 2 | ||||||||
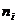 |
4. Изучался рост (см) мужчин возраста 25 лет. По случайной выборке объема 35: 175, 167, 168, 169, 168, 170, 174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173, 172, 166, 164, 168, 172, 174, найти статистический интервальный ряд распределения и построить гистограмму частот.
Задания для домашней работы:
Дано распределение признака  , полученное по
, полученное по 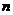 наблюдениям. Необходимо:
наблюдениям. Необходимо:
1) построить (полигон) гистограмму, кумуляту и эмпирическую функцию распределения;
2) найти: среднюю арифметическую, моду и медиану, дисперсию, СКО и коэффициент вариации, начальные и центральные моменты  -го порядка.
-го порядка.
а)
 | |||||
 |
б)
 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 |
 |
Тема №12 «Нахождение точечных и интервальных оценок параметров распределения»
Цель:научиться определять точечные и интервальные статистические оценки генеральных параметров нормального распределения по выборочным данным генеральной совокупности.
Краткие теоретические сведения:
Статистической оценкой (статистикой) неизвестного параметра q распределения генеральной совокупности называют функцию результатов наблюдений q*  .
.
Статистическая оценка q* является случайной величиной.
Оценка, определяемая одним числом, зависящим от выборочных данных, называется точечной.
Требования, предъявляемые к точечным статистическим оценкам:
1) состоятельность (стремление по вероятности к оцениваемому параметру при  ),
),
2) несмещённость (отсутствие систематических ошибок при любом объёме выборки 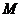 (q*) = q),
(q*) = q),
3) эффективность (среди всех возможных оценок эффективная оценка обладает наименьшей дисперсией).
Точечные оценки генеральных параметров нормально распределённой совокупности:
| Генеральный параметр | Точечная оценка |
 | 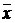 - выборочная средняя - выборочная средняя |
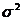 |  - исправленная дисперсия - исправленная дисперсия |
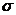 |  - исправленное среднеквадратическое отклонение - исправленное среднеквадратическое отклонение |
 | 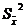 |
Интервальной оценкой называют оценку, которая определяется двумя числами – концами интервала.
Интервальные оценки позволяют установить точность и надёжность точечной оценки.
Точностью 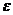 оценки называется отклонение по модулю q* от q.
оценки называется отклонение по модулю q* от q.
Предельной ошибкой выборки  называется максимально допустимое по модулю отклонение q* от q.
называется максимально допустимое по модулю отклонение q* от q.
Надёжностью (доверительной вероятностью) оценки q* называют вероятность 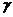 , с которой осуществляется неравенство |q - q*|<
, с которой осуществляется неравенство |q - q*|< 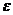 . Обычно
. Обычно 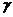 = 0,95; 0,99; 0,999…
= 0,95; 0,99; 0,999…
Вероятность того, что неизвестный параметр не попадёт в интервал |q - q*|< 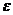 , равна
, равна  - уровню значимости.
- уровню значимости.
Доверительным называется интервал (q*- 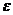 ;q*+
;q*+ 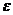 ), который покрывает неизвестный параметр с заданной надёжностью
), который покрывает неизвестный параметр с заданной надёжностью 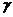 .
.
Интервальные оценки параметров нормального распределения:
1) Доверительный интервал для математического ожидания 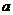 при известной дисперсии
при известной дисперсии 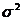 .
.
 , где
, где 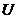 находят из таблицы функции Лапласа, учитывая
находят из таблицы функции Лапласа, учитывая 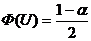 .
.
2) Доверительный интервал для математического ожидания 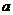 при неизвестной дисперсии
при неизвестной дисперсии 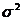 .
.
|
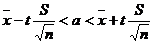 , где
, где 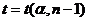 находят из таблицы коэффициентов Стьюдента.
находят из таблицы коэффициентов Стьюдента. 3) Доверительный интервал для дисперсии 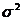 при известном
при известном 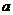 .
.
 <
< 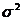 <
<  , где
, где 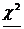 - находят из таблицы распределения
- находят из таблицы распределения 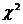 при 1-
при 1-  ,
,  - находят при
- находят при  с числом степеней свободы
с числом степеней свободы 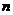 .
.
4) Доверительный интервал для дисперсии 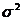 при неизвестном
при неизвестном 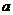 .
.
 , где
, где 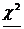 - находят из таблицы распределения
- находят из таблицы распределения 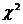 при 1-
при 1-  ,
,  - находят при
- находят при  с числом степеней свободы
с числом степеней свободы 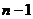 .
.
Пример 1. Вычислить несмещённые оценки параметров генеральной совокупности 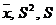 по выборочным данным: 64 63 71 68 73 71 74 73 70 75 68 67 73.
по выборочным данным: 64 63 71 68 73 71 74 73 70 75 68 67 73.
Решение.
 ,
,
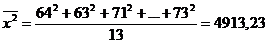 ,
,
 ,
,
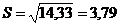 .
.
Пример 2. Найти доверительные интервалы для математического ожидания, дисперсии и стандартного отклонения при уровне значимости 0,05, если из генеральной совокупности сделана выборка, используемая в примере 1.
Решение. Используем данные из примера 1 для нахождения доверительного интервала для математического ожидания при неизвестной дисперсии:
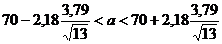 ,
,
где 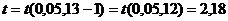
 .
.
Используем данные из примера 1 для нахождения доверительного интервала для дисперсии при неизвестном математическом ожидании:
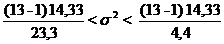 ,
,
где  =
= 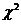 (
(  )=
)=  =4,4 и
=4,4 и  =
= 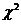

 ,
,
Контрольные вопросы:
1. Статистическая оценка неизвестного параметра теоретического распределения.
2. Точечная оценка.
3. Требования к точечным оценкам: несмещённость, состоятельность, эффективность.
4. Генеральная и выборочная средняя.
5. Генеральная и выборочная дисперсии.
6. Поправочный коэффициент. Исправленная выборочная дисперсия.
7. Генеральное среднеквадратическое отклонение и его точечная оценка.
8. Оценка дисперсии и СКО выборочной средней.
9. Интервальная оценка неизвестного параметра генеральной совокупности.
10. Доверительная вероятность и уровень значимости.
11. Доверительный интервал.
12. Правило нахождения доверительного интервала.
13. Доверительный интервал для математического ожидания 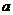 при известной дисперсии
при известной дисперсии 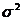 .
.
14. Доверительный интервал для математического ожидания 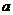 при неизвестной дисперсии
при неизвестной дисперсии 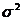 .
.
15. Доверительный интервал для дисперсии 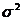 при известном
при известном 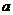 .
.
16. Доверительный интервал для дисперсии 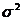 при неизвестном
при неизвестном 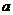 .
.
Контрольные задания:
1. При проверке успеваемости факультета были выборочно протестированы 50 обучаемых, распределившихся по результатам тестирования следующим образом (  - балл,
- балл, 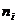 - количество обучаемых с данным баллом):
- количество обучаемых с данным баллом):
 | |||||
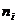 |
Найти средний балл.
2. Некто N собрал следующий статистический материал, касающийся дистанции при его общении с другими людьми в течение недели:
| Вид общения | Расстояние (см) | Относительная частота |
| Интимное | 0-45 | 0,3 |
| Персональное | 45-120 | 0,2 |
| Социальное | 120-400 | 0,1 |
| Публичное | 400-750 | 0,4 |
Найти выборочную среднюю дистанции общения.
3. Найти разброс среднего балла в задании 1 тестирования 50 студентов.
4. Найти оценку разброса скорости чтения, распределение, которой представлено в таблице, предварительно определив относительную частоту средней скорости чтения.
| Скорость слов в 1 мин | низкая | 250-300 средняя | 300-450 быстрая | сверхбыстрая |
| Относительная частота | 0,1 | ? | 0,4 | 0,05 |
5. Найти несмещённые оценки генеральной средней, дисперсии и среднеквадратического отклонения генеральной совокупности по выборке объема 12, описывающей продолжительность в секундах физической нагрузки до развития приступа стенокардии: 289, 208, 259, 243, 232, 210, 251, 246, 224, 239, 220, 211.
6. Имеется выборка объема  – это значения систолического давления у мужчин в начальной стадии шока: 127, 124, 155, 129, 77, 147, 65, 109, 145, 141. Определить дисперсию и среднеквадратическое отклонение выборочной средней.
– это значения систолического давления у мужчин в начальной стадии шока: 127, 124, 155, 129, 77, 147, 65, 109, 145, 141. Определить дисперсию и среднеквадратическое отклонение выборочной средней.
7. По схеме бесповторной выборки из 400 испытуемых в опытах Францена и Оффенлоха с применением вызванных потенциалов отобраны 100 человек и проведены замеры латентных периодов. Результаты испытаний приведены в таблице:
| Длительность латентного периода, мс | [40;42] | (42;44] | (44;46] | (46;48] | (48;50] | Итого |
| Количество испытуемых |
Задано среднее квадратическое отклонение  . Найти:
. Найти:
а) вероятность того, что средний латентный период всех 400 человек отличается от среднего периода в выборке не более чем на 0,31 мс (по абсолютной величине),
б) границы, в которых с вероятностью 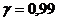 заключено среднее значение латентного периода,
заключено среднее значение латентного периода,
в) объём выборки, для которой доверительные границы с предельной ошибкой 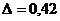 имели бы место с доверительной вероятностью
имели бы место с доверительной вероятностью 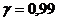 .
.
8. Распределение ежедневных визитов Карлсона к Малышу в течение месяца показано в таблице:
| Число визитов | ||||||
| Частота |
Определить границы, в которых с вероятностью 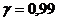 заключено среднее количество визитов.
заключено среднее количество визитов.
9. Случайная величина  имеет нормальное распределение с известным средним квадратическим отклонением
имеет нормальное распределение с известным средним квадратическим отклонением 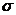 =3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним
=3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним  =24,5, если объём выборки
=24,5, если объём выборки  и задана надёжность оценки
и задана надёжность оценки 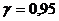 .
.
10. Количественный признак  генеральной совокупности распределён нормально. По выборке объёма
генеральной совокупности распределён нормально. По выборке объёма 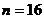 найдены выборочная средняя
найдены выборочная средняя  =20,2 и исправленное среднее квадратическое отклонение
=20,2 и исправленное среднее квадратическое отклонение 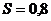 . Оценить неизвестное математическое ожидание при помощи доверительного интервала с надёжностью 0,95.
. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надёжностью 0,95.
11. Для 9 претендентов на должность руководителя была проведена оценка профессионального показателя 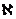 , характеризующего способность руководить людьми. Считая показатель
, характеризующего способность руководить людьми. Считая показатель 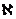 распределённым по нормальному закону со средним квадратическим отклонением
распределённым по нормальному закону со средним квадратическим отклонением  усл. ед., определить с надёжностью
усл. ед., определить с надёжностью 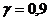 доверительный интервал для истинного среднего квадратического отклонения
доверительный интервал для истинного среднего квадратического отклонения 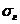 показателя
показателя 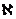 .
.
Задания для домашней работы:
1. Найти оценки генеральных средней, дисперсии и среднего квадратического отклонения, если совокупность задана таблицей распределения:
 | 6,76 | 6,78 | 6,80 | 6,82 | 6,84 |
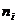 |
2. Вычислить несмещённые оценки параметров генеральной совокупности  по выборочным данным. По желанию можно составить вариационный ряд по значениям:
по выборочным данным. По желанию можно составить вариационный ряд по значениям:
71 71 69 74 75 70 78 66 69 74 81 73 74
3. Из генеральной совокупности извлечена выборка объема  :
:
 | -0,5 | -0,4 | -0,2 | 0,2 | 0,6 | 0,8 | 1,2 | 1,5 | ||
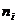 |
Оценить с надежностью 0,95 математическое ожидание нормально распределённого признака генеральной совокупности с помощью доверительного интервала.
4. Найти доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения при доверительной вероятности 0,95, если из генеральной совокупности сделана выборка:
67 70 69 68 74 72 66 66 74 69 72 78 67
Тема №13 «Проверка статистических гипотез о равенстве дисперсий и математических ожиданий»
Цель:научиться проверять статистические гипотезы о равенстве дисперсий и математических ожиданий нормальных генеральных совокупностей.
Краткие теоретические сведения:
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.
Нулевой (основной) называют выдвинутую гипотезу 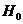 .
.
Конкурирующей (альтернативной) называют гипотезу 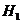 , которая противоречит нулевой.
, которая противоречит нулевой.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Вероятность совершить ошибку второго рода – уровень значимости 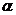 .
.
Статистическим критерием называют случайную величину  , которая служит для проверки нулевой гипотезы.
, которая служит для проверки нулевой гипотезы.
Наблюдаемым значением 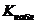 называют значение критерия, вычисленное по выборкам.
называют значение критерия, вычисленное по выборкам.
Критической областью называют совокупность значений критерия, при которой нулевую гипотезу отвергают.
Область принятия гипотезы – совокупность значений критерия, при котором гипотезу принимают.
Если 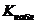 принадлежит критической области – гипотезу отвергают, если
принадлежит критической области – гипотезу отвергают, если 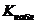 принадлежит области принятия гипотезы – гипотезу принимают.
принадлежит области принятия гипотезы – гипотезу принимают.
Критическими точками 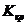 называют точки, отделяющие критическую область от области принятия гипотезы.
называют точки, отделяющие критическую область от области принятия гипотезы.
Критические точки ищут, исходя из требования, что при условии справедливости нулевой гипотезы, вероятность того, что критерий  попадет в критическую область, была равна принятому уровню значимости.
попадет в критическую область, была равна принятому уровню значимости.
Для каждого критерия имеются соответствующие таблицы, по которым находят критическую точку, удовлетворяющую этому требованию.
Когда 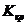 найдена, вычисляют по данным выборок
найдена, вычисляют по данным выборок 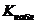 и, если
и, если 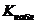 >
> 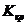 (правосторонняя критическая область),
(правосторонняя критическая область), 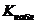 <
< 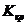 (левосторонняя),
(левосторонняя), 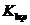 <
< 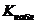 <
< 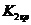 ,
, 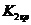 <
< 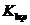 (двусторонняя), то
(двусторонняя), то 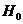 отвергается.
отвергается.
Сравнение двух дисперсий нормальных генеральных совокупностей:
Пусть  и
и 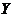 распространены нормально. По независимым выборкам с объемами, соответственно равными
распространены нормально. По независимым выборкам с объемами, соответственно равными 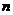 и
и 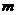 , извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии
, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии  и
и  . Требуется по исправленным дисперсиям при заданном уровне значимости
. Требуется по исправленным дисперсиям при заданном уровне значимости 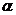 проверить нулевую гипотезу
проверить нулевую гипотезу  .
.
1) выдвигаем конкурирующую гипотезу  (
(  ),
),
2) находим  ,
,
3) по таблице критических точек Фишера –Снедекора находим 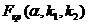 (
(  ), где
), где  ,
,  и
и  - объём выборки, которой соответствует
- объём выборки, которой соответствует 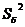 ,
,  -
- 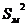 ,
,
4) если  , то принимаем нулевую гипотезу, в противном случае – альтернативную.
, то принимаем нулевую гипотезу, в противном случае – альтернативную.
Критерий Бартлетта. Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объема:
Пусть  распределены нормально. Из этих совокупностей извлечены независимые выборки различных объемов
распределены нормально. Из этих совокупностей извлечены независимые выборки различных объемов  . Найдены исправленные выборочные дисперсии
. Найдены исправленные выборочные дисперсии  . По уровню значимости
. По уровню значимости 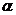 и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий
и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий 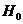 :
: 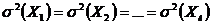 .
.
1) находим  , где
, где

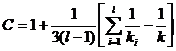
 ,
,
 ,
,
2) находим  по таблице критических точек
по таблице критических точек 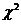 ,
,
3) если  , то принимаем нулевую гипотезу.
, то принимаем нулевую гипотезу.
Критерий Кочрена. Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема:
Пусть  распределены нормально. Из этих совокупностей извлечены независимые выборки одинакового объёма
распределены нормально. Из этих совокупностей извлечены независимые выборки одинакового объёма 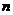 . Найдены исправленные выборочные дисперсии
. Найдены исправленные выборочные дисперсии  , все с одинаковым числом степеней свободы
, все с одинаковым числом степеней свободы  . По уровню значимости
. По уровню значимости 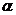 и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий
и исправленным выборочным дисперсиям проверить гипотезу об однородности дисперсий 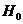 :
: 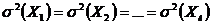 .
.
1) находим 
2) находим 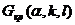 по таблице критических точек Кочрена,
по таблице критических точек Кочрена,
3) если  , то принимаем нулевую гипотезу.
, то принимаем нулевую гипотезу.
Сравнение двух математических ожиданий нормальных генеральных совокупностей, дисперсии которых известны:
Пусть  и
и 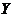 распределены нормально, их дисперсии известны. По выборкам объемов
распределены нормально, их дисперсии известны. По выборкам объемов 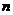 и
и 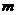 найдены выборочные средние
найдены выборочные средние  и
и  . По средним и
. По средним и
