И.р. хайбуллина, о.в. байгулова

И.Р. Хайбуллина, О.В. Байгулова

ВЫСШАЯ МАТЕМАТИКА

Учебно-МЕТОДИЧЕСКОЕ пособие

2-е издание, дополненное и переработанное

Уфа

БГМУ

УДК 510(022)

ББК

М

Рецензенты:

…профессор,

…профессор,

Высшая математика: учебно-методическое пособие / сост. И.Р. Хайбуллина, О.В. Байгулова. – Уфа: Изд. БГМУ, 2011. – … с.

ISBN (7-266-042524-3) …

Учебно-методическое пособие подготовлено в соответствии с типовой программой по дисциплине "…" (М…, … г.), на основании рабочей программы (… г.), действующего учебного плана (… г.) и в соответствии с требованиями ГОС ВПО по специальности "Фармация"

Учебно-методическое пособие предназначено для студентов, обучающихся по специальности "Фармация" и является руководством для изучения общего курса высшей математики студентами- заочниками фармацевтического факультета. Оно содержит общие рекомендации студенту- заочнику по работе над курсом высшей математики, программу курса высшей математики, основные теоретические сведения, необходимые для выполнения студентами контрольных работ, методические указания по темам курса с вопросами для самопроверки и контрольные задания.

Рекомендовано в печать Координационным научно-методическим советом и утверждено решением Редакционно-издательского совета ГБОУ ВПО "БГМУ Минздравсоцразвития РФ".

УДК …..

ББК ……

М ………

ISBN (7-266-042524-3) … Ó И.Р. Хайбуллина, О.В. Байгулова

Ó Изд-во ГБОУ ВПО "БГМУ МЗ СР РФ"

СОДЕРЖАНИЕ

	стр.
Предисловие
Общие рекомендации студенту-заочнику по работе над курсом высшей математики
Программа курса "Высшая математика" для студентов фармацевтического факультета
Литература
Методические указания по изучению курса "Высшая математика"
Основные теоретические сведения
Контрольные задания
Правила выполнения и оформления контрольных работ
Номера задач контрольных заданий
Приложения

ПРЕДИСЛОВИЕ

В современной науке и технике математические методы исследования, моделирования и проектирования играют все большую роль. Это обусловлено прежде всего быстрым ростом вычислительной техники, благодаря которой все время существенно расширяются возможности успешного применения математики при решении конкретных задач.

Математика является фундаментальной дисциплиной. Ее преподавание предусматривает:

– развитие логического и алгоритмического мышления;

– овладение основными методами исследования и решения математических задач;

– овладение основными численными методами математики и их простейшими реализациями на ЭВМ;

– выработку умения самостоятельно расширять математические знания.

В настоящее время в системе высшего образования существуют три формы обучения: дневная (или стационарная), вечерняя и заочная. Объем и содержание дисциплин учебного плана той или иной специальности не зависят от формы обучения, но методика их изучения при различных формах обучения различна. В условиях дневной формы обучения содержание курса высшей математики излагается на лекциях; на практических занятиях студенты овладевают основными методами и приемами решения математических задач. Число часов, отводимых на лекции и практические занятия, и составляет объем курса высшей математики для данной специальности.

Настоящее пособие является методическим руководством для изучения общего курса высшей математики студентами- заочниками фармацевтического факультета. Оно содержит общие рекомендации студенту- заочнику по работе над курсом высшей математики, программу курса высшей математики, методические указания по темам курса с вопросами для самопроверки и контрольные задания.

ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ- ЗАОЧНИКУ

Чтение учебника

1. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, производя на бумаге все вычисления (в том числе и те, которые ради краткости опущены в учебнике) и выполняя имеющиеся в учебнике чертежи.

2. Особое внимание следует обращать на определение основных понятий. Студент должен подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно.

3. Необходимо помнить, что каждая теорема состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы.

4. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, формулы, уравнения и т.д. На полях конспекта следует отмечать вопросы, выделенные студентом для получения письменной или устной консультации преподавателя.

5. Письменное оформление работы студента имеет исключительно важное значение. Записи в конспекте должны быть сделаны чисто, аккуратно и расположены в определенном порядке. Хорошее внешнее оформление конспекта по изученному материалу не только приучит студента к необходимому в работе порядку, но и позволит ему избежать многочисленных ошибок, которые происходят из-за небрежных, беспорядочных записей.

6. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой, чтобы при перечитывании конспекта они выделялись и лучше запоминались. Опыт показывает, что многим студентам помогает в работе составление листа, содержащего важнейшие и наиболее часто употребляемые формулы курса. Такой лист не только помогает запомнить формулы, но и может служить постоянным справочником для студента.

Решение задач

1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.

2. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса. Если студент видит несколько путей решения, то он должен сравнить их и выбрать из них самый лучший. Полезно до начала вычислений составить краткий план решения.

3. Решения задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения (например, при графической проверке решения, полученного путем вычислений), то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб.

4. Решение каждой задачи должно доводиться до ответа, требуемого условием, и по возможности в общем виде с выводом формулы. Затем в полученную формулу подставляют числовые значения (если они даны). В промежуточных вычислениях не следует вводить приближенные значения корней, числа % и т.п.

5. Полученный ответ следует проверять способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретным физическим или геометрическим содержанием, то полезно, прежде всего, проверить размерность полученного ответа. Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.

6. Решение задач определенного типа нужно продолжать до приобретения твердых навыков в их решении.

Самопроверка

1. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем. Вопросы для самопроверки, приведенные в настоящем пособии, даны с целью помочь студенту в повторении, закреплении и проверке прочности усвоения изученного материала. В случае необходимости надо еще раз внимательно разобраться в материале учебника, решить ряд задач.

2. Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.

3. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается им как признак усвоения теории. Часто правильное решение задачи получается в результате применения механически заученных формул, без понимания существа дела. Можно сказать, что умение решать задачи является необходимым, но недостаточным условием хорошего знания теории.

Консультации

1. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.), то он может обратиться к преподавателю для получения от него письменной или устной консультации.

2. В своих запросах студент должен точно указать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях, или в доказательстве теоремы, или в выводе формулы по учебнику, то нужно указать, какой это учебник, год его издания и страницу, где рассмотрен затрудняющий его вопрос, и что именно его затрудняет. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения, привести предполагаемый план решения.

3. За консультацией следует обращаться и при сомнении в правильности ответов на вопросы для самопроверки.

Контрольные работы

1. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых - оказать студенту помощь в его работе. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы, на желательное направление дальнейшей работы; помогают сформулировать вопросы для постановки их перед преподавателем.

2. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.

3. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю- рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент нe приобретает необходимых знаний и может оказаться неподготовленным к устному зачету и экзамену.

4. Не рекомендуется присылать в институт одновременно работы по нескольким заданиям: это не дает возможности рецензенту своевременно указать студенту на допущенные им ошибки и удлиняет срок рецензирования работ.

5. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированных контрольных работ студент не допускается к сдаче зачета и экзамена.

6. Распределение контрольных работ по семестрам устанавливается каждым институтом для своих студентов в соответствии с распределением по семестрам материала и сообщается студентам дополнительно.

Зачеты и экзамены

На экзаменах и зачетах выясняется, прежде всего, отчётливое усвоение всех теоретических и практических вопросов программы и умение применять полученные знания к решению практических задач. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела; решение задач в простейших случаях должно выполняться без ошибок и уверенно; всякая письменная и графическая работа должна быть сделана аккуратно и четко. Только при выполнении этих условий знания могут быть признаны удовлетворяющими требованиям, предъявляемым программой.

При подготовке к экзамену учебный материал рекомендуется повторить по учебнику и конспекту.

ПРОГРАММА КУРСА "ВЫСШАЯ МАТЕМАТИКА" ДЛЯ

СТУДЕНТОВ-ЗАОЧНИКОВ ФАРМАЦЕВТИЧЕСКОГО

ФАКУЛЬТЕТА

Дифференциальное исчисление

3. Производная функции, геометрический и механический смысл производной. Непрерывность функции. Задачи, приводящие к понятию производной. Производные высших порядков. Основные правила и формулы дифференцирования. Применение производных к исследованию функций.

6. Дифференциал функции. Функции многих переменных. Частные производные. Частный и полный дифференциал.

Интегральное исчисление

7. Неопределенный интеграл и его основные свойства. Непосредственное интегрирование, интегрирование методом подстановки, интегрирование по частям.

8. Определенный интеграл. Основные свойства определенного интеграла. Связь между определенным интегралом и неопределенным интегралом. Применение определенного интеграла к вычислению площади плоской фигуры и расчету работы переменной силы.

Событие и вероятность

11. Случайные события. Основные виды случайных событий. Определение вероятности.

12. Основные теоремы теории вероятностей: сложения и умножения вероятностей. Формула полной вероятности. Повторные независимые испытания.

Случайные величины

13. Случайные величины (дискретные). Закон распределения дискретной случайной величины.

14. Характеристики распределения дискретных случайных величин.

15. Случайные величины (непрерывные). Функция распределения и плотность распределения вероятностей непрерывной случайной величины, их свойства и вероятностный смысл. Характеристики распределения непрерывных случайных величин.

16. Вероятность попадания в заданный интервал значений непрерывной случайной величины.

Элементы теории корреляции

22. Линейная регрессия, корреляция. Функциональная, статистическая и корреляционная зависимости. Корреляционная таблица. Уравнение линейной регрессии.

23. Выборочные коэффициенты регрессии. Метод наименьших квадратов. Оценка параметров линейной регрессии методом наименьших квадратов.

24. Коэффициент линейной корреляции, его оценка. Понятие о коэффициенте корреляции, его смысл, свойства. Выборочный коэффициент корреляции.

Анализ временных рядов

29. Характеристики дискретных и непрерывных временных рядов. Анализ дискретных временных рядов.

30. Сглаживание временных рядов. Методы сглаживания. Сглаживание временных рядов методом наименьших квадратов, методом скользящего среднего. Прогнозирование временных рядов.

ЛИТЕРАТУРА

1. Лобоцкая Н.Л., Морозов Ю.В., Дунаев А.А. Высшая математика, – Минск, Вышэйшая школа, 1987.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 1970, 1985, т. 1, 2.

3. Задачи и упражнения по математическому анализу для втузов /Под ред. Б.П. Демидовича. – М.: Физматгиз, 1959, 1963; М.: Наука, 1964, 1978.

4. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1980, ч. I- II.

6. Бугров Я.С., Никольский П.С. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука, 1980, 1984.

7. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного – М.: Наука, 1981, 1985.

8. Бугров Я. С., Никольский С. М. Высшая математика. Задачник. – М.: Наука, 1982.

9. Морозов Ю.В. Основы высшей математики статистики. – М.: Медицина, 2004.

10. Баврин И.И. Высшая математика. – М.: Академия, 2006.

11. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшее образование, 2006.

12. Гмурман В.С. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие. М.: Высшее образование, 2005.

13. Вентцель Е.С. Задачи и упражнения по теории вероятностей: учебное пособие. – М.: Академия, 2004.

14. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ: учебник в двух частях. – М.: Проспект, 2007.

15. Основы высшей математики и математической статистики: учебное пособие / Под ред. Ю.М. Смирнова. – М.: Логос, 2005.

16. Павлушков И.В. Основы высшей математики и математической статистики: учебник. – М.: ГЭОТАР-Медиа, 2008. – 424 с.

17. Шапкин А.С. Задачи с решениями по высшей математике, теории вероятности, математической статистике, математическому моделированию: учебное пособие. – М.: Дашков и К^О, 2005.

Функции. Пределы

Литература: [1], гл.1, упр. 1-6, 15-20, 25, 26, 28, 31, 32, 35, 36, 39, 41, 43, 45, 49, 51, 53, 55; [2], гл. II; [3], гл.I, §3.

Вопросы для самопроверки

1. Дайте определение функции. Что называется областью определения функции?

2. Каковы основные способы задания функции? Приведите примеры.

3. Какая функция называется периодической? Приведите примеры.

4. Какая функция называется сложной? Приведите примеры.

5. Какие функции называются элементарными? Приведите примеры.

6. Сформулируйте определение предела функции при стремлении аргумента к некоторому конечному пределу.

7. Сформулируйте определение ограниченной функции.

8. Какая функция называется бесконечно малой и каковы ее основные свойства?

9. Докажите основные теоремы о пределах функций.

10. Сформулируйте "первый замечательный предел".

11. Сформулируйте определение числа е ("второй замечательный предел").

12. Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?

13. Покажите, что при х®0 бесконечно малые sin х, аrcsin х, tg х, аrctg х попарно эквивалентны.

Производная

Литература: [1], гл.2, §2.1-2.5, упр.1, 2, 3, 6, 12, 18, 20, 21, 22, 25, 26, 28, 30, 31, 32, 35, 36, 37, 41, 44, 46, 56, 60; [2], гл. III, §1-4, 9-19, 26, 27.

Можно использовать также [3], гл. II, §1 - 4; [5], ч.I, гл. VII, §1.

Вопросы для самопроверки

1. Сформулируйте определение производной. Каков ее механический и геометрический смысл?

2. Выведите формулы производных суммы, произведения, частного двух функций. Приведите примеры.

3. Напишите формулу дифференцирования сложной функции. Приведите примеры.

4. Выведите формулы производных постоянной и произведения постоянной на функцию.

5. Выведите формулы дифференцирования тригонометрических и логарифмической функций. Приведите примеры.

6. Выведите формулы дифференцирования степенной функции с любым действительным показателем, показательной функции. Приведите примеры.

7. Напишите формулы дифференцирования обратных тригонометрических функций.

Дифференциал

Литература: [1], гл.2, §2.7, упр.85-94, [2], гл. III, §20, 21.

Вопросы для самопроверки

1. Сформулируйте определение дифференциала функции.

2. Для каких функций дифференциал тождественно равен приращению?

3. На чем основано применение дифференциала в приближенных вычислениях?

Вопросы для самопроверки

1. Сформулируйте определения производной и дифференциала высших порядков.

2. Каков механический смысл второй производной?

Функции многих переменных

Литература: [1], гл. 4, упр. 1-5, 11-33.

Вопросы для самопроверки

1. Определение функции двух аргументов.

2. Область определения функции.

3. Способы задания функции.

4. Определение полного приращения функции двух аргументов.

5. Определение частного приращения функции двух аргументов.

6. Определение частной производной первого порядка функции двух аргументов.

7. Частные производные высших порядков.

8. Определение частного дифференциала функции двух аргументов.

9. Определение полного дифференциала функции двух аргументов.

Вопросы для самопроверки

1. Сформулируйте определения возрастающей и убывающей на отрезке функции.

Вопросы для самопроверки

. Сформулируйте определение точки экстремума функции.

. Сформулируйте два правила отыскания экстретумов функции.

. Приведите пример, показывающий, что обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума функции.

. Как найти наибольшее и наименьшее значения функции, дифференцируемой на отрезке? Всегда ли они существуют?

Вопросы для самопроверки

1. Сформулируйте определения выпуклости и вогнутости функции, точек перегиба. Как находятся интервалы выпуклости и вогнутости и точки перегиба функции, заданной уравнением у = f(х)? Приведите примеры.

Асимптоты функции

1. Сформулируйте определение асимптоты функции.

Вопросы для самопроверки

1. Изложите общую схему исследования функции и построения ее графика.

Неопределенный интеграл

Вопросы для самопроверки

1. Дайте определение первообразной функции.

2. Укажите геометрический смысл совокупности первообразных функций. Что называется неопределенным интегралом?

3. Напишите таблицу основных интегралов.

4. Докажите простейшие свойства неопределенного интеграла.

Вопросы для самопроверки

1. Найдите ò(2х – 1)³dх двумя способами: а) непосредственно как интеграл от степенной функции со сложным аргументом; б) раскрыв скобки и проинтегрировав полученную сумму. Покажите, что полученные результаты не противоречат друг другу.

2. Приведите формулу замены переменной в неопределенном интеграле.

3. Выведите формулу интегрирования по частям для неопределенного интеграла. Укажите типы интегралов, вычисление которых целесообразно производить с помощью метода интегрирования по частям.

Определенный интеграл

Литература: [1], гл.6, §6.1-6.6, упр.1, 4, 7, 10, 11, 12, 14, 16, 17, 21, 23, 24, 25, 27, 29, 36, 38, 40, 42, 44, 45, 46, 50; [2], гл. ХI, §1- 6, 8; §7.

Вопросы для самопроверки

1. Дайте определение определенного интеграла и укажите его геометрический смысл.

2. Пусть 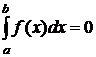, f(х) ¹ 0. Как это истолковать геометрически?

3. Покажите основные свойства определенного интеграла: а) постоянный множитель можно выносить за знак определенного интеграла; б) определенный интеграл от суммы нескольких функций равен сумме определенных интегралов от слагаемых; в) 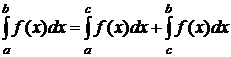, где а < с < b.

4. Докажите теорему о среднем для определенного интеграла и выясните ее геометрический смысл.

5. Докажите, что F(х) = 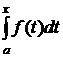является первообразной функцией для функции f(х). Выведите формулу Ньютона-Лейбница для вычисления определенного интеграла.

7. Напишите формулу замены переменной в определенном интеграле. Приведите пример.

8. Напишите формулу интегрирования по частям для определенного интеграла. Приведите пример.

9. Напишите формулу трапеций для приближенного вычисления определенного интеграла. Приведите пример.

Вопросы для самопроверки

1. Дайте определение дифференциального уравнения первого порядка и его общего и частного решения (интеграла). Сформулируйте задачу Коши для дифференциального уравнения первого порядка.

2. Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод нахождения его общего решения. Приведите пример.

3. Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.

4. Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.

Вопросы для самопроверки

1. Изложите метод решения дифференциального уравнения вида

y" = f(x, y'). Приведите пример.

2. Изложите метод решения дифференциального уравнения вида

y" = f(y, y'). Приведите пример.

3. Изложите метод решения дифференциального уравнения вида

y" = f(x). Приведите пример.

4. Напишите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения. Приведите пример.

5. Напишите формулу общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения. Приведите пример.

6. Напишите формулу общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите пример.

3. Составление и решение дифференциальных уравнений на примерах задач физико- химического, фармацевтического и медико- биологического содержания

Литература: [1], гл. 8, упр.1, 6, 7, 14, 15, 19, 20, 21, 22, 23, 24.

Вопросы для самопроверки

1. Составьте и решите дифференциальные уравнения на примере прикладных задач физики.

2. Составьте и решите дифференциальные уравнения на примере прикладных задач химии.

3. Составьте и решите дифференциальные уравнения на примере прикладных задач фармации.

4. Составьте и решите дифференциальные уравнения на примере прикладных задач биологии.

5. Составьте и решите дифференциальные уравнения на примере прикладных задач медицины.

Случайные события

Литература: [1], гл. 9, упр.1-9, 15-18, 21, 24, 28-31; [4], гл. I, §1-3; гл. 2, §4-5; гл. 3, §1-3; гл. 4, §1-3; [2], гл. ХХ, §1-6, 8; [5], ч. II, гл. V, §1-4.

Вопросы для самопроверки

1. Сформулируйте аксиомы теории вероятностей и следствия из них.

2. Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?

3. Дайте определение условной вероятности. Какие события называются независимыми?

4. Дайте определение произведения событий. Докажите теоремы умножения.

5. Сформулируйте формулу полной вероятности.

6. Напишите формулу Байеса.

7. Дайте определение последовательности независимых испытаний, изложите схему Бернулли и напишите формулу Бернулли.

8. Сформулируйте локальную теорему Муавра - Лапласа. Сформулируйте теорему Пуассона. Когда применяются эти теоремы?

Случайные величины

Литература: [1], гл. 10, упр.1-7, 11-15, 20, 22; гл.11, упр.1-6; [4], гл.5, §1-6; гл. 6, §1-5; [2], гл. ХХ, §7, 9-17; [5], ч. II, гл. V, §5, 6, 8-10, 14; [4], гл. 7, §1-6; [5], ч. II, гл. V, §l2,13.

Особое внимание обратите на теоремы, которые позволяют найти вероятность попадания случайной величины в заданный интервал ([1], гл.10, §10.7; [4], гл. V, §2,3; [2], гл. ХХ, §12,13).

Вопросы для самопроверки

1. Дайте определение случайной величины. Приведите примеры.

2. Дайте определение функции распределения случайной величины и докажите ее свойства.

3. Дайте определение плотности распределения вероятностей и докажите ее свойства.

4. Дайте описания дискретных и непрерывных распределений: биномиального, пуассоновского, нормального, равномерного.

5. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному закону?

6. Сформулируйте теоремы о независимых случайных величинах. Что представляет собой распределение суммы независимых случайных величин?

7. Дайте определение математического ожидания случайной величины и докажите его свойства.

8. Дайте определение дисперсии случайной величины и докажите ее свойства.

9. Дайте определение среднего квадратического отклонения случайной величины и укажите его преимущества по сравнению с дисперсией.

10. Напишите неравенство Чебышева. Сформулируйте теорему Чебышева.

11. Что называется характеристическими функциями случайной величины? Сформулируйте их свойства.

12. Сформулируйте центральную предельную теорему и теорему Ляпунова.

Вопросы для самопроверки

1. Что называется выборкой? Напишите формулу для вычисления выборочной средней.

2. Какие оценки называются точечными? Дайте определения несмещенной и состоятельной оценок.

3. Дайте определение выборочной средней, выборочной дисперсии.

4. Какие оценки являются интервальными? В каких случаях следует использовать интервальную оценку?

5. Как найти доверительные интервалы для оценки математического ожидания нормального распределения?

Погрешности измерений

Литература: [1], гл.13, §13.1, 13.3-13.6, упр. 1-11.

Вопросы для самопроверки

1. Что называется истинной абсолютной и истинной относительной погрешностью?

2. Дайте определение систематическим погрешностям. Приведите пример.

3. Дайте определение случайным погрешностям. Приведите пример.

4. Дайте определение промахам. Приведите пример.

5. Что такое равноточные измерения?

6. Что такое прямые и косвенные измерения?

7. Приведите основные формулы нахождения погрешностей прямых измерений.

8. Приведите основные формулы нахождения погрешностей косвенных измерений.

Элементы теории корреляции

Литература: [1], гл. 14, §14.1-14.3, упр. 1, 2, 3.

Вопросы для самопроверки

1. Дайте определение статистической зависимости? Приведите пример.

2. Что называется функциональной зависимостью? Приведите пример.

3. Напишите уравнение регрессии.

4. Что называется линиями регрессии?

5. Как строится корреляционная таблица? Для чего она нужна?

6. Дайте определение коэффициента корреляции. Каковы его свойства?

7. Приведите формулы для вычисления коэффициента линейной корреляции.

Вопросы для самопроверки

1. Дайте определение статистической гипотезы, приведите примеры статистической проверки гипотез.

Основы дисперсионного анализа

Вопросы для самопроверки

1. Дайте определение дисперсионному анализу.

2. Приведите примеры однофакторного и многофакторного дисперсионного анализа.

3. Приведите формулы, лежащие в основе однофакторного дисперсионного анализа при равном числе испытаний на уровнях.

4. Приведите формулы, лежащие в основе однофакторного дисперсионного анализа при неравном числе испытаний на уровнях

Анализ временных рядов

Литература: [1], гл.17, упр.1-9.

Вопросы для самопроверки

1. Дайте определение временного ряда.

2. Дайте определение непрерывного временного ряда.

3. Дайте определение моментного дискретного временного ряда.

4. Дайте определение интервального дискретного временного ряда.

5. Дайте определение случайного временного ряда.

6. Дайте определение детерминированного временного ряда.

7. Перечислите характеристики временного ряда.

8. Напишите формулы вычисления коэффициентов линейного тренда.

9. Выведите формулы вычисления коэффициентов квадратического тренда, используя метод наименьших квадратов.

10. Изложите метод скользящего среднего.

11. Изложите метод взвешенного скользящего среднего.

12. Изложите метод экспоненциального сглаживания.

13. Напишите формулы вычисления коэффициентов уравнения прогноза.

Вопросы для самопроверки

1. Приведите примеры задач линейного программирования.

2. Составьте модель транспортной задачи.

3. Изложите метод северо-западного угла для нахождения базисного решения.

4. Изложите метод потенциалов.

Вопросы для самопроверки

1. Перечислите факторы, характеризующие системы массового обслуживания.

2. Перечислите основные свойства простейшего потока требований.

3. Напишите формулу вычисления вероятности поступления k заявок за время t для простейшего потока.

4. Дайте классификацию систем массового обслуживания.

5. Напишите формулы вычисления характеристик одноканальной системы массового обслуживания с неограниченной очередью.

6. Сформулируйте теорему А.Я. Хинчина.

7. Опишите проверку соответствия потока заявок распределению Пуассона.

Предел функции

Теория пределов позволяет определить характер поведения функции y = f(x) при заданном изменении аргумента x.

Определение. Пусть функция f(x) определена в некоторой окрестности точки x = x₀. Число А называется пределом функции f(x) в точке x₀, если для любого числа e > 0 найдется такое положительное число d, что для любого x ¹ x₀, удовлетворяющего неравенству |x – x₀| < d, выполняется соотношение |f(x) – A| < e. Обозначается: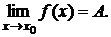

Понятие предела функции дает возможность узнать, к чему стремится значение функции, когда значение аргумента стремится к x₀.

Основные теоремы о пределах

1) Предел постоянной величины равен постоянной величине:

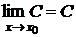
2) Функция f(x) при x ® x₀ не может иметь двух пределов.

3) Предел суммы (или разности) нескольких функций равен сумме (или разности) пределов этих функций, при условии, что они существуют:

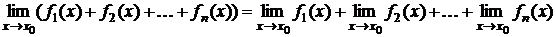
4) Предел произведения нескольких функций равен произведению пределов этих функций, при условии, что они существуют:

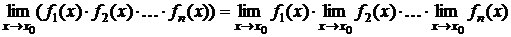
5) Предел отношения двух функций равен отношению пределов этих функций, при условии, что они существуют и предел знаменателя не равен нулю:

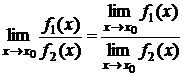
6) Если функция имеет предел при x ® x₀, то:

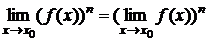
7) Постоянный множитель можно выносить за знак предела:

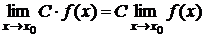
Пример 1.1. Найти предел .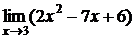

Решение: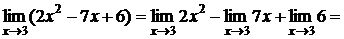

(по свойству 3)

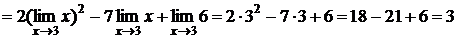
(по свойс- (по свой- (по свой-

твам 6, 7) ству 7) ству 1)

Специальные приемы нахождения пределов

Если функция f(x) в точке x = x₀ не определена, но предел существует, то нужно выполнить ряд преобразований.

1) При вычислении предела частного двух функций при использовании основных свойств пределов получается неопределенность вида 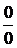. Чтобы от нее избавиться, необходимо преобразовать дробь, умножив числитель и знаменатель на число, сопряженное числителю.

Пример 1.2. Найти предел